正多面体

正多面体（せいためんたい、英: regular polyhedron）、またはプラトン（の）立体（プラトン（の）りったい、英: Platonic solid）^[1]とは、全ての面が互いに合同な正多角形であり、かつ各頂点を含む面の数が等しい凸多面体のことである。正多面体は正四面体、正六面体、正八面体、正十二面体、正二十面体の5種類だけある。

正多面体の構成面を正p角形、頂点に集まる面の数を q として {p, q} のように表すことができる。これをシュレーフリ記号という。シュレーフリ記号は半正多面体（別名：アルキメデスの立体）にも拡張することができる。

三次元空間の中に一つの頂点を取り、その周りに取ることが可能な正多角形の数に関する制限から、正多面体が存在する必要条件が、{3,3}, {3,4}, {3,5}, {4,3}, {5,3} の5種類のみであることを示すことができる。同じことは、オイラーの多面体公式あるいはデカルトの不足角の定理からも示すことができる。

しかし、条件を緩めることによって、正多面体の拡張を考えることができる（参照：星型正多面体、ねじれ正多面体、正平面充填形）。

正多面体の定義

ユークリッド『原論』第13巻で、球に内接する5つの正多面体の構成が論じられ、最後に、「いま述べた五つの図形以外に，等辺等角で互いに等しい図形にかこまれる他の図形はつくられない」^[2]と記述されている。このことから、正多面体とは、

1. 面は互いに合同である
2. 面は正多角形である
3. 全ての頂点は同一球面上にある

という条件を全て満たす多面体である、と理解できる^[3]。

条件3については、1、2を満たす凸多面体であることを前提とすれば、

• 全ての二面角は等しい
• 全ての頂点形は正多角形である
• 全ての立体角は合同
• 全ての頂点に同数の面が集まる

と言い換えることもできる。

また、コクセターは、同心の外接球・中接球・内接球をもつことを正多面体の定義とした。

正多面体の諸量

正多面体の一辺を a とすれば、概略下記となる。

名前と図	構成面	面	辺	頂点	シュレーフリ記号	表面積	体積	内接球半径	中接球半径	外接球半径	二面角
正四面体	正三角形	4	6	4	{3,3}	${\displaystyle {\sqrt {3}}a^{2}}$ ${\displaystyle \simeq 1.732a^{2}}$	${\displaystyle {\frac {\sqrt {2}}{12}}a^{3}}$ ${\displaystyle \simeq 0.118a^{3}}$	${\displaystyle {\frac {1}{\sqrt {24}}}a}$ ${\displaystyle \simeq 0.204a}$	${\displaystyle {\frac {1}{\sqrt {8}}}a}$ ${\displaystyle \simeq 0.354a}$	${\displaystyle {\sqrt {\frac {3}{8}}}a}$ ${\displaystyle \simeq 0.612a}$	${\displaystyle \tan ^{-1}{\sqrt {8}}}$ ${\displaystyle \simeq 70.53^{\circ }}$
正六面体	正方形	6	12	8	{4,3}	${\displaystyle 6a^{2}}$	${\displaystyle a^{3}}$	${\displaystyle 0.5a}$	${\displaystyle {\frac {1}{\sqrt {2}}}a}$ ${\displaystyle \simeq 0.707a}$	${\displaystyle {\frac {\sqrt {3}}{2}}a}$ ${\displaystyle \simeq 0.866a}$	${\displaystyle 90^{\circ }}$
正八面体	正三角形	8	12	6	{3,4}	${\displaystyle 2{\sqrt {3}}a^{2}}$ ${\displaystyle \simeq 3.464a^{2}}$	${\displaystyle {\frac {\sqrt {2}}{3}}a^{3}}$ ${\displaystyle \simeq 0.471a^{3}}$	${\displaystyle {\frac {1}{\sqrt {6}}}a}$ ${\displaystyle \simeq 0.408a}$	${\displaystyle 0.5a}$	${\displaystyle {\frac {1}{\sqrt {2}}}a}$ ${\displaystyle \simeq 0.707a}$	${\displaystyle 2\tan ^{-1}{\sqrt {2}}}$ ${\displaystyle \simeq 109.47^{\circ }}$
正十二面体	正五角形	12	30	20	{5,3}	${\displaystyle 3{\sqrt {25+10{\sqrt {5}}}}a^{2}}$ ${\displaystyle \simeq 20.65a^{2}}$	${\displaystyle {\frac {15+7{\sqrt {5}}}{4}}a^{3}}$ ${\displaystyle \simeq 7.663a^{3}}$	${\displaystyle {\sqrt {\frac {25+11{\sqrt {5}}}{40}}}a}$ ${\displaystyle \simeq 1.114a}$	${\displaystyle {\frac {3+{\sqrt {5}}}{4}}a}$ ${\displaystyle \simeq 1.309a}$	${\displaystyle {\frac {{\sqrt {15}}+{\sqrt {3}}}{4}}a}$ ${\displaystyle \simeq 1.401a}$	${\displaystyle \cos ^{-1}\left(-{\frac {1}{\sqrt {5}}}\right)}$ ${\displaystyle \simeq 116.56^{\circ }}$
正二十面体	正三角形	20	30	12	{3,5}	${\displaystyle 5{\sqrt {3}}a^{2}}$ ${\displaystyle \simeq 8.660a^{2}}$	${\displaystyle {5 \over 12}(3+{\sqrt {5}})a^{3}}$ ${\displaystyle \simeq 2.182a^{3}}$	${\displaystyle {\frac {\sqrt {3}}{12}}\left(3+{\sqrt {5}}\right)a}$ ${\displaystyle \simeq 0.756a}$	${\displaystyle a\cos \left({\frac {\pi }{5}}\right)}$ ${\displaystyle \simeq 0.809a}$	${\displaystyle a\sin \left({\frac {2\pi }{5}}\right)}$ ${\displaystyle \simeq 0.951a}$	${\displaystyle \cos ^{-1}\left(-{\frac {\sqrt {5}}{3}}\right)}$ ${\displaystyle \simeq 138.19^{\circ }}$

相互関係

双対

いずれの正多面体の各面の中心を頂点とする立体もまた正多面体となる。これを正多面体の双対関係といい、3通りの組み合わせが存在する。正四面体同士の双対を特に自己双対という。

組み合わせ	図
正四面体と正四面体	正四面体 ↔ 正四面体
正六面体と正八面体	正六面体 → 正八面体	正八面体 → 正六面体
正十二面体と正二十面体	正十二面体 → 正二十面体	正二十面体 → 正十二面体

正十二面体と正二十面体が同一の球に内接するとき、正十二面体の正五角形と正二十面体の正三角形は同じ円に内接する。

（「５つの正多面体の比較」アリスタイオス、BC320)[1]

また、正六面体と正八面体が同一の球に内接するとき、正六面体の正方形と正八面体の正三角形は同じ円に内接する。

正多面体同士の間には、もれなく内接・外接の関係がある^[4]。

面接触関係

外接する正多面体に対して、内接する正多面体が複数の面を接する関係には次の3通りがある。（　）内に内接正多面体を示す。

• 正四面体（正八面体）
• 正四面体（正二十面体）
• 正八面体（正二十面体）

辺接触関係

外接する正多面体の各面に対して、内接する正多面体の辺が接する関係には次の4通りがある。

• 正六面体（正四面体）
• 正六面体（正十二面体）
• 正六面体（正二十面体）
• 正十二面体（正六面体）

点接触関係

外接する正多面体の各面の面心に対して、内接する正多面体の一部の頂点が接する関係には次の3通りがある。

• 正四面体（正六面体）
• 正四面体（正十二面体）
• 正八面体（正十二面体）

外接する正多面体の一部の面心に対して、内接する正多面体の全ての頂点が接する関係には次の3通りがある。

• 正八面体（正四面体）
• 正二十面体（正四面体）
• 正二十面体（正六面体）

外接する正多面体の一部の辺の中点に対して、内接する正多面体のすべての頂点が接する関係には次の2通りがある。

• 正十二面体（正八面体）
• 正二十面体（正八面体）

外接する正多面体の一部の頂点に対して、内接する正多面体の全ての頂点が接する関係は次の通り。

• 正十二面体（正四面体）

一覧表

正多面体の相互関係を次の表に示す。赤丸は接触点、太線は接触辺、塗り潰し面は接触面である。ただし、裏側は図に描かれていない。

外接＼内接	正四面体	正六面体	正八面体	正十二面体	正二十面体
正四面体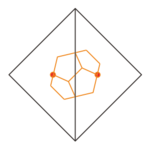
正六面体
正八面体
正十二面体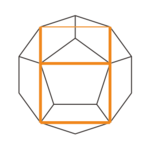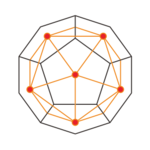
正二十面体

なお、上の表に掲げた外接する正多面体の投影図においては、それらの輪郭は正方形（正四面体の辺中心直投影）、正六角形（正六面体の頂点中心直投影）、正六角形（正八面体の面中心直投影）、正十角形（正十二面体の面中心直投影）、正十角形（正二十面体の頂点中心直投影）と、いずれも正多角形となっている。実際の立体図形においては、その頂点は同一平面にはなく、平行な二平面に一つ置きに属するジグザグ多角形（英語版）であって、正多面体のペトリー多角形 (Petrie polygon) と呼ばれる。

正多面体群

正多面体を自分自身に重ねる三次元空間中の回転操作（回転変換）全体のなす群をいう^[5]。これは三次元回転群の部分群になる。

個々のものは「正何面体群」と呼ぶが、互いに双対の正六面体群と正八面体群、正十二面体群と正二十面体群はそれぞれ群として同じものになるので、後者に代表させて、正四面体群、正八面体群、正二十面体群と呼ぶことが多い。正四面体群は4次交代群A₄、正八面体群は4次対称群S₄、正二十面体群は5次交代群A₅と同型であることが知られている。

シュレーフリ記号を用いて｛p, q｝と書ける正多面体を自分自身に移す回転には次の3つのタイプがある。ただし、正四面体の場合は面の中心と頂点とが相対するので①と②が融合したものと見なす。

• ① 相対する面の中心を結ぶ軸の周りに 2π/p の整数倍回転する操作
• ② 相対する頂点を結ぶ軸の周りに 2π/q の整数倍回転する操作
• ③ 相対する辺の中点を結ぶ軸の周りに π（の整数倍）回転する操作

次の表において、①,②,③には単位元でないものの数を示した。

正多面体の変換群

	p	q	①	②	③	単位元	合計（位数）	2回対称軸	3回対称軸	4回対称軸	5回対称軸
正四面体	3	3	8		3	1	12	3	4	-	-
正六面体	4	3	9	8	6	1	24	6	4	3	-
正八面体	3	4	8	9	6	1	24	6	4	3	-
正十二面体	5	3	24	20	15	1	60	15	10	-	6
正二十面体	3	5	20	24	15	1	60	15	10	-	6

これらの群の位数はさまざまな方法で記述できる。

位数=①の数+②の数+③の数+1

位数=面の数×p

位数=頂点の数×q

位数=1+(2-1)×2回対称軸の数+(3-1)×3回対称軸の数+(4-1)×4回対称軸の数+(5-1)×5回対称軸の数

正多面体の歴史

正多面体 (Platonic solids) という幾何学的概念の成立についての伝承としては、紀元前後のユークリッド『原論』の写本に残された次のようなメモが広く信頼されている。

この第13巻では5個のいわゆるプラトン立体を扱っているが、これはプラトンによるものではない。前述の5個の図形のうち3つ、つまり立方体、正四面体、正十二面体はピタゴラス学派によるものであり、正八面体と正二十面体はテアイテトスによる。プラトンが『ティマイオス』においてこれらに言及したためにプラトンの名前が付いたのである。この巻にユークリッドの名前も載っているのは、かれがこの巻を原論に収録したからである。

鉱物結晶に見られる正多面体

日本産鉱物の結晶の中で正多面体状結晶形態をとることが記録されている主な鉱物種は以下の通り^[6]。

• 正四面体
  • 安四面銅鉱 (Tetrahedrite) などの四面銅鉱グループや閃亜鉛鉱 (Sphalerite)、ズニ石 (Zunyite) など
• 正六面体
  • 黄鉄鉱 (Pyrite)、方鉛鉱 (Galena)、自然銅 (Native copper)、黒辰砂 (Metacinnabar)、蛍石 (Fluorite)、角銀鉱 (Chlorargyrite)、閃マンガン鉱 (Alabandite)、毒鉄鉱 (Pharmacosiderite) など
• 正八面体
  • 黄鉄鉱 (Pyrite)、自然金 (native gold)、自然銅 (Native copper)、ハウエル鉱 (Hauerite)、輝コバルト鉱 (Cobaltite)、蛍石 (Fluorite)、赤銅鉱 (Cuprite)、緑マンガン鉱 (Manganosite)、尖晶石 (Spinel)、磁鉄鉱 (Magnetite)、クロム鉄鉱 (Chromite) など
• （正五角形ではない）五角十二面体
  • 黄鉄鉱 (Pyrite)
• （一部は正三角形ではない）三角二十面体
  • 黄鉄鉱 (Pyrite)

閃亜鉛鉱	黄鉄鉱	尖晶石	黄鉄鉱	黄鉄鉱
正四面体	正六面体	正八面体	五角十二面体	三角二十面体
面指数 {111}	面指数 {100}	面指数 {111}	面指数 {210}	面指数 {111} {210}

正多面体による空間充填

正多面体のみによる空間充填には次の2通りがある。

• 正六面体（立方体）単独
• 正四面体と正八面体による空間充填。構成比は2:1。

正十二面体は単独で空間を埋め尽くすことはできないが、単純立方格子状に配置すると、正六面体とジョンソン立体91番とによって空間充填する^[7]。 構成比は1:1:3。

正二十面体も単独で空間を埋め尽くすことはできないが、単純立方格子状に配置すると、下図の三角二十面体と楔形の黄金四面体（辺の比1:φ）とによって空間充填する。構成比は1:1:6。

正六面体	正四面体 2	正十二面体 1	正二十面体 1
	正八面体 1	正六面体 1	三角二十面体 {1φ0} {111} 1
		ジョンソン立体91番 3	黄金四面体 {1φ0} {111} 6

脚注

関連項目

• 正多角形
• 正多胞体
• ティマイオス

外部リンク

• 正多面体の作り方
• 正多面体の展開図