正十二面体

正十二面体
種別	正多面体、十二面体
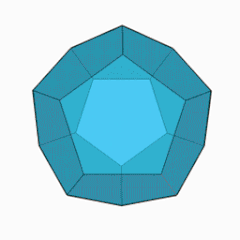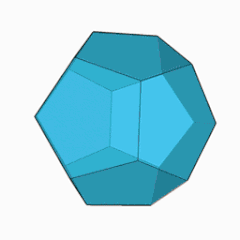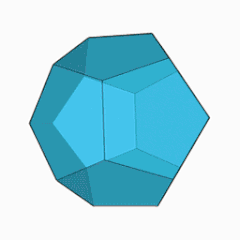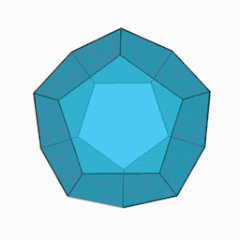
面形状	12枚の正五角形
辺数	30
頂点数	20
頂点形状	53
シュレーフリ記号	{5, 3}
ワイソフ記号	3 | 2 5
対称群	Ih
双対多面体	正二十面体
特性	凸集合
展開図
テンプレートを表示

正十二面体（せいじゅうにめんたい、英: regular dodecahedron）は正多面体の1つ。空間を正五角形12枚で囲んだ凸多面体。

性質

• ねじれ双五角錐の両頭頂点を切った立体（Truncated pentagonal trapezohedron）の、特殊な形。
• 向かい合う面は平行である。
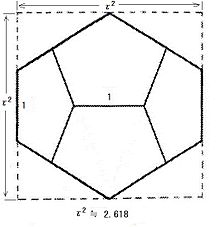
• 正十二面体の一辺と外接立方体の一辺の比はおよそ 1 : 2.618
• 二面角 116.56505° = arccos(−1/√5)
• 展開図の数は43380種類。
• 面の数は12、辺の数は30、頂点の数は20。
• 頂点形状は正三角錐であり、3本の辺と3枚の正五角形が集まる。これらはパスカルの三角形の第4段の2、3番目の数字に等しい。
• 正二十面体と双対である。

計量

面の面積	${\displaystyle A={1 \over 4}{\sqrt {25+10{\sqrt {5}}}}\,a^{2}}$	${\displaystyle A={1 \over 4}{\sqrt {5(4\phi +3)}}\,a^{2}}$
表面積	${\displaystyle S=12A=3{\sqrt {25+10{\sqrt {5}}}}\,a^{2}}$	${\displaystyle S=12A=3{\sqrt {5(4\phi +3)}}\,a^{2}}$
体積	${\displaystyle V={\frac {1}{3}}Sr={1 \over 4}(15+7{\sqrt {5}})a^{3}}$	${\displaystyle V={\frac {1}{3}}Sr={1 \over 2}(7\phi +4)a^{3}}$
最長対角線の長さ	${\displaystyle d={1 \over 2}{({\sqrt {15}}+{\sqrt {3}})a}}$	${\displaystyle d={{\sqrt {3}}\phi }a}$
外接球半径	${\displaystyle R={\frac {d}{2}}={1 \over 4}{({\sqrt {15}}+{\sqrt {3}})a}}$	${\displaystyle R={1 \over 2}{{\sqrt {3}}\phi }a}$
内接球半径	${\displaystyle r={\sqrt {25+11{\sqrt {5}} \over 40}}\,a}$	${\displaystyle r={3\phi +2 \over 2{\sqrt {4\phi +3}}}a}$

頂点、辺、面の座標

以下は、標準的な座標の取り方の一つである。ここで ${\displaystyle \phi }$ は黄金比 ${\displaystyle {\frac {1+{\sqrt {5}}}{2}}}$ 、 ${\displaystyle \epsilon _{1},\epsilon _{2},\epsilon _{3}=\pm 1}$ である。

20個の頂点（原点からの距離 ${\displaystyle {\sqrt {3}}}$）の座標

• ${\displaystyle (\epsilon _{1},\epsilon _{2},\epsilon _{3})}$ の8個
• ${\displaystyle (0,\epsilon _{2}\phi ,\epsilon _{3}\phi ^{-1})}$ のxyz座標を偶置換した 12個

30個の辺（長さ${\displaystyle 2\phi ^{-1}}$）の、両端点および中心の座標

• 両端点 ${\displaystyle (\epsilon _{1},\epsilon _{2},\epsilon _{3})}$と${\displaystyle (0,\epsilon _{2}\phi ,\epsilon _{3}\phi ^{-1})}$、中心 ${\displaystyle {\frac {1}{2}}(\epsilon _{1},\epsilon _{2}\phi ^{2},\epsilon _{3}\phi )}$ のxyz座標を偶置換した 24個
• 両端点 ${\displaystyle (0,\epsilon _{2}\phi ,\phi ^{-1})}$と${\displaystyle (0,\epsilon _{2}\phi ,-\phi ^{-1})}$、中心${\displaystyle (0,\epsilon _{2}\phi ,0)}$ のxyz座標を偶置換した 6組

12個の面の、反時計回りの頂点および中心の座標

• 頂点 ${\displaystyle (0,\epsilon _{2}\phi ,\epsilon _{3}\phi ^{-1})}$, ${\displaystyle (-\epsilon _{2}\epsilon _{3},\epsilon _{2},\epsilon _{3})}$, ${\displaystyle (-\epsilon _{2}\epsilon _{3}\phi ^{-1},0,\epsilon _{3}\phi )}$, ${\displaystyle (\epsilon _{2}\epsilon _{3}\phi ^{-1},0,\epsilon _{3}\phi )}$, ${\displaystyle (\epsilon _{2}\epsilon _{3},\epsilon _{2},\epsilon _{3})}$、中心 ${\displaystyle {\frac {\phi +2}{5}}(0,\epsilon _{2},\epsilon _{3}\phi )}$ のxyz座標を偶置換した 12個

正十二面体の作り方

• 正十二面体を内接立方体から構成する方法がユークリッドの『原論』第13巻に記されている。一松信はこれを「立方体に屋根をかける」方法と呼んでいる。^[1]
• これとは逆に、正十二面体を外接立方体から立方体の12の稜を一様に切稜して作る方法が、『多面体木工（増補版）』（佐藤郁郎・中川宏）によって示された。^[2]それは、正十二面体の投影図（辺心図）が、直交する3方向に現れることに基づいている。投影図は100ミリの立方体から切り取る部分の寸法を示しているが、これは黄金比にあたる。切り取る三角形の赤丸の角度が切稜の角度になる。約31.7度である。

立方体から正十二面体を作る様子

発泡スチロールカッターを使って立方体から正十二面体を作る様子を示す。

X軸まわりの切稜

Y軸まわりの切稜

Z軸まわりの切稜

立方体切稜による正十二面体の完成

正十二面体の証明

『ユークリッド原論』第13巻の定理17においては、立方体の一辺を対角線の一つとする五角形のひさしをかけることによって、この五角形が等辺にして一平面上にありかつ等角であることが証明されている^[3]。

正十二面体をつくり，先の図形のように球によってかこみ，そして正十二面体の辺が余線分とよばれる無理線分であることを証明すること。 — 『ユークリッド原論』第13巻の定理17^[4]

図に示したように、『ユークリッド原論』第13巻の定理17の説明^[3]にあるギリシア文字をラテン文字に変更して述べると以下のようになる。

　先に述べた立方体の互いに垂直な二つの面 ABCD､CBEF が定められ､辺 AB，BC，CD，DA，EF，EB，FC のおのおのが G，H，K，L，M，N，O において2等分され，GK HL，MH，NO が結ばれ，NP，PG，HQ のおのおのが点 R，S，T において外中比に分けられ，RP，PS，TQ がそれらの大きい部分とされ，点 R，S，T から立方体の面に垂直に立方体の外側の方向に RU，SV，TW が立てられ，RP，PS，TQ に等しくされ，UB，BW，WC，CV，VU が結ばれたとせよ。五角形 EBWCV は等辺にして一平面上にありかつ等角であると主張する。 — 『ユークリッド原論』第13巻の定理17^[5]

星型 

小星型十二面体 B

大十二面体 C

大星型十二面体 D

この図形を枠に持つ立体

大星型十二面体	小二重三角二十・十二面体	大二重三角二十・十二面体	二重三角十二・十二面体
5個の立方体による複合多面体	5個の正四面体による複合多面体	10個の正四面体による複合多面体

派生的な立体

切頂十二面体 t{5, 3}

二十・十二面体 r{5, 3}

変形十二面体 sr{5, 3}

五方十二面体

正十二面体と正二十面体による複合多面体

近縁となるジョンソンの立体

側錐十二面体

双側錐十二面体

二側錐十二面体

三側錐十二面体

古代の遺物に見られる正十二面体

おそらく日本最古と思われる正十二面体構造を持つ人工物は、５～６世紀ごろの古墳の副葬品の耳飾りに見出すことができる。同じ大きさの銀製や金銅製の環１２個を均等に配置した中空の籠形で、垂らすタイプの耳飾りの中間に用いられた。これまでに、群馬県の梁瀬二子塚古墳、千葉県の祇園大塚山古墳、長野県の畦地一号墳、和歌山県の大谷古墳、奈良県の新沢千塚から出土した遺物に確認されている。全く同じではないが似たような構造を持つ耳飾りは朝鮮半島の遺物でも確認されている。^[6]

関連項目

脚注

参考文献

• 小笠英志『4次元以上の空間が見える』ベレ出版、2006年5月25日。ISBN 4-86064-118-3。http://www.beret.co.jp/books/detail/233。  - pp.97-101に正十二面体の対角線の長さを全て求める方法が載っている。
• 一松信『正多面体を解く』東海大学出版会、2002年5月20日。
• 佐藤郁郎、中川宏『多面体木工』（増補版）科学協力学際センター、2011年3月。ISBN 978-4-9905880-0-7。http://torito.jp/shopping/_tamentaimokko.shtml。 
• ハイベア、メンゲ 編『ユークリッド原論』中村幸四郎・寺阪英孝・伊東俊太郎・池田美恵訳・解説、共立出版。  - 全13巻の最初の邦訳。
  • （ハードカバー）1971年7月。ISBN 4-320-01072-8
    • （抜粋）『世界の名著9』 池田美恵訳 中央公論社 1972年
  • （縮刷版）1996年6月。ISBN 4-320-01513-4
  • （追補版）2011年5月。ISBN 978-4-320-01965-2

外部リンク

• 発泡スチロールの立方体から正十二面体をつくろう
• ユークリッド「原論」における正１２面体の証明
• 『正12面体のいろいろな計算（対角線・表面積・体積・内接球・外接球）』 - 高校数学の美しい物語
• Weisstein, Eric W. "Regular Dodecahedron". mathworld.wolfram.com (英語).
• Weisstein, Eric W. "Dodecahedral Graph". mathworld.wolfram.com (英語).

ウィキメディア・コモンズには、十二面体に関連するカテゴリがあります。

表 話 編 歴 多面体
一様多面体	正多面体 正四面体 正六面体 正八面体 正十二面体 正二十面体 半正多面体 切頂四面体 切頂六面体 切頂八面体 切頂十二面体 切頂二十面体 立方八面体 二十・十二面体 斜方立方八面体 斜方二十・十二面体 斜方切頂立方八面体 斜方切頂二十・十二面体 変形立方体 変形十二面体 星型正多面体 小星型十二面体 大十二面体 大星型十二面体 大二十面体 その他 八面半八面体 四面半六面体 小立方立方八面体 大立方立方八面体 立方半八面体 立方切頂立方八面体 一様大斜方立方八面体 小斜方六面体 星型切頂六面体 大切頂立方八面体 大斜方六面体 小二重三角二十・十二面体 小二十・二十・十二面体 小変形二十・二十・十二面体 小十二・二十・十二面体 十二・十二面体 切頂大十二面体 斜方十二・十二面体 小斜方十二面体 変形十二・十二面体 二重三角十二・十二面体 大二重三角十二・二十・十二面体 小二重三角十二・二十・十二面体 二十・十二・十二面体 二十面切頂十二・十二面体 変形二十・十二・十二面体 大二重三角二十・十二面体 大二十・二十・十二面体 小二十面半十二面体 小十二・二十面体 小十二面半十二面体 大二十・十二面体 切頂大二十面体 斜方二十面体 大変形二十・十二面体 小星型切頂十二面体 切頂十二・十二面体 逆変形十二・十二面体 大十二・二十・十二面体 小十二面半二十面体 大十二・二十面体 大変形十二・二十・十二面体 大十二面半二十面体 大星型切頂十二面体 一様大斜方二十・十二面体 大切頂二十・十二面体 大逆変形二十・十二面体 大十二面半十二面体 大二十面半十二面体 小反屈変形二十・二十・十二面体 大斜方十二面体 大反屈変形二十・十二面体 大二重斜方二十・十二面体
カタランの立体	三方四面体 三方八面体 四方六面体 三方二十面体 五方十二面体 菱形十二面体 菱形三十面体 凧形二十四面体 凧形六十面体 六方八面体 六方二十面体 五角二十四面体 五角六十面体
ジョンソンの立体	正四角錐 正五角錐 正三角台塔 正四角台塔 正五角台塔 正五角丸塔 正三角錐柱 正四角錐柱 正五角錐柱 正四角錐反柱 正五角錐反柱 双三角錐 双五角錐 双三角錐柱 双四角錐柱 双五角錐柱 双四角錐反柱 正三角台塔柱 正四角台塔柱 正五角台塔柱 正五角丸塔柱 正三角台塔反柱 正四角台塔反柱 正五角台塔反柱 正五角丸塔反柱 異相双三角柱 同相双三角台塔 同相双四角台塔 異相双四角台塔 同相双五角台塔 異相双五角台塔 同相五角台塔丸塔 異相五角台塔丸塔 同相双五角丸塔 同相双三角台塔柱 異相双三角台塔柱 異相双四角台塔柱 同相双五角台塔柱 異相双五角台塔柱 同相五角台塔丸塔柱 異相五角台塔丸塔柱 同相双五角丸塔柱 異相双五角丸塔柱 双三角台塔反柱 双四角台塔反柱 双五角台塔反柱 五角台塔丸塔反柱 双五角丸塔反柱 側錐三角柱 二側錐三角柱 三側錐三角柱 側錐五角柱 二側錐五角柱 側錐六角柱 双側錐六角柱 二側錐六角柱 三側錐六角柱 側錐十二面体 双側錐十二面体 二側錐十二面体 三側錐十二面体 二側錐欠損二十面体 三側錐欠損二十面体 側錐三側錐欠損二十面体 側台塔切頂四面体 側台塔切頂立方体 双側台塔切頂立方体 側台塔切頂十二面体 双側台塔切頂十二面体 二側台塔切頂十二面体 三側台塔切頂十二面体 側台塔回転斜方二十・十二面体 双側台塔回転斜方二十・十二面体 二側台塔回転斜方二十・十二面体 三側台塔回転斜方二十・十二面体 側台塔欠損斜方二十・十二面体 双側台塔回転欠損斜方二十・十二面体 二側台塔回転欠損斜方二十・十二面体 二側台塔回転側台塔欠損斜方二十・十二面体 双側台塔欠損斜方二十・十二面体 二側台塔欠損斜方二十・十二面体 側台塔回転二側台塔欠損斜方二十・十二面体 三側台塔欠損斜方二十・十二面体 変形双五角錐 変形四角反柱 球形屋根 側錐球形屋根 長球形屋根 広底長球形屋根 五角錐球形屋根 双三日月双丸塔 三角広底球形屋根丸塔
ゾーン多面体	平行六面体 菱形十二面体第2種 菱形二十面体 菱形九十面体 長菱形十二面体
星型多面体	小三角六辺形二十面体 完全二十面体 星型八面体
ねじれ正多面体	四角六片四角孔ねじれ正多面体 六角四片四角孔ねじれ正多面体 六角六片三角孔ねじれ正多面体
面の数による分類	二面体 四面体 五面体 六面体 七面体 八面体 十面体 十二面体 十四面体 二十面体 二十四面体 三十面体 四十八面体 六十面体 百二十面体
その他	角錐 角柱 双角錐 反角柱 ねじれ双角錐 プリズマトイド（英語版） 擬大斜方立方八面体 大二重変形二重斜方十二面体 切稜立方体 穿孔多面体 ダ・ヴィンチの星 正四面体リング 凸多面体 凹多面体 双対多面体 複合多面体 平面充填形