Gompertz distribution

Gompertz distribution

Probability density function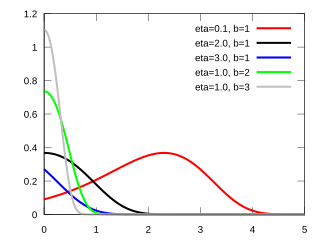
Cumulative distribution function
Parameters	shape ${\displaystyle \eta >0\,\!}$, scale ${\displaystyle b>0\,\!}$
Support	${\displaystyle x\in [0,\infty )\!}$
PDF	${\displaystyle b\eta \exp \left(\eta +bx-\eta e^{bx}\right)}$
CDF	${\displaystyle 1-\exp \left(-\eta \left(e^{bx}-1\right)\right)}$
Quantile	${\displaystyle {\frac {1}{b}}\ln \left(1-{\frac {1}{\eta }}\ln(1-u)\right)}$
Mean	${\displaystyle (1/b)e^{\eta }{\text{Ei}}\left(-\eta \right)}$ ${\displaystyle {\text{where Ei}}\left(z\right)=\int \limits _{-z}^{\infty }\left(e^{-v}/v\right)dv}$
Median	${\displaystyle \left(1/b\right)\ln \left[\left(1/\eta \right)\ln \left(1/2\right)+1\right]}$
Mode	${\displaystyle =\left(1/b\right)\ln \left(1/\eta \right)\ }$ ${\displaystyle {\text{with }}0<{\text{F}}\left(x^{*}\right)<1-e^{-1}=0.632121,0<\eta <1}$ ${\displaystyle =0,\quad \eta \geq 1}$
Variance	${\displaystyle \left(1/b\right)^{2}e^{\eta }\{-2\eta {\ }_{3}{\text{F}}_{3}\left(1,1,1;2,2,2;\eta \right)+\gamma ^{2}}$${\displaystyle +\left(\pi ^{2}/6\right)+2\gamma \ln \left(\eta \right)+[\ln \left(\eta \right)]^{2}-e^{\eta }[{\text{Ei}}\left(-\eta \right)]^{2}\}}$ ${\displaystyle {\begin{aligned}{\text{ where }}&\gamma {\text{ is the Euler constant: }}\,\!\\&\gamma =-\psi \left(1\right)={\text{0.577215... }}\end{aligned}}}$${\displaystyle {\begin{aligned}{\text{ and }}{}_{3}{\text{F}}_{3}&\left(1,1,1;2,2,2;-z\right)=\\&\sum _{k=0}^{\infty }\left[1/\left(k+1\right)^{3}\right]\left(-1\right)^{k}\left(z^{k}/k!\right)\end{aligned}}}$
MGF	${\displaystyle {\text{E}}\left(e^{-tx}\right)=\eta e^{\eta }{\text{E}}_{t/b}\left(\eta \right)}$ ${\displaystyle {\text{with E}}_{t/b}\left(\eta \right)=\int _{1}^{\infty }e^{-\eta v}v^{-t/b}dv,\ t>0}$

In probability and statistics, the Gompertz distribution is a continuous probability distribution, named after Benjamin Gompertz. The Gompertz distribution is often applied to describe the distribution of adult lifespans by demographers^[1][2] and actuaries.^[3][4] Related fields of science such as biology^[5] and gerontology^[6] also considered the Gompertz distribution for the analysis of survival. More recently, computer scientists have also started to model the failure rates of computer code by the Gompertz distribution.^[7] In Marketing Science, it has been used as an individual-level simulation for customer lifetime value modeling.^[8] In network theory, particularly the Erdős–Rényi model, the walk length of a random self-avoiding walk (SAW) is distributed according to the Gompertz distribution.^[9]

Specification

Probability density function

The probability density function of the Gompertz distribution is:

${\displaystyle f\left(x;\eta ,b\right)=b\eta \exp \left(\eta +bx-\eta e^{bx}\right){\text{for }}x\geq 0,\,}$

where ${\displaystyle b>0\,\!}$ is the scale parameter and ${\displaystyle \eta >0\,\!}$ is the shape parameter of the Gompertz distribution. In the actuarial and biological sciences and in demography, the Gompertz distribution is parametrized slightly differently (Gompertz–Makeham law of mortality).

Cumulative distribution function

The cumulative distribution function of the Gompertz distribution is:

${\displaystyle F\left(x;\eta ,b\right)=1-\exp \left(-\eta \left(e^{bx}-1\right)\right),}$

where ${\displaystyle \eta ,b>0,}$ and ${\displaystyle x\geq 0\,.}$

Moment generating function

The moment generating function is:

${\displaystyle {\text{E}}\left(e^{-tX}\right)=\eta e^{\eta }{\text{E}}_{t/b}\left(\eta \right)}$

where

${\displaystyle {\text{E}}_{t/b}\left(\eta \right)=\int _{1}^{\infty }e^{-\eta v}v^{-t/b}dv,\ t>0.}$

Properties

The Gompertz distribution is a flexible distribution that can be skewed to the right and to the left. Its hazard function ${\displaystyle h(x)=\eta be^{bx}}$ is a convex function of ${\displaystyle F\left(x;\eta ,b\right)}$. The model can be fitted into the innovation-imitation paradigm with ${\displaystyle p=\eta b}$ as the coefficient of innovation and ${\displaystyle b}$ as the coefficient of imitation. When ${\displaystyle t}$ becomes large, ${\displaystyle z(t)}$ approaches ${\displaystyle \infty }$. The model can also belong to the propensity-to-adopt paradigm with ${\displaystyle \eta }$ as the propensity to adopt and ${\displaystyle b}$ as the overall appeal of the new offering.

Shapes

The Gompertz density function can take on different shapes depending on the values of the shape parameter ${\displaystyle \eta \,\!}$:

• When ${\displaystyle \eta \geq 1,\,}$ the probability density function has its mode at 0.
• When ${\displaystyle 0<\eta <1,\,}$ the probability density function has its mode at

${\displaystyle x^{*}=\left(1/b\right)\ln \left(1/\eta \right){\text{with }}0<F\left(x^{*}\right)<1-e^{-1}=0.632121}$

Kullback-Leibler divergence

If ${\displaystyle f_{1}}$ and ${\displaystyle f_{2}}$ are the probability density functions of two Gompertz distributions, then their Kullback-Leibler divergence is given by

${\displaystyle {\begin{aligned}D_{KL}(f_{1}\parallel f_{2})&=\int _{0}^{\infty }f_{1}(x;b_{1},\eta _{1})\,\ln {\frac {f_{1}(x;b_{1},\eta _{1})}{f_{2}(x;b_{2},\eta _{2})}}dx\\&=\ln {\frac {e^{\eta _{1}}\,b_{1}\,\eta _{1}}{e^{\eta _{2}}\,b_{2}\,\eta _{2}}}+e^{\eta _{1}}\left[\left({\frac {b_{2}}{b_{1}}}-1\right)\,\operatorname {Ei} (-\eta _{1})+{\frac {\eta _{2}}{\eta _{1}^{\frac {b_{2}}{b_{1}}}}}\,\Gamma \left({\frac {b_{2}}{b_{1}}}+1,\eta _{1}\right)\right]-(\eta _{1}+1)\end{aligned}}}$

where ${\displaystyle \operatorname {Ei} (\cdot )}$ denotes the exponential integral and ${\displaystyle \Gamma (\cdot ,\cdot )}$ is the upper incomplete gamma function.^[10]

Related distributions

• If X is defined to be the result of sampling from a Gumbel distribution until a negative value Y is produced, and setting X=−Y, then X has a Gompertz distribution.
• The gamma distribution is a natural conjugate prior to a Gompertz likelihood with known scale parameter ${\displaystyle b\,\!.}$^[8]
• When ${\displaystyle \eta \,\!}$ varies according to a gamma distribution with shape parameter ${\displaystyle \alpha \,\!}$ and scale parameter ${\displaystyle \beta \,\!}$ (mean = ${\displaystyle \alpha /\beta \,\!}$), the distribution of ${\displaystyle x}$ is Gamma/Gompertz.^[8]

• If ${\displaystyle Y\sim \mathrm {Gompertz} }$, then ${\displaystyle X=\exp(Y)\sim \mathrm {Weibull} ^{-1}}$, and hence ${\displaystyle \exp(-Y)\sim \mathrm {Weibull} }$.^[12]

Applications

• In hydrology the Gompertz distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges. The blue picture illustrates an example of fitting the Gompertz distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution. The rainfall data are represented by plotting positions as part of the cumulative frequency analysis.

See also

• Gompertz-Makeham law of mortality
• Gompertz function
• Customer lifetime value
• Gamma Gompertz distribution

Notes

References

• Bemmaor, Albert C.; Glady, Nicolas (2011). "Implementing the Gamma/Gompertz/NBD Model in MATLAB" (PDF). Cergy-Pontoise: ESSEC Business School.^{[permanent dead link]}
• Gompertz, B. (1825). "On the Nature of the Function Expressive of the Law of Human Mortality, and on a New Mode of Determining the Value of Life Contingencies". Philosophical Transactions of the Royal Society of London. 115: 513–583. doi:10.1098/rstl.1825.0026. JSTOR 107756. S2CID 145157003.
• Johnson, Norman L.; Kotz, Samuel; Balakrishnan, N. (1995). Continuous Univariate Distributions. Vol. 2 (2nd ed.). New York: John Wiley & Sons. pp. 25–26. ISBN 0-471-58494-0.
• Sheikh, A. K.; Boah, J. K.; Younas, M. (1989). "Truncated Extreme Value Model for Pipeline Reliability". Reliability Engineering and System Safety. 25 (1): 1–14. doi:10.1016/0951-8320(89)90020-3.