Simplexe

Pour les articles homonymes, voir Simplexe (homonymie).

En mathématiques, et plus particulièrement en géométrie, un simplexe est une généralisation du triangle à une dimension quelconque.
Définition

En géométrie, un simplexe ou n-simplexe est l'analogue à n dimensions du triangle. Il doit son nom au fait que c'est l'objet géométrique clos le « plus simple » qui ait n dimensions. Par exemple sur une droite (1 dimension) l'objet le plus simple à 1 dimension est le segment, alors que dans le plan (2 dimensions) l'objet géométrique clos le plus simple à 2 dimensions est le triangle, et dans l'espace (3 dimensions) l'objet géométrique clos le plus simple à 3 dimensions est le tétraèdre (pyramide à base triangulaire).
Plus exactement, un simplexe est l'enveloppe convexe d'un ensemble de (n+1) points utilisé pour former un repère affine dans un espace affine de dimension n, ce qui signifie que :
- sur une droite le repère sera fait d'une origine et de 1 point (généralement un repère (O, I), définissant l'unité de l'axe), et [OI] est un segment.
- dans le plan le repère sera fait d'une origine et de 2 points (généralement un repère (O, I, J), définissant l'unité pour chaque axe), et OIJ est un triangle.
- dans l'espace le repère sera fait d'une origine et de 3 points (généralement un repère (O, I, J, K), définissant l'unité pour chaque axe), et OIJK est un tétraèdre.
Les coordonnées des sommets du simplexe (dans le repère formé de ses sommets) sont alors :
- e0 = (0, 0, 0, …, 0),
- e1 = (1, 0, 0, …, 0),
- e2 = (0, 1, 0, …, 0),
- en = (0, 0, 0, …, 1)
Cependant, par souci de symétrie entre les sommets, on préfère souvent plonger le simplexe dans un hyperplan affine de l'espace de dimension n+1, en attribuant à chaque sommet les n + 1 coordonnées suivantes :
- e0 = (1, 0, 0, 0, …, 0),
- e1 = (0, 1, 0, 0, …, 0),
- e2 = (0, 0, 1, 0, …, 0),
- en = (0, 0, 0, 0, …, 1)
Le nombre n est appelé la dimension ou le degré ou même l'ordre du n-simplexe s. Par exemple, un 0-simplexe est un point, un 1-simplexe est un segment, un 2-simplexe est un triangle, un 3-simplexe est un tétraèdre, un 4-simplexe est un pentachore (ou pentatope), etc. Comme le simplexe à 0 dimension est un singleton, on attribue parfois à l'ensemble vide la dimension –1.
Soit donc s un simplexe formé par les points a0..., an. Un point x de s s'écrit de manière unique :
où les ti sont les coordonnées barycentriques positives ou nulles de x relatives à a0..., an. On remarque la ressemblance entre cette formule et celle de l'équilibre d'un objet en physique mécanique statique : , qui dit que la somme des forces extérieures appliquées à un objet en équilibre est égale au vecteur nul. Cela vient du fait que l'objet, quel que soit l'intensité de ces n forces qui le tirent (qu'on peut se représenter comme n ressorts attachés à l'objet et aux n sommets d'un (n – 1)-simplexe), restera toujours dans ce simplexe : tout point du simplexe peut être défini par ces forces qui l'attirent plus ou moins vers tel ou tel sommet, d'où l'utilisation de la notion de barycentre. On notera de plus que, pour qu'un objet soit en équilibre, il doit nécessairement se trouver dans le simplexe formé par les points qui l'attirent.
Un simplexe régulier est un simplexe qui est aussi un polytope régulier (c'est-à-dire que toutes ses arêtes sont de même longueur, que ses faces sont de même nature géométrique, et s'organisent de la même façon dans les mêmes quantités à chaque sommet).
Le mot « simplexe » a été donné par Pieter Hendrik Schoute en 1902, mais Ludwig Schläfli avait déjà démontré l'existence des simplexes réguliers pour toute dimension n (donc des simplexes tout court) lorsqu'il a prouvé qu'il y avait toujours au moins trois polytopes réguliers pour toute dimension supérieure à 3 (à savoir le n-simplexe, ainsi que le n-hypercube et le n-hyperoctaèdre).
Éléments
Les éléments d'un simplexe sont appelés n-faces, où n est leur dimension :
- les 0-faces sont appelées sommets
- les 1-faces sont appelées arêtes
- les 2-faces sont appelées faces
- les 3-faces sont appelées cellules
Les (n – 1)-faces d'un n-simplexe forment son enveloppe.
Les n-faces d'un simplexe sont elles-mêmes des simplexes de dimensions inférieures. Par exemple, un tétraèdre a des faces triangulaires.
Quand on liste les n-faces des simplexes ainsi que leur nombre, on obtient un triangle de Pascal :
| Simplexe | Nombre de sommets | Nombre d'arêtes | Nombre de faces | Nombre de cellules | Nombre de 4-faces | Nombre de 5-faces | Nombre de 6-faces |
|---|---|---|---|---|---|---|---|
| Point | 1 | - | - | - | - | - | - |
| Segment | 2 | 1 | - | - | - | - | - |
| Triangle | 3 | 3 | 1 | - | - | - | - |
| Tétraèdre | 4 | 6 | 4 | 1 | - | - | - |
| Pentachore | 5 | 10 | 10 | 5 | 1 | - | - |
| 5 simplexe | 6 | 15 | 20 | 15 | 6 | 1 | - |
| 6 simplexe | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
| … |
Triangle de Pascal, dont une des caractéristiques est que la seconde colonne corresponde à chaque nombre triangulaire, la troisième à chaque nombre tétraédrique, la quatrième à chaque nombre pentatopique…
Le nombre de sommets d'un n-simplexe vaut , et le nombre de n-faces vaut toujours car il s'agit du simplexe lui-même. Le nombre d'arêtes d'un n-simplexe vaut , car il s'agit du nombre de couples de sommets différents que l'on peut réaliser.
Entre les nombres de chaque élément d'un simplexe, il y a une relation d'Euler dans laquelle, en ajoutant les éléments de dimension paire (sommets, faces, 4-faces, 6-faces…) et en retranchant les éléments de dimension impaire (arêtes, cellules, 5-faces, 7-faces…), on obtient la caractéristique d'Euler-Poincaré du simplexe, qui vaut 0 pour les simplexes de degré pair et 2 pour les simplexes de degré impair :
, où est le nombre de (n – 1)-faces (on utilise n – 1 dans la formule au lieu de n pour ne pas compter le n-simplexe lui-même et s'arrêter à ses éléments stricts).
- Pour le segment : 2 points = 2
- Pour le triangle : 3 points - 3 arêtes = 0
- Pour le tétraèdre : 4 points - 6 arêtes + 4 faces = 2
- Pour le pentachore : 5 points - 10 arêtes + 10 faces - 5 cellules = 0
Représentations

Les n-simplexes ayant souvent plus de dimensions que les objets que nous sommes habitués à voir dans la vie courante, on utilise différents moyens de représentation pour travailler plus facilement avec. Parmi ces représentations, on utilise souvent les projections d'un n-simplexe dans un espace dimension inférieure (généralement 2 ou 3).
Il est impossible de représenter parfaitement un objet dans un espace qui a moins de dimensions que lui, donc il faut utiliser ces représentations avec prudence, certaines déforment les longueurs, les angles, voire la structure du simplexe, ou alors nous font voir des segments qui se croisent alors qu'en réalité ils ne se croisent pas.
Graphes
La représentation en deux dimensions d'un n-simplexe est un graphe complet. Pour tracer le graphe d'un n-simplexe, il suffit de relier tous entre eux n + 1 points.
Quand on a affaire au graphe d'un simplexe dont on ne connaît pas le degré, il suffit de compter le nombre de segments qui sont reliés à un sommet.
Pour passer du graphe d'un n-simplexe à celui d'un (n + 1)-simplexe, on ajoute un nouveau point et on relie tous les autres à celui-ci.
| Simplexe | Segment | Triangle | Tétraèdre | Pentatope | 5 simplexe | 6 simplexe | 7 simplexe |
|---|---|---|---|---|---|---|---|
| Dimension | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Sommets | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Graphe |  |  | 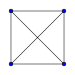 |  |  |  |  |
Attention : le graphe n'étant qu'une projection du n-simplexe sur un plan, comme une ombre, les longueurs et les angles ne sont pas respectés : il faut s'imaginer que tous les segments sont de même longueur, et que tous les triangles qui relient 3 sommets sont équilatéraux si le simplexe est régulier. De plus, les diagonales du graphe ne se rencontrent jamais en réalité, mais passent devant ou derrière les autres.
Un graphe comme ceux-ci est aussi appelé polygone de Petrie car il est obtenu par la projection orthogonale d'un polytope sur un plan.
Diagramme de Coxeter-Dynkin
Le diagramme de Coxeter-Dynkin d'un n-simplexe est sous la forme : 






 …
…

 , avec n ronds (appelés nœuds) dans la chaîne.
, avec n ronds (appelés nœuds) dans la chaîne.
Symbole de Schläfli
Le symbole de Schläfli d'un n-simplexe est {3,3,3,..., 3,3}, avec n – 1 fois le nombre 3.
Propriétés
- Tout k-simplexe généré par un sous-ensemble de {a0, a1, … , an} (qui sont les sommets du simplexe s) est appelé k-face de s.
- L'ensemble des faces de s différentes de s lui-même sont appelées faces propres de s, et leur union est appelée bord de s.
- Un n-simplexe n'a pas de diagonales car par définition, les n + 1 sommets d'un n-simplexe sont déjà reliés entre eux.
- L'isobarycentre d'un n-simplexe est situé à des centres de ses (n – 1)-faces. Par exemple l'isobarycentre d'un segment est situé à 1/2 de ses extrémités, l'isobarycentre d'un triangle équilatéral est situé à 1/3 des milieux de ses côtés, l'isobarycentre d'un tétraèdre se situe à 1/4 des centres des faces...
- Un simplexe est son propre dual, ce qui signifie que lorsque l'on relie entre eux tous les centres des (n – 1)-faces d'un n-simplexe, on retombe sur le même simplexe, réduit d'un demi.
- Si un simplexe possède un « coin droit » (c'est-à-dire que toutes les arêtes se rencontrant en un sommet sont perpendiculaires en elles), on peut alors utiliser la généralisation en n dimensions du théorème de Pythagore : « La somme des carrés des (n –1)-volumes des hyperfaces adjacentes au coin droit est égale au carré du (n –1)-volume opposé au coin droit ». Par exemple, dans un triangle ABC rectangle en A on a , dans une pyramide ABCD rectangle en A on a , et dans un pentatope ABCDE rectangle en A on a .
- Topologiquement, un n-simplexe est homéomorphe à une n-sphère. Chaque n-simplexe est une variété convexe sans trous de dimension n. La caractéristique d'Euler de n'importe quel n-simplexe vaut donc 0 si n est pair et 2 si n est impair, comme pour la n-sphère.
- Le groupe des isométries du n-simplexe régulier est le groupe symétrique Sn+1.
Longueurs remarquables et volume du n-simplexe régulier
- La hauteur du n-simplexe régulier d'arête a est :
- ;
- le rayon de l'hypersphère circonscrite est :
- ;
- le rayon de l'hypersphère inscrite est :
- .
- .
-
- car la hauteur est perpendiculaire à toute droite de la (n – 1)-base, donc également au rayon de la (n – 1)-sphère circonscrite de la (n – 1)-base, et l'arête de longueur a relie le sommet de la hauteur avec un sommet de la base, les trois forment un triangle rectangle, on applique tout simplement le théorème de Pythagore.
-
- car le rayon de la n-sphère circonscrite relie le centre du n-simplexe à un sommet, le rayon de la sphère inscrite relie le centre du n-simplexe au centre de la base (comme la n-sphère inscrite est tangente au n-simplexe ce rayon est perpendiculaire à la base), et le rayon de la (n – 1)-sphère circonscrite à la base relie le centre de la base un sommet du n-simplexe, on applique encore le théorème de Pythagore.
Par récurrence, à partir de , on obtient les formules annoncées.
Chaque simplexe possède un hypervolume qui correspond à son intérieur (pour le segment il s'agit de sa longueur, pour le triangle de son aire, pour le tétraèdre de son volume). Le n-volume d'un n-simplexe est le produit d'une hauteur (distance entre un sommet et le centre de la (n – 1)-face opposée) et de la base correspondante ((n – 1)-volume de cette (n – 1)-face), divisé par la dimension du simplexe.
Si l'on note Vn le n-volume du n-simplexe régulier d'arête a, on a donc :
- .
Par récurrence, à partir de la longueur d'un segment () et de l'expression ci-dessus pour , on en déduit :
- .
- l'aire du triangle équilatéral est : ;
- le volume du tétraèdre régulier est : ;
- l'hypervolume du pentachore régulier est : .
Annexes
Articles connexes
- On parle aussi de simplexe pour désigner un algorithme permettant de résoudre les problèmes de programmation linéaire. Cet algorithme a été proposé par George Dantzig (voir Algorithme du simplexe).
- Autres n-polytopes réguliers : Solide de Platon, Solide d'Archimède, Polygone
- En théorie des graphes : voir Dimension (théorie des graphes)
- Grands mathématiciens qui ont étudié les polytopes : Euler, Poincaré, Coxeter, Schläfli, Riemann (qui, en premier, en 1854, a présenté le concept de variété et d'espace de dimension n)
- Simplexité
- L'hypervolume d'un simplexe quelconque en fonction des longueurs de arêtes est donné par le déterminant de Cayley-Menger.
Liens externes
- « Simplexe ou hypertétraèdre », sur Mathcurve
- (en) Eric W. Weisstein, « Simplex », sur MathWorld
Bibliographie
(en) James Munkres, Elements of Algebraic Topology (lire en ligne)
v · m | |||||
|---|---|---|---|---|---|
| Dimension 1 |
| ||||
| Dimension 2 |
| ||||
| Dimension 3 |
| ||||
| Dimension 4 |
| ||||
| Dimension ≥ 5 |
| ||||
 Portail de la géométrie
Portail de la géométrie





































