Truncated pentahexagonal tiling

Truncated pentahexagonal tiling
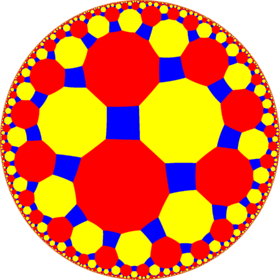Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.10.12
Schläfli symbol	tr{6,5} or ${\displaystyle t{\begin{Bmatrix}6\\5\end{Bmatrix}}}$
Wythoff symbol	2 6 5 |
Coxeter diagram
Symmetry group	[6,5], (*652)
Dual	Order 5-6 kisrhombille
Properties	Vertex-transitive

In geometry, the truncated tetrahexagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one decagon, and one dodecagon on each vertex. It has Schläfli symbol of t_0,1,2{6,5}. Its name is somewhat misleading: literal geometric truncation of pentahexagonal tiling produces rectangles instead of squares.

Dual tiling

The dual tiling is called an order-5-6 kisrhombille tiling, made as a complete bisection of the order-5 hexagonal tiling, here with triangles shown in alternating colors. This tiling represents the fundamental triangular domains of [6,5] (*652) symmetry.

Symmetry

There are four small index subgroup from [6,5] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

Small index subgroups of [6,5], (*652)

Index	1	2		6
Diagram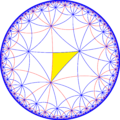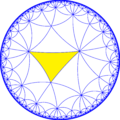
Coxeter (orbifold)	[6,5] = (*652)	[1+,6,5] = = (*553)	[6,5+] = (5*3)	[6,5*] = (*33333)
Direct subgroups
Index	2	4		12
Diagram
Coxeter (orbifold)	[6,5]+ = (652)	[6,5+]+ = = (553)		[6,5*]+ = (33333)

Related polyhedra and tilings

From a Wythoff construction there are fourteen hyperbolic uniform tilings that can be based from the regular order-5 hexagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 7 forms with full [6,5] symmetry, and 3 with subsymmetry.

Uniform hexagonal/pentagonal tilings v t e
Symmetry: [6,5], (*652)							[6,5]+, (652)	[6,5+], (5*3)	[1+,6,5], (*553)
{6,5}	t{6,5}	r{6,5}	2t{6,5}=t{5,6}	2r{6,5}={5,6}	rr{6,5}	tr{6,5}	sr{6,5}	s{5,6}	h{6,5}
Uniform duals
V65	V5.12.12	V5.6.5.6	V6.10.10	V56	V4.5.4.6	V4.10.12	V3.3.5.3.6	V3.3.3.5.3.5	V(3.5)5

See also

• Tilings of regular polygons
• List of uniform planar tilings

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch