射影加群

数学において、射影加群(しゃえいかぐん、英: projective module）とは、表現可能関手 Hom(P, –) が完全となるような加群 P のことである。自由加群の一般化に相当する。ホモロジー代数学における基本的な概念のひとつであり、Cartan & Eilenberg (1956)で導入された^[1]。

動機

一般の加群 P に対して表現可能関手 Hom(P, –) は左完全である。つまり任意の短完全列

0\to N\to M\to K\to 0

に対して

0\to \operatorname {Hom} (P,N)\to \operatorname {Hom} (P,M)\to \operatorname {Hom} (P,K)

は完全である。この関手 Hom(P, –) が完全となる、つまり

0\to \operatorname {Hom} (P,N)\to \operatorname {Hom} (P,M)\to \operatorname {Hom} (P,K)\to 0

が完全となる加群 P のことを射影加群と呼ぶ。

定義

R を単位元をもつ環とし、以下では加群はすべて左 R 加群、射はすべて左 R 加群の準同型を指すことにする。加群 P が射影加群である、あるいは射影的とは次の同値な条件のいずれかが成り立つことをいう^[2]。

関手 Hom(P, –) が完全である、つまり任意の短完全列 0 → N → M → K → 0 に対して 0 → Hom(P, N) → Hom(P, M) → Hom(P, K) → 0 も短完全列である
P はある自由加群の直和因子と同型である
任意の全射 N → M に対して Hom(P, N) → Hom(P, M) も全射である
任意の加群 M に対して Ext(P, M) = 0
任意の加群 M と正の整数 n に対して Extⁿ(P, M) = 0
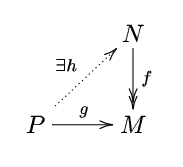
任意の全射 f : N → M と射 g : P → M に対して f・ h = g となる射 h : P → N が存在する

より一般にアーベル圏 ${\mathcal {A}}$ の対象 P は関手 $\operatorname {Hom} _{\mathcal {A}}(P,-)$ が完全なときに、射影的という。

例

環 R_i の直和 R = R₁ ⊕ R₂ に対して、P_i = R_i ⊕ 0 は射影的な R 加群であるが、自由加群ではない^[3]。

性質

環 R は半単純 ⇔ すべての左 R 加群は射影的^[4]
P_iはすべて射影加群 ⇔ ⊕P_i は射影加群^[5]
可換局所環上の有限生成射影加群は自由加群^[6]
体係数多項式環上の有限生成射影加群は自由加群（en:Quillen-Suslin theorem）

射影分解と射影次元

加群 M に対し、各 P_i が射影加群であるような次の完全列

\cdots \to P_{n+1}{\overset {d_{n+1}}{\to }}P_{n}\to \cdots \to P_{1}{\overset {d_{1}}{\to }}P_{0}{\overset {d_{0}}{\to }}M\to 0

を M の射影分解という^[7]。特にすべての i ≥ 0 に対して P_i → Im d_i が射影被覆となるときは極小射影分解という。任意の加群には自由分解（上記で射影加群を自由加群に置き換えたもの）が存在し、したがって射影分解も存在する。すべての i > n に対し P_i = 0 であるような射影分解を長さ n の射影分解という。そのような n が存在する場合その最小値を M の射影次元といい、存在しない場合は射影次元は ∞ という。ただし、{0} の射影次元は −1 とする。射影次元は pd(M) と書かれる。これは M の極小射影分解の長さに等しい。R-加群 M と整数 n ≥ 0 に対して以下は同値^[8]。

pd(M) ≤ n.
任意の R-加群 X に対して、 $\operatorname {Ext} _{R}^{n+1}(M,X)=\{0\}.$
任意の i ≥ n + 1 と任意の R-加群 X に対して、 $\operatorname {Ext} _{R}^{i}(M,X)=\{0\}.$

脚注

^ Weibel 1999, p. 816.
^ Anderson & Fuller 1992 17.1. Proposition(p.192), 17.2. Proposition(p.192), 岩永 & 佐藤 2002 補題 6-2-1(p.201)
^ Weibel 1994, Example 2.2.2.
^ Anderson & Fuller 1992, p. 193.
^ 岩永 & 佐藤 2002, p. 128.
^ Weibel 1994, Proposition 4.3.1.
^ Weibel 1994, Definition 2.2.4.
^ Weibel 1994, Lemma 4.1.6.

参考文献

Anderson, Frank W.; Fuller, Kent R. (1992). Rings and Categories of Modules. Graduate texts in mathematics. 13 (Second ed.). Springer-Verlag. ISBN 0-387-97845-3. MR1245487. Zbl 0765.16001. http://www.springer.com/mathematics/algebra/book/978-0-387-97845-1
Cartan, H.; Eilenberg, S. (1956). Homological Algebra. Princeton University Press. ISBN 0-444-82375-1. MR0077480. Zbl 0075.24305. https://books.google.co.jp/books?id=Sd0DDAAAQBAJ (Review by S. MacLane)
Weibel, Charles A. (1994). An Introduction to Homological Algebra. Cambridge University Press. ISBN 0-521-55987-1. MR1269324. Zbl 0797.18001. https://books.google.co.jp/books?id=flm-dBXfZ_gC&pg=PA33
Weibel, Charles A. (1999), “History of homological algebra”, in James, I. M., History of Topology, pp. 797–836, doi:10.1016/B978-044482375-5/50029-8, MR1721123, Zbl 0966.55002, https://books.google.co.jp/books?id=7iRijkz0rrUC&pg=PA797
岩永, 恭雄、佐藤, 眞久『環と加群のホモロジー代数的理論』（第1版）日本評論社、2002年。ISBN 4-535-78367-5。http://www.nippyo.co.jp/book/1984.html。数学 sugaku1947.58.413