Figurális számok
A figurális számok (ábrás számok, idomszámok) felfedezését a püthagoreusoknak tulajdonítják, akik a számokat kavicsokkal, magokkal szemléltették. Megpróbáltak különböző számú kavicsból szabályos alakzatokat kirakni. Azokat a számokat, amelyekből sikerült egy adott alakzat kirakása, figurális számoknak nevezték.[1] A figurális számok leggyakoribb használatuk szerint a háromszögszámok általánosítása különböző formákra (pl. sokszögszámok és középpontos sokszögszámok) és dimenziókra (poliéderszámok, politópszámok), de lehetnek L-alakok, csillag- vagy keresztformák stb.
Története
A figurális számok felfedezését a püthagoreusokhoz kötik, valószínűleg babiloni vagy egyiptomi előzményekkel. A gnómon használatát a figurális számok képzéséhez szintén Pitagorasznak tulajdonítják. Ezek az állítások nem nyugszanak biztos alapokon, mivel a püthagoreusokról szóló korabeli írásoknak[2] mind nyoma veszett, csak évszázadokkal későbbi információink vannak.[3] Az biztosnak látszik, hogy a negyedik, tíz kavicsból álló háromszögszám, a tetraktüsz a püthagoreusok vallásának központi eleme volt. A figurális számok fontosak voltak a pitagoraszi geometriában.
A figurális számok modern kori tanulmányozása Fermat-ig nyúl vissza, különösen a Fermat-féle sokszögszámtételig. Később fontos területét képezte Euler vizsgálódásainak, aki explicit képletet adott a háromszögű négyzetszámokra, más, figurális számokkal kapcsolatos felfedezései mellett.
A figurális számok fontos szerepet töltenek be a modern szórakoztató matematikában is.[4] Kutatások során Ehrhart-polinomokkal vizsgálják őket, amik egy sokszögben vagy poliéderben található egész koordinátájú pontok számát vizsgálják, ha adott faktorral bővítik őket.[5]
Háromszögszámok
A háromszögszámokat n = 1, 2, 3…-ra lineáris gnómonok egymásra helyezésével kaphatjuk meg:
 |    |       |           |                |                      |
Ezek az binomiális együtthatók. A háromszögszámok (r=2) más dimenziószámokra is érvényes általánosításai a szimplex politópszámok. Az r dimenziós szimplexek figurális számait a Pascal-háromszög r-edik átlója határozza meg.
A szimplex politópszámok r = 1, 2, 3, 4, …-re:
- (lineáris számok),
- (háromszögszámok),
- (tetraéderszámok),
- (pentatópszámok, 4-szimplex számok)
- (r-tóp számok, r-szimplex számok).
Sokszögszámok
Beszélhetünk középpontos és nem középpontos sokszögszámokról attól függően, hogy a kezdeti egyetlen pontot oldalirányban úgy egészítjük ki, hogy az eredeti pont a következő sokszög csúcsa legyen, vagy úgy, hogy a keletkező sokszög közepében helyezkedjen el.
(nem középpontos) Sokszögszámok
 | Bővebben: Sokszögszámok |
A sokszögszám olyan k szám, amihez létezik olyan szabályos sokszög, ami k számú, egymástól egyenlő távolságra lévő pontból kirakható. Például a 16 négyzetszám, mert 16 pontból ki lehet rakni egy négyzetet.
-
 A 10 háromszögszám.
A 10 háromszögszám. -
 A 16 négyzetszám.
A 16 négyzetszám. -
 A 22 ötszögszám.
A 22 ötszögszám. -
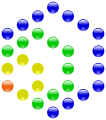 A 28 hatszögszám.
A 28 hatszögszám.
Középpontos sokszögszámok
 | Bővebben: Középpontos sokszögszámok |
A középpontos sokszögszámoknál a középpontban egy pont van, és azt sokszög alakú pontrétegek veszik körül. Adott réteg minden oldala eggyel több pontot tartalmaz, mint a korábbi réteg, így a második sokszögrétegtől kezdve egy középpontos k-szögszám minden rétege k-val több pontot tartalmaz a korábbinál:
-
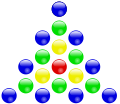 A 19 a negyedik középpontos háromszögszám.
A 19 a negyedik középpontos háromszögszám. -
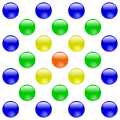 A 25 a negyedik középpontos négyzetszám.
A 25 a negyedik középpontos négyzetszám. -
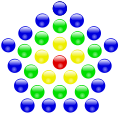 A 31 a negyedik középpontos ötszögszám.
A 31 a negyedik középpontos ötszögszám. -
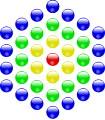 A 37 a negyedik középpontos hatszögszám.
A 37 a negyedik középpontos hatszögszám.
Fordítás
- Ez a szócikk részben vagy egészben a Figurate number című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
- Ez a szócikk részben vagy egészben a Figurierte Zahl című német Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.
Jegyzetek
- ↑ Tuzson Zoltán: A figurális számokról (I.) és Tuzson Zoltán: A figurális számokról (II.)
- ↑ Taylor, Thomas, The Theoretic Arithmetic of the Pythagoreans
- ↑ Boyer, Carl B. & Merzbach, Uta C., A History of Mathematics (Second ed.), p. 48
- ↑ Kraitchik, Maurice (2006), Mathematical Recreations (Second Revised ed.), Dover Books, ISBN 978-0-486-45358-3
- ↑ Beck, M.; De Loera, J. A. & Develin, M. et al. (2005), "Coefficients and roots of Ehrhart polynomials", Integer points in polyhedra—geometry, number theory, algebra, optimization, vol. 374, Contemp. Math., Providence, RI: Amer. Math. Soc., pp. 15–36.
- Gazalé, Midhat J. (1999), Gnomon: From Pharaohs to Fractals, Princeton University Press, ISBN 978-0-691-00514-0
- Deza, Elena & Michel Marie Deza (2012), Figurate Numbers, First Edition, World Scientific, ISBN 978-981-4355-48-3
- Heath, Thomas Little (2000), A history of Greek Mathematics: Volume 1. From Thales to Euclid, Adamant Media Corporation, ISBN 978-0-543-97448-8
- Heath, Thomas Little (2000), A history of Greek Mathematics: Volume 2. From Aristarchus to Diophantus, Adamant Media Corporation, ISBN 978-0-543-96877-7
- Dickson, Leonard Eugene (1923), History of the Theory of Numbers (three volume set), Chelsea Publishing Company, Inc.
- Boyer, Carl B. & Uta C. Merzbach, A History of Mathematics, Second Edition
További információk
- Figurális számok osztályozása
Kapcsolódó szócikkek
- Gnómon






















