Problème de l'obstacle

Le problème de l'obstacle est un exemple classique de motivation de l'étude mathématique des inégalités variationnelles et des problèmes à frontière libre. Il consiste à trouver la position d'équilibre d'une membrane élastique dont les bords sont fixes et devant passer au-dessus d'un obstacle donné. Il est profondément lié à l'étude des surfaces minimales et de la capacité d'un ensemble en théorie du potentiel. Les applications s'étendent à l'étude de la filtration d'un fluide en milieu poreux, au chauffage contraint, l'élastoplasticité, le contrôle optimal et les mathématiques financières^[1].

Mathématiquement, le problème se voit comme la minimisation de l'énergie de Dirichlet,

${\displaystyle J=\int _{D}|\nabla u|^{2}\mathrm {d} x}$

sur un domaine D où les fonctions u décrivent le déplacement vertical de la membrane. Les solutions doivent satisfaire des conditions au bord de Dirichlet et être supérieures à une fonction obstacle χ(x). La solution se distingue sur deux parties : une où elle est égale à l'obstacle (ensemble de contact) et une où elle y est strictement supérieure. L'interface entre les régions est appelée frontière libre.

En général, la solution est continue et sa dérivée est lipschitzienne, mais sa dérivée seconde est généralement discontinue à la frontière libre. La frontière libre est caractérisée comme une surface continue au sens de Hölder sauf en des points singuliers, situés sur une variété lisse.

Note historique

« Qualche tempo dopo Stampacchia, partendo sempre dalla sua disequazione variazionale, aperse un nuovo campo di ricerche che si rivelò importante e fecondo. Si tratta di quello che oggi è chiamato il problema dell'ostacolo. »

— Sandro Faedo, (Faedo 1986, p. 107)

ce qui peut se traduire en :

« Quelque temps après Stampacchia, en repartant de son inégalité variationnelle, est apparu un nouveau champ de recherches, qui s'est montré tout aussi important et riche. Il est maintenant appelé problème de l'obstacle [sic]. »

Approches intuitives

Forme d'une membrane sur un obstacle

Le problème de l'obstacle apparait quand on considère la forme prise par un film de savon dans un domaine dont la valeur à la frontière est fixée (comme le problème de Plateau), avec la contrainte ajoutée que la membrane doit passer au-dessus d'un obstacle χ(x) à l'intérieur du domaine^[2]. De plus, pour de petites variations, minimiser sa longueur revient à minimiser son énergie, en effet paramétrant l'élastique sur l'intervalle [-1,1] par

${\displaystyle \forall t\in [-1,1],\,{\begin{cases}x(t)=t\\y(t)=u(t).\end{cases}}}$

la longueur de l'élastique entre -1 et 1 est donnée par :

${\displaystyle l=\int _{-1}^{1}{\sqrt {1+u'(t)^{2}}}\mathrm {d} t}$.

L'objectif est donc de minimiser cette longueur, c'est-à-dire trouver

${\displaystyle \min _{u\in K}\int _{-1}^{1}{\sqrt {1+u'(t)^{2}}}\mathrm {d} t}$.

Or, si u' est suffisamment petit, le problème peut être linéarisé en remarquant que

${\displaystyle {\sqrt {1+u'(t)^{2}}}\sim 1+{\tfrac {1}{2}}u'(t)^{2}}$.

Minimiser la longueur de l'élastique revient donc à minimiser son énergie de Dirichlet :

${\displaystyle \min _{u\in K}\int _{-1}^{1}u'(t)^{2}\,\mathrm {d} t.}$

Arrêt optimal

En théorie du contrôle, le problème de l'obstacle peut venir en cherchant le temps d'arrêt optimal d'un processus stochastique avec une fonction de gain χ(x).

Dans le cas simple du mouvement brownien, et le processus doit s'arrêter dès qu'on sort du domaine, la solution u(x) du problème d'obstacle peut être caractérisée par la valeur attendue du succès, en commençant le process au point x, si la stratégie d'arrêt optimal est suivie. Le critère d'arrêt consiste à s'arrêter une fois l'ensemble de contact atteint^[3].

Formulation

On suppose :

1. un domaine ouvert borné D ⊂ ℝⁿ à frontière lisse
2. une fonction lisse f(x) sur ∂D (la frontière du domaine)
3. une fonction lisse χ(x) définie sur tout D telle que ${\displaystyle \chi |_{\partial D}<f}$, i.e. la restriction de χ sur la frontière de D (sa trace) est majorée par une fonction f.

Soit l'ensemble :

${\displaystyle K=\left\{u(x)\in H^{1}(D):u|_{\partial D}=f(x){\text{ et }}u\geq \chi \right\},}$

qui est un sous-ensemble fermé convexe de l'espace de Sobolev des fonctions de carré intégrable sur D et de dérivées faibles de carré intégrable, satisfaisant aux conditions voulues par rapport à l'obstacle. La solution au problème de l'obstacle est la fonction vérifiant :

${\displaystyle u=\operatorname {arg} \min _{v\in K}\int _{D}|\nabla v|^{2}\mathrm {d} x.}$

L'existence d'une solution est assurée par des considérations dans la théorie des espaces de Hilbert^[2],[4].

Formulations alternatives

Inégalités variationnelles

Le problème de l'obstacle peut être reformulé comme un problème standard dans le cadre des inégalités variationnelles sur les espaces de Hilbert. Chercher le minimisateur d'énergie dans l'ensemble K des fonctions admissibles est équivalent à chercher

${\displaystyle u\in K{\text{ tel que }}\forall v\in K,\int _{D}\langle {\nabla u},{\nabla (v-u)}\rangle \mathrm {d} x\geq 0}$

avec ⟨ . , . ⟩ : ℝⁿ × ℝⁿ → ℝ le produit scalaire classique sur ℝⁿ. C'est un cas particulier de la forme plus générale des inégalités variationnelles sur les espaces de Hilbert, de la forme

${\displaystyle a(u,v-u)\geq f(v-u)\qquad \forall v\in K.\,}$

avec K un sous-ensemble fermé convexe, a(u,v) une forme bilinéaire réelle bornée et coercive, f (v) une forme linaire bornée^[5].

Fonction surharmonique moindre

Un argument variationnel montre que hors de l'ensemble de contact, la solution du problème de l'obstacle est harmonique. Un argument similaire restreint aux variations positives montre qu'elle est surharmonique sur l'ensemble de contact. Ainsi, les deux arguments montre que la solution est surharmonique^[1].

En fait, par le principe du maximum, on voit que la solution au problème est la fonction la moins surharmonique dans l'ensemble des fonctions admissibles^[5].

Recherche intuitive de la solution

Etablissons un raisonnement afin de trouver une solution explicite au problème de l'obstacle où ${\displaystyle \chi (t)=1-2t^{2}}$ et ${\displaystyle g=0}$. L'obstacle est donc une parabole symétrique.

Forme de la solution près des bords

Comparaison d'énergies

La solution semble donc être (voir Fig. 3)

${\displaystyle u(t)={\begin{cases}T_{0}(t)\ &t\in [-1,t_{0}],\\\chi (t)\ &t\in [t_{0},t_{1}],\\T_{1}(t)\ &t\in [t_{1},1].\end{cases}}}$,

et on vérifie facilement que c'est le cas car cette solution vérifie le théorème de Stampacchia qui garantit son unicité :

${\displaystyle {\int _{-1}^{1}u'(v-u)'}=4{\int _{t_{0}}^{t_{1}}(v-\chi )}\geq 0.}$

Régularité

Régularité optimale

La solution à la dérivée de l’obstacle a une régularité de classe C^1,1, ou de dérivée seconde bornée, si l'obstacle a de telles propriétés^[6]. Plus précisément, les modules de continuité de la solution et de sa dérivée sont liés à ceux de l'obstacle.

1. si l'obstacle χ(x) a un module de continuité σ(r), donc tel que ${\displaystyle |\chi (x)-\chi (y)|\leq \sigma (|x-y|)}$, alors le module de continuité de la solution u(x) vaut C₀ σ(2r), avec C₀ une constante ne dépendant que du domaine (et pas de l'obstacle).
2. si la dérivée de l'obstacle a un module de continuité σ(r), alors la dérivée de la solution a pour module de continuité C₁ r σ(2r), avec C₁ une constante ne dépendant là aussi que du domaine^[7].

Surfaces de niveau et frontière libre

Sous une condition de dégénérescence, les niveaux de la différence entre la solution et l'obstacle ${\displaystyle \{x:u(x)-\chi (x)=t\}}$ pour t > 0 sont des surfaces C^1,α. La frontière libre, soit le bord du domaine de contact, est également C^1,α sauf sur un ensemble de points singuliers, eux-mêmes isolés ou localement contenus dans une variété de classe C^1[8].

Extensions du problème

Obstacle non concave

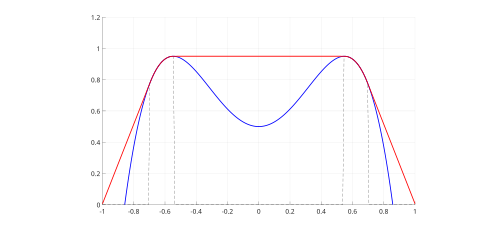
Considérons maintenant un autre obstacle, à savoir : ${\displaystyle \chi (t)=-5t^{4}+3t^{2}+0,5}$ sur ${\displaystyle I=[-1,1]}$. Le raisonnemement établi lors de l'étude de l'obstacle précédent nous laisse penser que la solution éventuelle serait de la forme (voir Fig. 4):

${\displaystyle u(t)=\left\{{\begin{array}{ll}a(t+1)&t\in [-1,t_{0}]\\\chi (t)&t\in [t_{0},t_{1}]\\\chi (t_{1})=\chi (t_{2})&t\in [t_{1},t_{2}]\\\chi (t)&t\in [t_{2},t_{3}]\\-a(t-1)&t\in [t_{3},1]\end{array}}\right.}$

où ${\displaystyle a\in \mathbb {R} }$ et ${\displaystyle t_{0},t_{1},t_{2},t_{3}}$ sont tels que :

• ${\displaystyle a(t+1)}$ est la tangente de ${\displaystyle \chi }$ au point d'abscisse ${\displaystyle t_{0}}$ s'annulant en ${\displaystyle -1}$ ,
• ${\displaystyle \chi (t)}$ atteint son maximum sur ${\displaystyle [-1,0]}$ au point ${\displaystyle t_{1}}$;
• Par symétrie, comme ${\displaystyle \chi }$ est une fonction paire, ${\displaystyle t_{1}=-t_{2}}$ et ${\displaystyle t_{3}=-t_{0}}$. Ainsi, ${\displaystyle \chi (t)}$ atteint son maximum sur ${\displaystyle [0,1]}$ au point ${\displaystyle t_{2}}$ et ${\displaystyle -a(t-1)}$ est la tangente de ${\displaystyle \chi }$ au point d'abscisse ${\displaystyle t_{3}}$ s'annulant en ${\displaystyle 1}$.

Cette solution vérifie bien le théorème de Stampacchia car

${\displaystyle {\int _{-1}^{1}u'(v-u)'}={\int _{t_{0}}^{t_{1}}\chi ''(\chi -v)}+{\int _{t_{2}}^{t_{3}}\chi ''(\chi -v)}\geq 0}$

et est donc l'unique solution.

Double obstacle

En considérant maintenant le convexe fermé

${\displaystyle K'=\left\{u\in H_{0}^{1}(-1,1){\text{ tel que }}\chi ^{-}\leq u\leq \chi ^{+}{\text{ presque partout }}\right\}}$,

on peut alors étudier le problème à deux obstacles. Considérons les obstacles ${\displaystyle \chi ^{-}(t)=-5t^{4}+3t^{2}+0,5}$ et ${\displaystyle \chi ^{+}(t)=4t^{2}+0,7}$ sur ${\displaystyle I=[-1,1]}$.

Le raisonnemement établi précédemment laisse penser que la solution éventuelle serait de la forme (voir Fig. 5):

${\displaystyle u(t)={\begin{cases}at+a\,&t\in [-1,t_{0}]\\\chi ^{-}(t)\ &t\in [t_{0},t_{1}]\\bt+c\,&t\in [t_{1},t_{2}]\\\chi ^{+}(t)\ &t\in [t_{2},t_{3}]\\-bt+c\,&t\in [t_{3},t_{4}]\\\chi ^{-}(t)\ &t\in [t_{4},t_{5}]\\-at+a\,&t\in [t_{5},1]\end{cases}}}$

où ${\displaystyle a,b,c\in \mathbb {R} }$ et ${\displaystyle t_{0},t_{1},t_{2},t_{3},t_{4}}$ et ${\displaystyle t_{5}}$ sont tels que

• ${\displaystyle at+a}$ est la tangente de ${\displaystyle \chi ^{-}}$ au point d'abscisse ${\displaystyle t_{0}}$ s'annulant en ${\displaystyle -1}$,
• ${\displaystyle bt+c}$ est la tangente commune aux deux obstacles. Elle est la tangente de ${\displaystyle \chi ^{-}}$ au point d'abscisse ${\displaystyle t_{1}}$ et est la tangente de ${\displaystyle \chi ^{+}}$ au point d'abscisse ${\displaystyle t_{2}}$.
• Par symétrie, comme ${\displaystyle \chi ^{-}}$ et ${\displaystyle \chi ^{+}}$ sont deux fonctions paires, ${\displaystyle t_{0}=-t_{5}}$, ${\displaystyle t_{1}=-t_{4}}$ et ${\displaystyle t_{2}=-t_{3}}$. Ainsi, ${\displaystyle -bt+c}$ est la tangente de ${\displaystyle \chi ^{+}}$ au point d'abscisse ${\displaystyle t_{3}}$ et est la tangente de ${\displaystyle \chi ^{-}}$ au point d'abscisse ${\displaystyle t_{4}}$ et

${\displaystyle -at+a}$ est la tangente de ${\displaystyle \chi ^{-}}$ au point d'abscisse ${\displaystyle t_{5}}$ s'annulant en ${\displaystyle 1}$.

Par les mêmes calculs que précédemment, il est facile de voir que cette solution vérifie le théorème de Stampacchia et est donc l'unique solution.

Problème en dimensions supérieures à 2

Le problème de l'obstacle peut être étudié en dimension supérieure, en utilisant alors la notion de gradient à la place des dérivées. Une des applications physiques est le recouvrement d'un objet par une membrane élastique.

En effet, sur un ouvert borné ${\displaystyle \Omega }$ de ${\displaystyle \mathbb {R} ^{n}}$, pour ${\displaystyle u\in H_{0}^{1}(\Omega )}$, nous avons l'expression de la mesure de la surface de ${\displaystyle u}$ suivante :

${\displaystyle l(u)=\int _{\Omega }{\sqrt {1+\|\nabla u\|^{2}}}\mathrm {d} x}$

Cette quantité est bien définie sur ${\displaystyle H_{0}^{1}(\Omega )}$, car sachant que ${\displaystyle \forall x\in \mathbb {R} ^{+}}$, on a ${\displaystyle {\sqrt {1+x}}\leq 1+{\frac {1}{2}}x}$, alors on obtient l'inégalité :

${\displaystyle \int _{\Omega }{\sqrt {1+\|\nabla u\|^{2}}}\mathrm {d} x\leq \int _{\Omega }\left(1+{\cfrac {1}{2}}\|\nabla u\|^{2}\right)\mathrm {d} x=|\Omega |+{\cfrac {1}{2}}\|\nabla u\|_{L^{2}}^{2}}$

De même qu'en dimension 1, il est possible de linéariser le problème, de façon analogue, ainsi le problème original dans lequel la nouvelle quantité à minimiser devient :

${\displaystyle J(u)={\cfrac {1}{2}}\int _{\Omega }\|\nabla u\|^{2}\mathrm {d} x}$

Autres généralisations

La théorie du problème de l'obstacle peut s'étendre aux opérateurs elliptiques^[5] et leurs fonctionnelles énergies associées, ou même les opérateurs elliptiques dégénérés.

Le problème de Signorini est une variante du problème de l’obstacle, où la fonctionnelle énergie est minimisée sous une contrainte définie sur une surface d'une dimension moindre, comme le problème de l'obstacle aux frontières, où la contrainte s'applique au bord du domaine.

Les cas dépendant du temps, ou parabolique, sont également des sujets d'étude.

Voir aussi

• Surface minimale
• Problème de Plateau
• Option barrière
• Inégalité variationnelle
• Problème de Signorini

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Obstacle problem » (voir la liste des auteurs).

Notes

• (it) Sandro Faedo, « Convegno celebrativo del centenario della nascita di Mauro Picone e Leonida Tonelli (6–9 maggio 1985) », Atti dei Convegni Lincei, Roma, Accademia Nazionale dei Lincei, vol. 77,‎ 1986, p. 89–109 (lire en ligne). "Leonida Tonelli et l'école mathématique de Pise" est une étude sur l'oeuvre de Tonelli à Pise et son influence dans le développement de l’école, présentée à l' International congress in occasion of the celebration of the centenary of birth of Mauro Picone and Leonida Tonelli (tenue à Rome entre le 6 et le 9 mai 1985). L'auteur était un de ses élèves et, après sa mort, a obtenu sa chaire d'analyse mathématique à l'Université de Pise, devenant doyen de la faculté des sciences puis recteur : il a exercé une forte influence positive sur le développement de l'université.
• (en) Luis Caffarelli, « The obstacle problem revisited », The Journal of Fourier Analysis and Applications, vol. 4, n^os 4–5,‎ juillet 1998, p. 383–402 (DOI 10.1007/BF02498216, MR 1658612, zbMATH 0928.49030, lire en ligne)
• (en) Lawrence C. Evans, « An Introduction to Stochastic Differential Equations », 1988 (consulté le 11 juillet 2011). Un ensemble de présentations « sans trop de détails précis, les bases de la théorie des probabilités, des équations différentielels aléatoires et quelques applications », selon les mots de l'auteur.
• (en) Jens Frehse, « On the regularity of the solution of a second order variational inequality », Bolletino della Unione Matematica Italiana, serie IV,, vol. 6,‎ 1972, p. 312–315 (MR 318650, zbMATH 0261.49021).
• (en) Avner Friedman, Variational principles and free boundary problems, New York, John Wiley & Sons, 1982, ix+710 (ISBN 0-471-86849-3, MR 0679313, zbMATH 0564.49002).
• (en) David Kinderlehrer et Guido Stampacchia, « An Introduction to Variational Inequalities and Their Applications », Pure and Applied Mathematics, New York, Academic Press, vol. 88,‎ 1980, xiv+313 (ISBN 0-12-407350-6, MR 0567696, zbMATH 0457.35001)
• (en) Luis Caffarelli, « The Obstacle Problem revisited », Journal of Fourier Analysis and Applications,‎ août 1998, p. 383-402 (lire en ligne)

• Portail de la physique
• Portail de l'analyse