Loi zêta


Cet article ne cite pas suffisamment ses sources ().
Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».
En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?
| Zêta | |
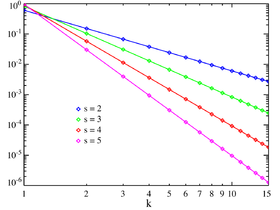 Fonction de masse | |
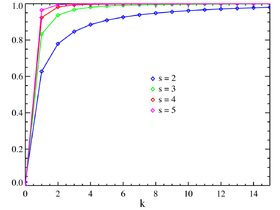 Fonction de répartition | |
modifier  |
En théorie de probabilité et statistiques, la distribution zêta est une loi de probabilité discrète de paramètre [1]. Elle est aussi appelée loi de Pareto discrète[2], en lien avec la loi de Pareto.
Définition
On dit qu'une variable aléatoire suit une loi zêta de paramètre si :
où est la fonction zêta de Riemann non définie en 1[1].
Une loi zêta est un sous cas de la loi de Zipf où le paramètre N est infini.
Moments
Le n-ième moment est défini par l'espérance de Xn :
La série de droite est une représentation de la fonction zêta de Riemann et converge seulement pour les valeurs de s-n strictement supérieures à 1. Ainsi :
Lien avec la densité naturelle
Soit A une partie de , on dit que A a une densité naturelle si converge. Notons d(A) la limite. On a alors le résultat suivant :
Soit , posons pour tout on a par hypothèse que , donc on peut poser tel que
On écrit alors
On s'intéresse au terme , on a : car la variable muette a est supérieure à
Sans nuire à la généralité, supposons A infini (le cas A fini est trivial), écrivons alors . Il s'ensuit alors que pour . posons alors
On a donc , d'où
On fait alors de même à gauche et on trouve pour s assez proche de 1 que , ainsi :
Voir aussi
- Loi de Cauchy
- Loi de Lévy
- Loi de Pareto
- Loi de Zipf
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Zeta distribution » (voir la liste des auteurs).
v · m Index du projet probabilités et statistiques | |||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||
 Portail des probabilités et de la statistique
Portail des probabilités et de la statistique






































