Poligono erregular
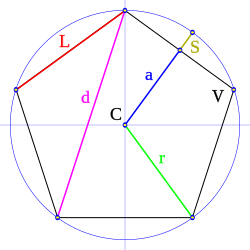
- C = zirkunferentzia zirkunskribatuaren zentroa
- V = poligonoaren erpin bat
- L = poligonoaren alde bat
- d = poligonoaren diagonal bat
- r = zirkunferentzia zirkunskribatuaren erradioa
- a = poligonoaren apotema
Geometrian, poligono bat erregularra da, aldeberdina (alde guztiak luzera berekoak dira) eta angeluberdina (angelu guztiak neurri berekoak dira) bada.
Poligono erregularrak bi motatakoak izan daitezke: ganbilak eta ahurrak (izar itxurakoak azken horiek, izar-poligono izenekoak).
Hiru eta lau aldeko poligono erregularrak triangelu aldeberdina eta karratua dira, hurrenez hurren; alde gehiagoko poligono erregularrak izendatzeko, erregular terminoa gehitzen da (pentagono erregularra, hexagono erregularra...).
Poligono erregularren elementuak
- Aldea (L): poligonoa osatzen duten zuzenkietako bakoitza
- Erpina (V): poligono baten bi aldek elkar ebakitzen duten puntua
- Zentroa (C): erpinetatik distantziakidea den puntua
- Erradioa (r): poligonoaren zentroa eta erpin bat lotzen dituen zuzenkia
- Apotema (a): aldearekiko elkarzuta den eta poligonoaren zentroraino doan zuzenkia
- Diagonala (d): ondoz ondokoak ez diren bi erpin lotzen dituen zuzenkia
- Perimetroa (P): alde guztien luzeren batura
Poligono erregularren propietateak
- n aldeko poligono erregularrak n ordenako biraketa-simetria du.
- Erpin guztiak zirkunferentzia berean daude (zirkunferentzia zirkunskribatua); hau da, erpinak ziklokideak dira. Beraz, poligono erregularrak ziklikoak dira.
- Aurreko bi propietateetatik, eta kontuan hartuta aldeak berdinak direla, ondoriozta daiteke poligono erregular guztiek zirkunferentzia inskribatu bat daukatela, alde guztien erdiguneak barnetik ukitzen dituena. Hortaz, poligono erregularrak poligono ukitzaileak dira.
- Poligono erregularretan, angelu zentralak eta kanpo-angeluak berdinak dira.
Poligono erregularren angeluak
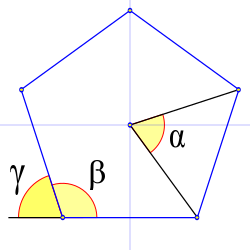
β = barne-angelua,
γ = kanpo-angelua
Angelu zentrala
- Poligono erregular baten angelu zentralak () kongruenteak dira, eta haien neurria honela kalkula daiteke, poligonoaren alde kopuruaren (n) arabera:
- (gradu hirurogeitarretan)
- (radianetan)
Barne-angelua
- Poligono erregular baten barne-angelua () honela kalkula daiteke:
- (gradu hirurogeitarretan)
- (radianetan)
- Poligono erregular baten barne-angeluen batura (), beraz:
- (gradu hirurogeitarretan)
- (radianetan)
Kanpo-angelua
- Poligono erregular baten kanpo-angelua () honela kalkula daiteke:
- (gradu hirurogeitarretan)
- (radianetan)
- Poligono erregular baten kanpo-angeluen batura (), beraz:
- (gradu hirurogeitarretan)
- (radianetan)
Poligono erregular batzuk
-
 Triangelu aldeberdina (triangelu erregularra) (3)
Triangelu aldeberdina (triangelu erregularra) (3) -

-
 Pentagono erregularra (5)
Pentagono erregularra (5) -
 Hexagono erregularra (6)
Hexagono erregularra (6) -
 Heptagono erregularra (7)
Heptagono erregularra (7) -
 Oktogono erregularra (8)
Oktogono erregularra (8) -
 Eneagono erregularra (9)
Eneagono erregularra (9) -
 Dekagono erregularra (10)
Dekagono erregularra (10) -
 Endekagono erregularra (11)
Endekagono erregularra (11) -
 Dodekagono erregularra (12)
Dodekagono erregularra (12) -
 Tridekagono erregularra (13)
Tridekagono erregularra (13) -
 Tetradekagono erregularra (14)
Tetradekagono erregularra (14)
Oharra: Poligono erregularrak zenbat eta alde gehiago izan, orduan eta zirkunferentzia baten antz handiagoa izango du.
Poligono erregularraren azalera
Poligono erregular baten azalera kalkulatzeko, ezagunak ditugun elementuen arabera, hainbat formula daude:
Azalera: perimetroaren eta apotemaren arabera
| Froga |

|
Azalera: alde kopuruaren eta apotemaren arabera
| Froga |

|
Azalera: alde kopuruaren eta erradioaren arabera
| Froga |

|
Azalera: aldearen arabera
| Froga |
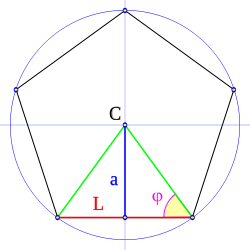
|
Laburpen-taula
Oharra: alde kopuru oso handia duen poligonoaren kasuan, barne-angeluek lauak izatera joko dute, aldea nulua izatera eta azalera π zenbakiaren baliorantz[1].
| Alde, angelu eta erpin kopurua | Poligonoa | Irudia | Barne-angelua | Aldea[1] | Azalera[1] | Animazioa: eraikitze grafikoa erregela eta konpasa erabiliz |
|---|---|---|---|---|---|---|
| 3 | Triangelu aldeberdina |  | 60° | √3≅1,732 | 3/4·√3≅1,299 | Eraikitze zehatza |
| 4 | Karratua |  | 90° | √2≅1,414 | 2 | Eraikitze zehatza |
| 5 | Pentagonoa |  | 108° | ≅1,176 | ≅2,378 | Eraikitze zehatza |
| 6 | Hexagonoa |  | 120° | 1 | 3/2·√3≅2598 | Eraikitze zehatza |
| 7 | Heptagonoa |  | ≅128,57° | ≅0,868 | ≅2,736 | Gutxi gorabeherako eraikitzea |
| 8 | Oktogonoa |  | 135° | ≅0,765 | 2·√2≅2,828 | Eraikitze zehatza |
| 9 | Eneagonoa |  | 140° | ≅0,684 | ≅2,893 | Gutxi gorabeherako eraikitzea |
| 10 | Dekagonoa |  | 144° | ≅0,618 | ≅2,939 | Eraikitze zehatza |
| 11 | Endekagonoa |  | ≅147,27° | ≅0,563 | ≅2,974 | Gutxi gorabeherako eraikitzea |
| 12 | Dodekagonoa |  | 150° | ≅0,518 | 3 | Eraikitze zehatza |
| 13 | Tridekagonoa |  | ≅152,31° | ≅0,479 | ≅3,021 | Gutxi gorabeherako eraikitzea |
| 14 | Tetradekagonoa |  | ≅154,29° | ≅0,445 | ≅3,037 | Gutxi gorabeherako eraikitzea |
| 15 | Pentadekagonoa |  | 156° | ≅0,416 | ≅3,051 | Eraikitze zehatza |
| 16 | Hexadekagonoa |  | 157,5° | ≅0,390 | ≅3,061 | Eraikitze zehatza |
| 17 | Heptadekagonoa |  | ≅158,82° | ≅0,367 | ≅3,071 | Eraikitze zehatza 34-gonoa, 51-gonoa 85-gonoa, 255-gonoa |
| 18 | Oktodekagonoa |  | 160° | ≅0,347 | ≅3,078 | Gutxi gorabeherako eraikitzea |
| 19 | Eneadekagonoa |  | ≅161,05° | ≅0,329 | ≅3,085 | Gutxi gorabeherako eraikitzea |
| 20 | Ikosagonoa |  | 162° | ≅0,313 | ≅3,090 | Eraikitze zehatza |
| 257 | 257-gonoa | ≅178,6° | ≅0,024 | ≅3,141 | Eraikitze zehatza | |
| 65.537 | 65.537-gonoa | ≅179,9945° | ≅0,000096 | ≅3,1416 | Eraikitze partziala |
Erreferentziak eta oharrak
- ↑ a b c Zirkunferentzia zirkunskribatuaren erradioak 1 balio duenean.
Kanpo estekak
 Datuak: Q714886
Datuak: Q714886 Multimedia: Regular polygons / Q714886
Multimedia: Regular polygons / Q714886































































