matemáticas , la sustitución trigonométrica consiste en la sustitución de determinadas expresiones mediante el uso de funciones trigonométricas . En cálculo , la sustitución trigonométrica es una técnica que permite evaluar integrales, puesto que se pueden utilizar identidades trigonométricas para simplificar ciertas integrales que contienen expresiones radicales .[ 1] [ 2]
Caso I: Integrando conteniendo a 2 − x 2 {\displaystyle a^{2}-x^{2}} Se hace el cambio de variable x = a sen θ {\displaystyle x=a\operatorname {sen} \theta } identidad trigonométrica sen 2 ( θ ) + cos 2 ( θ ) = 1 {\displaystyle \operatorname {sen} ^{2}(\theta )+\cos ^{2}(\theta )=1}
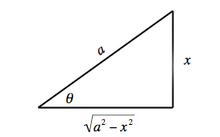
Construcción geométrica para Caso I {\displaystyle {\text{I}}} Integral Indefinida Ejemplo I Para calcular la integral
∫ d x a 2 − x 2 {\displaystyle \int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}} se puede realizar el cambio de variable
x = a sen θ d x = a cos θ d θ θ = arcsen ( x a ) {\displaystyle {\begin{aligned}x&=a\operatorname {sen} \theta \\dx&=a\cos \theta \;d\theta \\\theta &={\text{arcsen}}\left({\frac {x}{a}}\right)\end{aligned}}} entonces
∫ d x a 2 − x 2 = ∫ a cos θ a 2 − a 2 sen 2 θ d θ = ∫ a cos θ a 2 ( 1 − sen 2 θ ) d θ = ∫ a cos θ a 2 cos 2 θ d θ = ∫ d θ = θ + C = arcsen ( x a ) + C {\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta }{\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\;d\theta \\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&={\text{arcsen}}\left({\frac {x}{a}}\right)+C\end{aligned}}} Los pasos anteriores requirieron que a > 0 {\displaystyle a>0} cos θ > 0 {\displaystyle \cos \theta >0}
Es posible escoger a {\displaystyle a} a 2 {\displaystyle a^{2}} − π / 2 < θ < π / 2 {\displaystyle -\pi /2<\theta <\pi /2} arco seno .
Para una integral definida, se debe averiguar cómo cambian los límites de la integración. Por ejemplo, cuando x {\displaystyle x} 0 {\displaystyle 0} a / 2 {\displaystyle a/2} sen θ {\displaystyle \operatorname {sen} \theta } 0 {\displaystyle 0} 1 / 2 {\displaystyle 1/2} θ {\displaystyle \theta } 0 {\displaystyle 0} π / 6 {\displaystyle \pi /6}
∫ 0 a / 2 d x a 2 − x 2 = ∫ 0 π / 6 d θ = π 6 . {\displaystyle \int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}=\int _{0}^{\pi /6}d\theta ={\frac {\pi }{6}}.} Se necesita elegir los límites con cuidado. Debido a que la integración anterior requiere que − π / 2 < θ < π / 2 {\displaystyle -\pi /2<\theta <\pi /2} θ {\displaystyle \theta } 0 {\displaystyle 0} π / 6 {\displaystyle \pi /6} θ {\displaystyle \theta } π {\displaystyle \pi } 5 π / 6 {\displaystyle 5\pi /6}
Alternativamente, se deben evaluar completamente las integrales indefinidas antes de aplicar las condiciones de contorno. En ese caso, la antiderivada da
∫ 0 a / 2 d x a 2 − x 2 = arcsen ( x a ) | 0 a / 2 = arcsen ( 1 2 ) − arcsen ( 0 ) = π 6 {\displaystyle {\begin{aligned}\int _{0}^{a/2}{\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\operatorname {arcsen} \left({\frac {x}{a}}\right){\Biggl |}_{0}^{a/2}\\&=\operatorname {arcsen} \left({\frac {1}{2}}\right)-\operatorname {arcsen} (0)\\&={\frac {\pi }{6}}\end{aligned}}} como antes.
Ejemplo II La integral
∫ a 2 − x 2 d x {\displaystyle \int {\sqrt {a^{2}-x^{2}}}\,dx} puede ser evaluada haciendo el cambio de variable
x = a sen θ d x = a cos θ d θ θ = arcsen ( x a ) {\displaystyle {\begin{aligned}x&=a\operatorname {sen} \theta \\dx&=a\cos \theta \;d\theta \\\theta &={\text{arcsen}}\left({\frac {x}{a}}\right)\end{aligned}}} donde a > 0 {\displaystyle a>0} a 2 = a {\displaystyle {\sqrt {a^{2}}}=a}
− π 2 ≤ θ ≤ π 2 {\displaystyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}} porque cos θ ≥ 0 {\displaystyle \cos \theta \geq 0} cos 2 θ = cos θ {\displaystyle {\sqrt {\cos ^{2}\theta }}=\cos \theta }
Luego
∫ a 2 − x 2 d x = ∫ a 2 − a 2 sen 2 θ ( a cos θ ) d θ = ∫ a 2 ( 1 − sen 2 θ ) ( a cos θ ) d θ = ∫ a 2 ( cos 2 θ ) ( a cos θ ) d θ = ∫ ( a cos θ ) ( a cos θ ) d θ = a 2 ∫ cos 2 θ d θ = a 2 ∫ ( 1 + cos 2 θ 2 ) d θ = a 2 2 ( θ + 1 2 sen 2 θ ) + C = a 2 2 ( θ + sen θ cos θ ) + C = a 2 2 ( arcsen ( x a ) + x a 1 − x 2 a 2 ) + C = a 2 2 arcsen ( x a ) + x 2 a 2 − x 2 + C {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\operatorname {sen} \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left({\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\;{\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C\end{aligned}}} Integral Definida Para una integral definida, los límites de integración cambian una vez que se realiza la sustitución y estos están determinados por
θ = arcsen ( x a ) {\displaystyle \theta ={\text{arcsen}}\left({\frac {x}{a}}\right)} con valores para θ {\displaystyle \theta }
− π 2 ≤ θ ≤ π 2 {\displaystyle -{\frac {\pi }{2}}\leq \theta \leq {\frac {\pi }{2}}} Ejemplo I Considérese la integral definida
∫ − 1 1 4 − x 2 d x {\displaystyle \int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx} que puede ser evaluada haciendo el cambio de variable
x = 2 sen θ d x = 2 cos θ d θ {\displaystyle {\begin{aligned}x&=2\operatorname {sen} \theta \\dx&=2\cos \theta \,d\theta \end{aligned}}} y en este caso, los límites de integración estarán determinados por
θ = arcsen ( x 2 ) {\displaystyle \theta ={\text{arcsen}}\left({\frac {x}{2}}\right)} Tenemos que
si x = − 1 {\displaystyle x=-1} θ = arcsen ( − 1 2 ) = − π 6 {\displaystyle \theta ={\text{arcsen}}\left(-{\frac {1}{2}}\right)=-{\frac {\pi }{6}}}
y si x = 1 {\displaystyle x=1} θ = arcsen ( 1 2 ) = π 6 {\displaystyle \theta ={\text{arcsen}}\left({\frac {1}{2}}\right)={\frac {\pi }{6}}}
entonces
∫ − 1 1 4 − x 2 d x = ∫ − π / 6 π / 6 4 − 4 sen 2 θ ( 2 cos θ ) d θ = ∫ − π / 6 π / 6 4 ( 1 − sen 2 θ ) ( 2 cos θ ) d θ = ∫ − π / 6 π / 6 4 ( cos 2 θ ) ( 2 cos θ ) d θ = ∫ − π / 6 π / 6 ( 2 cos θ ) ( 2 cos θ ) d θ = 4 ∫ − π / 6 π / 6 cos 2 θ d θ = 4 ∫ − π / 6 π / 6 ( 1 + cos 2 θ 2 ) d θ = 2 [ θ + 1 2 sen 2 θ ] − π / 6 π / 6 = [ 2 θ + sen 2 θ ] | − π / 6 π / 6 = ( π 3 + sen π 3 ) − ( − π 3 + sen ( − π 3 ) ) = 2 π 3 + 3 {\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\operatorname {sen} ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\operatorname {sen} ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right]_{-\pi /6}^{\pi /6}\\[6pt]&=[2\theta +\operatorname {sen} 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\operatorname {sen} {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\operatorname {sen} \left(-{\frac {\pi }{3}}\right)\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}} Por otro lado, si aplicamos directamente los límites de integración para la fórmula de la antiderivada obtenemos
∫ − 1 1 4 − x 2 d x = [ 2 arcsen ( x 2 ) + x 2 4 − x 2 ] − 1 1 = ( 2 arcsen ( 1 2 ) + 1 2 3 ) − ( 2 arcsen ( − 1 2 ) − 1 2 3 ) = ( 2 ⋅ π 6 + 3 2 ) − ( 2 ⋅ ( − π 6 ) − 3 2 ) = 2 π 3 + 3 {\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[2\;{\text{arcsen}}\left({\frac {x}{2}}\right)+{\frac {x}{2}}{\sqrt {4-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\;{\text{arcsen}}\left({\frac {1}{2}}\right)+{\frac {1}{2}}{\sqrt {3}}\right)-\left(2\;{\text{arcsen}}\left(-{\frac {1}{2}}\right)-{\frac {1}{2}}{\sqrt {3}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}} Caso II: Integrando conteniendo a 2 + x 2 {\displaystyle a^{2}+x^{2}} Se hace el cambio de variable x = a tan θ {\displaystyle x=a\tan \theta } identidad trigonométrica sec 2 ( θ ) − tan 2 ( θ ) = 1 {\displaystyle \sec ^{2}(\theta )-\tan ^{2}(\theta )=1}
Integral Indefinida Construcción geométrica para Caso II {\displaystyle {\text{II}}} Ejemplo I En la integral
∫ d x a 2 + x 2 {\displaystyle \int {\frac {dx}{a^{2}+x^{2}}}} hacemos el cambio de variable
x = a tan θ d x = a sec 2 θ d θ θ = arctan ( x a ) {\displaystyle {\begin{aligned}x&=a\tan \theta \\dx&=a\sec ^{2}\theta \;d\theta \\\theta &=\arctan \left({\frac {x}{a}}\right)\end{aligned}}} de modo que la integral se convierte en
∫ d x a 2 + x 2 = ∫ a sec 2 θ a 2 + a 2 tan 2 θ d θ = ∫ a sec 2 θ a 2 ( 1 + tan 2 θ ) d θ = ∫ a sec 2 θ a 2 sec 2 θ d θ = 1 a ∫ d θ = θ a + C = 1 a arctan ( x a ) + C {\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\,d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}(1+\tan ^{2}\theta )}}\;d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}\sec ^{2}\theta }}\,d\theta \\[6pt]&={\frac {1}{a}}\int d\theta \\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C\end{aligned}}} para a ≠ 0 {\displaystyle a\neq 0}
Ejemplo II La integral
∫ a 2 + x 2 d x {\displaystyle \int {\sqrt {a^{2}+x^{2}}}\,{dx}} puede ser evaluada haciendo el cambio de variable
x = a tan θ d x = a sec 2 θ d θ θ = arctan ( x a ) {\displaystyle {\begin{aligned}x&=a\tan \theta \\dx&=a\sec ^{2}\theta \,d\theta \\\theta &=\arctan \left({\frac {x}{a}}\right)\end{aligned}}} donde a > 0 {\displaystyle a>0} a 2 = a {\displaystyle {\sqrt {a^{2}}}=a}
− π 2 < θ < π 2 {\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}} por lo que sec θ > 0 {\displaystyle \sec \theta >0} sec 2 θ = sec θ {\displaystyle {\sqrt {\sec ^{2}\theta }}=\sec \theta }
Entonces
∫ a 2 + x 2 d x = ∫ a 2 + a 2 tan 2 θ ( a sec 2 θ ) d θ = ∫ a 2 ( 1 + tan 2 θ ) ( a sec 2 θ ) d θ = ∫ a 2 sec 2 θ ( a sec 2 θ ) d θ = ∫ ( a sec θ ) ( a sec 2 θ ) d θ = a 2 ∫ sec 3 θ d θ . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}} La integral de la secante cúbica puede ser evaluada utilizando integración por partes , dando como resultado
∫ a 2 + x 2 d x = a 2 2 ( sec θ tan θ + ln | sec θ + tan θ | ) + C = a 2 2 ( 1 + x 2 a 2 ⋅ x a + ln | 1 + x 2 a 2 + x a | ) + C = 1 2 ( x a 2 + x 2 + a 2 ln | x + a 2 + x 2 | ) + C . {\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|x+{\sqrt {a^{2}+x^{2}}}\right|\right)+C.\end{aligned}}} Integral Definida Para una integral definida, los límites de integración cambian una vez que se hace la sustitución y estos están determinados por
θ = arctan ( x a ) {\displaystyle \theta =\arctan \left({\frac {x}{a}}\right)} con valores para θ {\displaystyle \theta }
− π 2 < θ < π 2 {\displaystyle -{\frac {\pi }{2}}<\theta <{\frac {\pi }{2}}} Ejemplo I Considérese la integral definida
∫ 0 1 4 1 + x 2 d x {\displaystyle \int _{0}^{1}{\frac {4}{1+x^{2}}}\,dx} esta puede ser evaluada haciendo el cambio de variable
x = tan θ d x = sec 2 θ d θ {\displaystyle {\begin{aligned}x&=\tan \theta \\dx&=\sec ^{2}\theta \,d\theta \end{aligned}}}
con los límites de integración determinados por θ = arctan x {\displaystyle \theta =\arctan x}
Tenemos que
si x = 0 {\displaystyle x=0} θ = arctan ( 0 ) = 0 {\displaystyle \theta =\arctan(0)=0}
y si x = 1 {\displaystyle x=1} θ = arctan ( 1 ) = π 4 {\displaystyle \theta =\arctan(1)={\frac {\pi }{4}}}
de modo que
∫ 0 1 4 1 + x 2 d x = 4 ∫ 0 π / 4 sec 2 θ 1 + tan 2 θ d θ = 4 ∫ 0 π / 4 sec 2 θ sec 2 θ d θ = 4 ∫ 0 π / 4 d θ = 4 θ | 0 π / 4 = 4 ( π 4 ) = π {\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4}{1+x^{2}}}\;dx&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{1+\tan ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{\sec ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=4\theta {\Bigg |}_{0}^{\pi /4}\\&=4\left({\frac {\pi }{4}}\right)\\&=\pi \end{aligned}}} Caso III: Integrando conteniendo x 2 − a 2 {\displaystyle x^{2}-a^{2}} Se hace el cambio de variable x = a sec θ {\displaystyle x=a\sec \theta } identidad trigonométrica sec 2 ( θ ) − tan 2 ( θ ) = 1 {\displaystyle \sec ^{2}(\theta )-\tan ^{2}(\theta )=1}
Integral Indefinida Ejemplo I Construcción geométrica para Caso III {\displaystyle {\text{III}}} La integral
∫ d x x 2 − a 2 {\displaystyle \int {\frac {dx}{x^{2}-a^{2}}}} también puede ser evaluada utilizando fracciones parciales en lugar de utilizar sustitución trigonométrica. Sin embargo, la integral
∫ x 2 − a 2 d x {\displaystyle \int {\sqrt {x^{2}-a^{2}}}\,dx} no. En este caso, una sustitución apropiada es
x = a sec θ d x = a sec θ tan θ d θ θ = arcsec ( x a ) {\displaystyle {\begin{aligned}x&=a\sec \theta \\dx&=a\sec \theta \tan \theta \,d\theta \\\theta &=\operatorname {arcsec} \left({\frac {x}{a}}\right)\end{aligned}}} donde a > 0 {\displaystyle a>0} a 2 = a {\displaystyle {\sqrt {a^{2}}}=a}
0 ≤ θ < π 2 {\displaystyle 0\leq \theta <{\frac {\pi }{2}}} suponiendo que x > 0 {\displaystyle x>0} tan θ ≥ 0 {\displaystyle \tan \theta \geq 0} tan 2 θ = tan θ {\displaystyle {\sqrt {\tan ^{2}\theta }}=\tan \theta }
Entonces,
∫ x 2 − a 2 d x = ∫ a 2 sec 2 θ − a 2 ⋅ a sec θ tan θ d θ = ∫ a 2 ( sec 2 θ − 1 ) ⋅ a sec θ tan θ d θ = ∫ a 2 tan 2 θ ⋅ a sec θ tan θ d θ = ∫ a 2 sec θ tan 2 θ d θ = a 2 ∫ ( sec θ ) ( sec 2 θ − 1 ) d θ = a 2 ∫ ( sec 3 θ − sec θ ) d θ {\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&=\int {\sqrt {a^{2}\sec ^{2}\theta -a^{2}}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}(\sec ^{2}\theta -1)}}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int {\sqrt {a^{2}\tan ^{2}\theta }}\cdot a\sec \theta \tan \theta \,d\theta \\&=\int a^{2}\sec \theta \tan ^{2}\theta \,d\theta \\&=a^{2}\int (\sec \theta )(\sec ^{2}\theta -1)\,d\theta \\&=a^{2}\int (\sec ^{3}\theta -\sec \theta )\,d\theta \end{aligned}}} Uno puede evaluar la integral de la función secante multiplicando tanto el numerador como el denominador por ( sec θ + tan θ ) {\displaystyle (\sec \theta +\tan \theta )} [ 3]
∫ x 2 − a 2 d x = a 2 2 ( sec θ tan θ + ln | sec θ + tan θ | ) − a 2 ln | sec θ + tan θ | + C = a 2 2 ( sec θ tan θ − ln | sec θ + tan θ | ) + C = a 2 2 ( x a ⋅ x 2 a 2 − 1 − ln | x a + x 2 a 2 − 1 | ) + C = 1 2 ( x x 2 − a 2 − a 2 ln | x + x 2 − a 2 a | ) + C . {\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}} Sustituciones que eliminan funciones trigonométricas La sustitución de una nueva variable por una función trigonométrica en ocasiones puede ser usada para facilitar el cálculo de la integral, dejando el integrando sin funciones trigonométricas.
∫ f ( sen ( x ) , cos ( x ) ) d x = ∫ 1 ± 1 − u 2 f ( u , ± 1 − u 2 ) d u u = sen ( x ) ∫ f ( sen ( x ) , cos ( x ) ) d x = ∫ 1 ∓ 1 − u 2 f ( ± 1 − u 2 , u ) d u u = cos ( x ) ∫ f ( sen ( x ) , cos ( x ) ) d x = ∫ 2 1 + u 2 f ( 2 u 1 + u 2 , 1 − u 2 1 + u 2 ) d u u = tan ( x 2 ) {\displaystyle {\begin{aligned}\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}\;f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\operatorname {sen}(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}\;f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}\;f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\[6pt]\end{aligned}}} La última sustitución es conocida como la Sustitución de Weierstrass , que hace uso de las fórmulas de la tangente del ángulo mitad .
Ejemplo Considérese la integral
∫ 4 cos x ( 1 + cos x ) 3 d x {\displaystyle \int {\frac {4\cos x}{(1+\cos x)^{3}}}\;dx} Si utilizamos la sustitución de Weierstrass entonces
∫ 4 cos x ( 1 + cos x ) 3 d x = ∫ 2 1 + u 2 4 ( 1 − u 2 1 + u 2 ) ( 1 + 1 − u 2 1 + u 2 ) 3 d u = ∫ ( 1 − u 2 ) ( 1 + u 2 ) d u = ∫ ( 1 − u 4 ) d u = u − u 5 5 + C = tan ( x 2 ) − 1 5 tan 5 ( x 2 ) + C {\displaystyle {\begin{aligned}\int {\frac {4\cos x}{(1+\cos x)^{3}}}\,dx&=\int {\frac {2}{1+u^{2}}}{\frac {4\left({\frac {1-u^{2}}{1+u^{2}}}\right)}{\left(1+{\frac {1-u^{2}}{1+u^{2}}}\right)^{3}}}\,du\\&=\int (1-u^{2})(1+u^{2})\,du\\&=\int (1-u^{4})\,du\\&=u-{\frac {u^{5}}{5}}+C\\&=\tan \left({\frac {x}{2}}\right)-{\frac {1}{5}}\tan ^{5}\left({\frac {x}{2}}\right)+C\end{aligned}}} Sustitución hiperbólica También se pueden utilizar sustituciones mediante funciones hiperbólicas para simplificar determinadas integrales.[ 4]
Por ejemplo, en la integral
∫ 1 a 2 + x 2 d x {\displaystyle \int {\frac {1}{\sqrt {a^{2}+x^{2}}}}\,dx}
se realiza la sustitución x = a sinh u {\displaystyle x=a\sinh {u}} d x = a cosh u d u . {\displaystyle dx=a\cosh u\,du.}
Entonces, usando las identidades cosh 2 ( x ) − sinh 2 ( x ) = 1 {\displaystyle \cosh ^{2}(x)-\sinh ^{2}(x)=1} sinh − 1 x = ln ( x + x 2 + 1 ) , {\displaystyle \sinh ^{-1}{x}=\ln(x+{\sqrt {x^{2}+1}}),}
∫ 1 a 2 + x 2 d x = ∫ a cosh u a 2 + a 2 sinh 2 u d u = ∫ a cosh u a 1 + sinh 2 u d u = ∫ a cosh u a cosh u d u = u + C = sinh − 1 x a + C = ln ( x 2 a 2 + 1 + x a ) + C = ln ( x 2 + a 2 + x a ) + C {\displaystyle {\begin{aligned}\int {\frac {1}{\sqrt {a^{2}+x^{2}}}}\,dx&=\int {\frac {a\cosh u}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C\\[6pt]&=\ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\[6pt]&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{aligned}}}
Véase también Referencias ↑ Stewart, James (2008). Calculus: Early Transcendentals (6th edición). Brooks/Cole. ISBN 0-495-01166-5 ↑ Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th edición). Addison-Wesley . ISBN 0-321-58876-2 ↑ Stewart, James (2012). «Section 7.2: Trigonometric Integrals». Calculus - Early Transcendentals . United States: Cengage Learning. pp. 475-6. ISBN 978-0-538-49790-9 ↑ Boyadzhiev, Khristo N. «Hyperbolic Substitutions for Integrals». Archivado desde el original el 26 de febrero de 2020. Consultado el 4 de marzo de 2013 . Q1191963 


 Datos: Q1191963
Datos: Q1191963





![{\displaystyle {\begin{aligned}\int {\frac {dx}{\sqrt {a^{2}-x^{2}}}}&=\int {\frac {a\cos \theta }{\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}}\;d\theta \\[6pt]&=\int {\frac {a\cos \theta }{\sqrt {a^{2}\cos ^{2}\theta }}}\;d\theta \\[6pt]&=\int d\theta \\[6pt]&=\theta +C\\[6pt]&={\text{arcsen}}\left({\frac {x}{a}}\right)+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c33cee5a81fe5b1fc55154b51e4ebb497aa176b)





















![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}-x^{2}}}\,dx&=\int {\sqrt {a^{2}-a^{2}\operatorname {sen} ^{2}\theta }}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1-\operatorname {sen} ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(\cos ^{2}\theta )}}\,(a\cos \theta )\,d\theta \\[6pt]&=\int (a\cos \theta )(a\cos \theta )\,d\theta \\[6pt]&=a^{2}\int \cos ^{2}\theta \,d\theta \\[6pt]&=a^{2}\int \left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&={\frac {a^{2}}{2}}\left(\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right)+C\\[6pt]&={\frac {a^{2}}{2}}(\theta +\operatorname {sen} \theta \cos \theta )+C\\[6pt]&={\frac {a^{2}}{2}}\left({\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{a}}{\sqrt {1-{\frac {x^{2}}{a^{2}}}}}\right)+C\\[6pt]&={\frac {a^{2}}{2}}\;{\text{arcsen}}\left({\frac {x}{a}}\right)+{\frac {x}{2}}{\sqrt {a^{2}-x^{2}}}+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1d4616bf2e80282227306399174c44ba7787196)








![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\int _{-\pi /6}^{\pi /6}{\sqrt {4-4\operatorname {sen} ^{2}\theta }}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(1-\operatorname {sen} ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}{\sqrt {4(\cos ^{2}\theta )}}\,(2\cos \theta )\,d\theta \\[6pt]&=\int _{-\pi /6}^{\pi /6}(2\cos \theta )(2\cos \theta )\,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\cos ^{2}\theta \,d\theta \\[6pt]&=4\int _{-\pi /6}^{\pi /6}\left({\frac {1+\cos 2\theta }{2}}\right)\,d\theta \\[6pt]&=2\left[\theta +{\frac {1}{2}}\operatorname {sen} 2\theta \right]_{-\pi /6}^{\pi /6}\\[6pt]&=[2\theta +\operatorname {sen} 2\theta ]{\Biggl |}_{-\pi /6}^{\pi /6}\\[6pt]&=\left({\frac {\pi }{3}}+\operatorname {sen} {\frac {\pi }{3}}\right)-\left(-{\frac {\pi }{3}}+\operatorname {sen} \left(-{\frac {\pi }{3}}\right)\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bdb3b420d72073bb0cc67483388d2dd9e7d9b1c4)
![{\displaystyle {\begin{aligned}\int _{-1}^{1}{\sqrt {4-x^{2}}}\,dx&=\left[2\;{\text{arcsen}}\left({\frac {x}{2}}\right)+{\frac {x}{2}}{\sqrt {4-x^{2}}}\right]_{-1}^{1}\\[6pt]&=\left(2\;{\text{arcsen}}\left({\frac {1}{2}}\right)+{\frac {1}{2}}{\sqrt {3}}\right)-\left(2\;{\text{arcsen}}\left(-{\frac {1}{2}}\right)-{\frac {1}{2}}{\sqrt {3}}\right)\\[6pt]&=\left(2\cdot {\frac {\pi }{6}}+{\frac {\sqrt {3}}{2}}\right)-\left(2\cdot \left(-{\frac {\pi }{6}}\right)-{\frac {\sqrt {3}}{2}}\right)\\[6pt]&={\frac {2\pi }{3}}+{\sqrt {3}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a30c5d7cd0d8b39715021f705e76be11dcfa5e1)






![{\displaystyle {\begin{aligned}\int {\frac {dx}{a^{2}+x^{2}}}&=\int {\frac {a\sec ^{2}\theta }{a^{2}+a^{2}\tan ^{2}\theta }}\,d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}(1+\tan ^{2}\theta )}}\;d\theta \\[6pt]&=\int {\frac {a\sec ^{2}\theta }{a^{2}\sec ^{2}\theta }}\,d\theta \\[6pt]&={\frac {1}{a}}\int d\theta \\[6pt]&={\frac {\theta }{a}}+C\\[6pt]&={\frac {1}{a}}\arctan \left({\frac {x}{a}}\right)+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5b087324f1c492895eac14832e631d2478e8fff)






![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&=\int {\sqrt {a^{2}+a^{2}\tan ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}(1+\tan ^{2}\theta )}}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int {\sqrt {a^{2}\sec ^{2}\theta }}\,(a\sec ^{2}\theta )\,d\theta \\[6pt]&=\int (a\sec \theta )(a\sec ^{2}\theta )\,d\theta \\[6pt]&=a^{2}\int \sec ^{3}\theta \,d\theta .\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/108a5f1becea83b5cb41021d81544ff3e1bab889)
![{\displaystyle {\begin{aligned}\int {\sqrt {a^{2}+x^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\sqrt {1+{\frac {x^{2}}{a^{2}}}}}\cdot {\frac {x}{a}}+\ln \left|{\sqrt {1+{\frac {x^{2}}{a^{2}}}}}+{\frac {x}{a}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {a^{2}+x^{2}}}+a^{2}\ln \left|x+{\sqrt {a^{2}+x^{2}}}\right|\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b72bbed5d6bbb2d3dff666fda9985029351c25a)







![{\displaystyle {\begin{aligned}\int _{0}^{1}{\frac {4}{1+x^{2}}}\;dx&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{1+\tan ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}{\frac {\sec ^{2}\theta }{\sec ^{2}\theta }}\;d\theta \\[6pt]&=4\int _{0}^{\pi /4}d\theta \\[6pt]&=4\theta {\Bigg |}_{0}^{\pi /4}\\&=4\left({\frac {\pi }{4}}\right)\\&=\pi \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09938a7ac146b25472d7a851dd9a7d68b57de4df)












![{\displaystyle {\begin{aligned}\int {\sqrt {x^{2}-a^{2}}}\,dx&={\frac {a^{2}}{2}}(\sec \theta \tan \theta +\ln |\sec \theta +\tan \theta |)-a^{2}\ln |\sec \theta +\tan \theta |+C\\[6pt]&={\frac {a^{2}}{2}}(\sec \theta \tan \theta -\ln |\sec \theta +\tan \theta |)+C\\[6pt]&={\frac {a^{2}}{2}}\left({\frac {x}{a}}\cdot {\sqrt {{\frac {x^{2}}{a^{2}}}-1}}-\ln \left|{\frac {x}{a}}+{\sqrt {{\frac {x^{2}}{a^{2}}}-1}}\right|\right)+C\\[6pt]&={\frac {1}{2}}\left(x{\sqrt {x^{2}-a^{2}}}-a^{2}\ln \left|{\frac {x+{\sqrt {x^{2}-a^{2}}}}{a}}\right|\right)+C.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d551bea9f1a33df981d45ab8cf11a1443d6da85)
![{\displaystyle {\begin{aligned}\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\pm {\sqrt {1-u^{2}}}}}\;f\left(u,\pm {\sqrt {1-u^{2}}}\right)\,du&&u=\operatorname {sen}(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {1}{\mp {\sqrt {1-u^{2}}}}}\;f\left(\pm {\sqrt {1-u^{2}}},u\right)\,du&&u=\cos(x)\\[6pt]\int f(\operatorname {sen}(x),\cos(x))\,dx&=\int {\frac {2}{1+u^{2}}}\;f\left({\frac {2u}{1+u^{2}}},{\frac {1-u^{2}}{1+u^{2}}}\right)\,du&&u=\tan \left({\tfrac {x}{2}}\right)\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b07688dbf8f93a45c673360d666c378ecf2f09)







![{\displaystyle {\begin{aligned}\int {\frac {1}{\sqrt {a^{2}+x^{2}}}}\,dx&=\int {\frac {a\cosh u}{\sqrt {a^{2}+a^{2}\sinh ^{2}u}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a{\sqrt {1+\sinh ^{2}{u}}}}}\,du\\[6pt]&=\int {\frac {a\cosh {u}}{a\cosh u}}\,du\\[6pt]&=u+C\\[6pt]&=\sinh ^{-1}{\frac {x}{a}}+C\\[6pt]&=\ln \left({\sqrt {{\frac {x^{2}}{a^{2}}}+1}}+{\frac {x}{a}}\right)+C\\[6pt]&=\ln \left({\frac {{\sqrt {x^{2}+a^{2}}}+x}{a}}\right)+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4de72234865476739112fe15f4849d934ebb1622)










