Z-transform

In mathematics and signal processing, the Z-transform converts a discrete-time signal, which is a sequence of real or complex numbers, into a complex valued frequency-domain (the z-domain or z-plane) representation.^[1][2]

It can be considered a discrete-time equivalent of the Laplace transform (the s-domain or s-plane).^[3] This similarity is explored in the theory of time-scale calculus.

While the continuous-time Fourier transform is evaluated on the s-domain's vertical axis (the imaginary axis), the discrete-time Fourier transform is evaluated along the z-domain's unit circle. The s-domain's left half-plane maps to the area inside the z-domain's unit circle, while the s-domain's right half-plane maps to the area outside of the z-domain's unit circle.

One of the means of designing digital filters is to take analog designs, subject them to a bilinear transform which maps them from the s-domain to the z-domain, and then produce the digital filter by inspection, manipulation, or numerical approximation. Such methods tend not to be accurate except in the vicinity of the complex unity, i.e. at low frequencies.

History

The foundational concept now recognized as the Z-transform, which is a cornerstone in the analysis and design of digital control systems, was not entirely novel when it emerged in the mid-20th century. Its embryonic principles can be traced back to the work of the French mathematician Pierre-Simon Laplace, who is better known for the Laplace transform, a closely related mathematical technique. However, the explicit formulation and application of what we now understand as the Z-transform were significantly advanced in 1947 by Witold Hurewicz and colleagues. Their work was motivated by the challenges presented by sampled-data control systems, which were becoming increasingly relevant in the context of radar technology during that period. The Z-transform provided a systematic and effective method for solving linear difference equations with constant coefficients, which are ubiquitous in the analysis of discrete-time signals and systems.^[4][5]

The method was further refined and gained its official nomenclature, "the Z-transform," in 1952, thanks to the efforts of John R. Ragazzini and Lotfi A. Zadeh, who were part of the sampled-data control group at Columbia University. Their work not only solidified the mathematical framework of the Z-transform but also expanded its application scope, particularly in the field of electrical engineering and control systems.^[6][7]

The development of the Z-transform did not halt with Ragazzini and Zadeh. A notable extension, known as the modified or advanced Z-transform, was later introduced by Eliahu I. Jury. Jury's work extended the applicability and robustness of the Z-transform, especially in handling initial conditions and providing a more comprehensive framework for the analysis of digital control systems. This advanced formulation has played a pivotal role in the design and stability analysis of discrete-time control systems, contributing significantly to the field of digital signal processing.^[8][9]

Interestingly, the conceptual underpinnings of the Z-transform intersect with a broader mathematical concept known as the method of generating functions, a powerful tool in combinatorics and probability theory. This connection was hinted at as early as 1730 by Abraham de Moivre, a pioneering figure in the development of probability theory. De Moivre utilized generating functions to solve problems in probability, laying the groundwork for what would eventually evolve into the Z-transform. From a mathematical perspective, the Z-transform can be viewed as a specific instance of a Laurent series, where the sequence of numbers under investigation is interpreted as the coefficients in the (Laurent) expansion of an analytic function. This perspective not only highlights the deep mathematical roots of the Z-transform but also illustrates its versatility and broad applicability across different branches of mathematics and engineering.^[10]

Definition

The Z-transform can be defined as either a one-sided or two-sided transform. (Just like we have the one-sided Laplace transform and the two-sided Laplace transform.)^[11]

Bilateral Z-transform

The bilateral or two-sided Z-transform of a discrete-time signal ${\displaystyle x[n]}$ is the formal power series ${\displaystyle X(z)}$ defined as:

where ${\displaystyle n}$ is an integer and ${\displaystyle z}$ is, in general, a complex number. In polar form, ${\displaystyle z}$ may be written as:

${\displaystyle z=Ae^{j\phi }=A\cdot (\cos {\phi }+j\sin {\phi })}$

where ${\displaystyle A}$ is the magnitude of ${\displaystyle z}$, ${\displaystyle j}$ is the imaginary unit, and ${\displaystyle \phi }$ is the complex argument (also referred to as angle or phase) in radians.

Unilateral Z-transform

Alternatively, in cases where ${\displaystyle x[n]}$ is defined only for ${\displaystyle n\geq 0}$, the single-sided or unilateral Z-transform is defined as:

In signal processing, this definition can be used to evaluate the Z-transform of the unit impulse response of a discrete-time causal system.

An important example of the unilateral Z-transform is the probability-generating function, where the component ${\displaystyle x[n]}$ is the probability that a discrete random variable takes the value ${\displaystyle n}$, and the function ${\displaystyle X(z)}$ is usually written as ${\displaystyle X(s)}$ in terms of ${\displaystyle s=z^{-1}}$. The properties of Z-transforms (listed in § Properties) have useful interpretations in the context of probability theory.

Inverse Z-transform

The inverse Z-transform is:

where ${\displaystyle C}$ is a counterclockwise closed path encircling the origin and entirely in the region of convergence (ROC). In the case where the ROC is causal (see Example 2), this means the path ${\displaystyle C}$ must encircle all of the poles of ${\displaystyle X(z)}$.

A special case of this contour integral occurs when ${\displaystyle C}$ is the unit circle. This contour can be used when the ROC includes the unit circle, which is always guaranteed when ${\displaystyle X(z)}$ is stable, that is, when all the poles are inside the unit circle. With this contour, the inverse Z-transform simplifies to the inverse discrete-time Fourier transform, or Fourier series, of the periodic values of the Z-transform around the unit circle:

The Z-transform with a finite range of ${\displaystyle n}$ and a finite number of uniformly spaced ${\displaystyle z}$ values can be computed efficiently via Bluestein's FFT algorithm. The discrete-time Fourier transform (DTFT)—not to be confused with the discrete Fourier transform (DFT)—is a special case of such a Z-transform obtained by restricting ${\displaystyle z}$ to lie on the unit circle.

Region of convergence

The region of convergence (ROC) is the set of points in the complex plane for which the Z-transform summation converges (i.e. doesn't blow up in magnitude to infinity):

${\displaystyle \mathrm {ROC} =\left\{z:\left|\sum _{n=-\infty }^{\infty }x[n]z^{-n}\right|<\infty \right\}}$

Example 1 (no ROC)

Let ${\displaystyle x[n]=(.5)^{n}\ .}$ Expanding ${\displaystyle x[n]}$ on the interval ${\displaystyle (-\infty ,\infty )}$ it becomes

${\displaystyle x[n]=\left\{\dots ,(.5)^{-3},(.5)^{-2},(.5)^{-1},1,(.5),(.5)^{2},(.5)^{3},\dots \right\}=\left\{\dots ,2^{3},2^{2},2,1,(.5),(.5)^{2},(.5)^{3},\dots \right\}.}$

Looking at the sum

${\displaystyle \sum _{n=-\infty }^{\infty }x[n]z^{-n}\to \infty .}$

Therefore, there are no values of ${\displaystyle z}$ that satisfy this condition.

Example 2 (causal ROC)

Let ${\displaystyle x[n]=(.5)^{n}\,u[n]}$ (where ${\displaystyle u}$ is the Heaviside step function). Expanding ${\displaystyle x[n]}$ on the interval ${\displaystyle (-\infty ,\infty )}$ it becomes

${\displaystyle x[n]=\left\{\dots ,0,0,0,1,(.5),(.5)^{2},(.5)^{3},\dots \right\}.}$

Looking at the sum

${\displaystyle \sum _{n=-\infty }^{\infty }x[n]z^{-n}=\sum _{n=0}^{\infty }(.5)^{n}z^{-n}=\sum _{n=0}^{\infty }\left({\frac {.5}{z}}\right)^{n}={\frac {1}{1-(.5)z^{-1}}}.}$

The last equality arises from the infinite geometric series and the equality only holds if ${\displaystyle |(.5)z^{-1}|<1,}$ which can be rewritten in terms of ${\displaystyle z}$ as ${\displaystyle |z|>(.5).}$ Thus, the ROC is ${\displaystyle |z|>(.5).}$ In this case the ROC is the complex plane with a disc of radius 0.5 at the origin "punched out".

Example 3 (anti causal ROC)

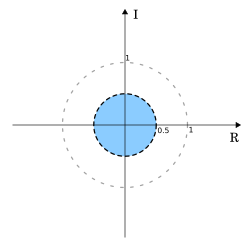
Let ${\displaystyle x[n]=-(.5)^{n}\,u[-n-1]}$ (where ${\displaystyle u}$ is the Heaviside step function). Expanding ${\displaystyle x[n]}$ on the interval ${\displaystyle (-\infty ,\infty )}$ it becomes

${\displaystyle x[n]=\left\{\dots ,-(.5)^{-3},-(.5)^{-2},-(.5)^{-1},0,0,0,0,\dots \right\}.}$

Looking at the sum

${\displaystyle {\begin{aligned}\sum _{n=-\infty }^{\infty }x[n]\,z^{-n}&=-\sum _{n=-\infty }^{-1}(.5)^{n}\,z^{-n}\\&=-\sum _{m=1}^{\infty }\left({\frac {z}{.5}}\right)^{m}\\&=-{\frac {(.5)^{-1}z}{1-(.5)^{-1}z}}\\&=-{\frac {1}{(.5)z^{-1}-1}}\\&={\frac {1}{1-(.5)z^{-1}}}\\\end{aligned}}}$

and using the infinite geometric series again, the equality only holds if ${\displaystyle |(.5)^{-1}z|<1}$ which can be rewritten in terms of ${\displaystyle z}$ as ${\displaystyle |z|<(.5).}$ Thus, the ROC is ${\displaystyle |z|<(.5).}$ In this case the ROC is a disc centered at the origin and of radius 0.5.

What differentiates this example from the previous example is only the ROC. This is intentional to demonstrate that the transform result alone is insufficient.

Examples conclusion

Examples 2 & 3 clearly show that the Z-transform ${\displaystyle X(z)}$ of ${\displaystyle x[n]}$ is unique when and only when specifying the ROC. Creating the pole–zero plot for the causal and anticausal case show that the ROC for either case does not include the pole that is at 0.5. This extends to cases with multiple poles: the ROC will never contain poles.

In example 2, the causal system yields a ROC that includes ${\displaystyle |z|=\infty }$ while the anticausal system in example 3 yields an ROC that includes ${\displaystyle |z|=0.}$

In systems with multiple poles it is possible to have a ROC that includes neither ${\displaystyle |z|=\infty }$ nor ${\displaystyle |z|=0.}$ The ROC creates a circular band. For example,

${\displaystyle x[n]=(.5)^{n}\,u[n]-(.75)^{n}\,u[-n-1]}$

has poles at 0.5 and 0.75. The ROC will be 0.5 < |z| < 0.75, which includes neither the origin nor infinity. Such a system is called a mixed-causality system as it contains a causal term ${\displaystyle (.5)^{n}\,u[n]}$ and an anticausal term ${\displaystyle -(.75)^{n}\,u[-n-1].}$

The stability of a system can also be determined by knowing the ROC alone. If the ROC contains the unit circle (i.e., |z| = 1) then the system is stable. In the above systems the causal system (Example 2) is stable because |z| > 0.5 contains the unit circle.

Let us assume we are provided a Z-transform of a system without a ROC (i.e., an ambiguous ${\displaystyle x[n]}$). We can determine a unique ${\displaystyle x[n]}$ provided we desire the following:

• Stability
• Causality

For stability the ROC must contain the unit circle. If we need a causal system then the ROC must contain infinity and the system function will be a right-sided sequence. If we need an anticausal system then the ROC must contain the origin and the system function will be a left-sided sequence. If we need both stability and causality, all the poles of the system function must be inside the unit circle.

The unique ${\displaystyle x[n]}$ can then be found.

Properties

Properties of the z-transform

Property	Time domain	Z-domain	Proof	ROC
Definition of Z-transform	${\displaystyle x[n]}$	${\displaystyle X(z)}$	${\displaystyle X(z)={\mathcal {Z}}\{x[n]\}}$ (definition of the z-transform) ${\displaystyle x[n]={\mathcal {Z}}^{-1}\{X(z)\}}$ (definition of the inverse z-transform)	${\displaystyle r_{2}<|z|<r_{1}}$
Linearity	${\displaystyle a_{1}x_{1}[n]+a_{2}x_{2}[n]}$	${\displaystyle a_{1}X_{1}(z)+a_{2}X_{2}(z)}$	${\displaystyle {\begin{aligned}X(z)&=\sum _{n=-\infty }^{\infty }(a_{1}x_{1}[n]+a_{2}x_{2}[n])z^{-n}\\&=a_{1}\sum _{n=-\infty }^{\infty }x_{1}[n]\,z^{-n}+a_{2}\sum _{n=-\infty }^{\infty }x_{2}[n]\,z^{-n}\\&=a_{1}X_{1}(z)+a_{2}X_{2}(z)\end{aligned}}}$	Contains ROC1 ∩ ROC2
Time expansion	${\displaystyle x_{K}[n]={\begin{cases}x[r],&n=Kr\\0,&n\notin K\mathbb {Z} \end{cases}}}$ with ${\displaystyle K\mathbb {Z} :=\{Kr:r\in \mathbb {Z} \}}$	${\displaystyle X(z^{K})}$	${\displaystyle {\begin{aligned}X_{K}(z)&=\sum _{n=-\infty }^{\infty }x_{K}[n]z^{-n}\\&=\sum _{r=-\infty }^{\infty }x[r]z^{-rK}\\&=\sum _{r=-\infty }^{\infty }x[r](z^{K})^{-r}\\&=X(z^{K})\end{aligned}}}$	${\displaystyle R^{\frac {1}{K}}}$
Decimation	${\displaystyle x[Kn]}$	${\displaystyle {\frac {1}{K}}\sum _{p=0}^{K-1}X\left(z^{\tfrac {1}{K}}\cdot e^{-i{\tfrac {2\pi }{K}}p}\right)}$	ohio-state.edu or ee.ic.ac.uk
Time delay	${\displaystyle x[n-k]}$ with ${\displaystyle k>0}$ and ${\displaystyle x:x[n]=0\ \forall \,n<0}$	${\displaystyle z^{-k}X(z)}$	${\displaystyle {\begin{aligned}{\mathcal {Z}}\{x[n-k]\}&=\sum _{n=0}^{\infty }x[n-k]z^{-n}\\&=\sum _{j=-k}^{\infty }x[j]z^{-(j+k)}&&j=n-k\\&=\sum _{j=-k}^{\infty }x[j]z^{-j}z^{-k}\\&=z^{-k}\sum _{j=-k}^{\infty }x[j]z^{-j}\\&=z^{-k}\sum _{j=0}^{\infty }x[j]z^{-j}&&x[\beta ]=0,\beta <0\\&=z^{-k}X(z)\end{aligned}}}$	ROC, except ${\displaystyle z{=}0}$ if ${\displaystyle k>0}$ and ${\displaystyle z{=}\infty }$ if ${\displaystyle k<0}$
Time advance	${\displaystyle x[n+k]}$ with ${\displaystyle k>0}$	Bilateral Z-transform: $${\displaystyle z^{k}X(z)}$$ Unilateral Z-transform:[12] $${\displaystyle z^{k}\,X(z)-z^{k}\sum _{n=0}^{k-1}x[n]\,z^{-n}}$$
First difference backward	${\displaystyle x[n]-x[n-1]}$ with ${\displaystyle x[n]{=}0}$ for ${\displaystyle n<0}$	${\displaystyle (1-z^{-1})\,X(z)}$		Contains the intersection of ROC of ${\displaystyle X_{1}(z)}$ and ${\displaystyle z\neq 0}$
First difference forward	${\displaystyle x[n+1]-x[n]}$	${\displaystyle (z-1)\,X(z)-z\,x[0]}$
Time reversal	${\displaystyle x[-n]}$	${\displaystyle X(z^{-1})}$	${\displaystyle {\begin{aligned}{\mathcal {Z}}\{x(-n)\}&=\sum _{n=-\infty }^{\infty }x[-n]z^{-n}\\&=\sum _{m=-\infty }^{\infty }x[m]z^{m}\\&=\sum _{m=-\infty }^{\infty }x[m]{(z^{-1})}^{-m}\\&=X(z^{-1})\\\end{aligned}}}$	${\displaystyle {\tfrac {1}{r_{1}}}<|z|<{\tfrac {1}{r_{2}}}}$
Scaling in the z-domain	${\displaystyle a^{n}x[n]}$	${\displaystyle X(a^{-1}z)}$	${\displaystyle {\begin{aligned}{\mathcal {Z}}\left\{a^{n}x[n]\right\}&=\sum _{n=-\infty }^{\infty }a^{n}x[n]z^{-n}\\&=\sum _{n=-\infty }^{\infty }x[n](a^{-1}z)^{-n}\\&=X(a^{-1}z)\end{aligned}}}$	${\displaystyle |a|r_{2}<|z|<|a|r_{1}}$
Complex conjugation	${\displaystyle x^{*}[n]}$	${\displaystyle X^{*}(z^{*})}$	${\displaystyle {\begin{aligned}{\mathcal {Z}}\{x^{*}(n)\}&=\sum _{n=-\infty }^{\infty }x^{*}[n]z^{-n}\\&=\sum _{n=-\infty }^{\infty }\left[x[n](z^{*})^{-n}\right]^{*}\\&=\left[\sum _{n=-\infty }^{\infty }x[n](z^{*})^{-n}\right]^{*}\\&=X^{*}(z^{*})\end{aligned}}}$
Real part	${\displaystyle \operatorname {Re} \{x[n]\}}$	${\displaystyle {\tfrac {1}{2}}\left[X(z)+X^{*}(z^{*})\right]}$
Imaginary part	${\displaystyle \operatorname {Im} \{x[n]\}}$	${\displaystyle {\tfrac {1}{2j}}\left[X(z)-X^{*}(z^{*})\right]}$
Differentiation in the z-domain	${\displaystyle n\,x[n]}$	${\displaystyle -z{\frac {dX(z)}{dz}}}$	${\displaystyle {\begin{aligned}{\mathcal {Z}}\{n\,x(n)\}&=\sum _{n=-\infty }^{\infty }n\,x[n]z^{-n}\\&=z\sum _{n=-\infty }^{\infty }n\,x[n]z^{-n-1}\\&=-z\sum _{n=-\infty }^{\infty }x[n](-n\,z^{-n-1})\\&=-z\sum _{n=-\infty }^{\infty }x[n]{\frac {d}{dz}}(z^{-n})\\&=-z{\frac {dX(z)}{dz}}\end{aligned}}}$	ROC, if ${\displaystyle X(z)}$ is rational; ROC possibly excluding the boundary, if ${\displaystyle X(z)}$ is irrational[13]
Convolution	${\displaystyle x_{1}[n]*x_{2}[n]}$	${\displaystyle X_{1}(z)\,X_{2}(z)}$	${\displaystyle {\begin{aligned}{\mathcal {Z}}\{x_{1}(n)*x_{2}(n)\}&={\mathcal {Z}}\left\{\sum _{l=-\infty }^{\infty }x_{1}[l]x_{2}[n-l]\right\}\\&=\sum _{n=-\infty }^{\infty }\left[\sum _{l=-\infty }^{\infty }x_{1}(l)x_{2}[n-l]\right]z^{-n}\\&=\sum _{l=-\infty }^{\infty }x_{1}[l]\left[\sum _{n=-\infty }^{\infty }x_{2}[n-l]z^{-n}\right]\\&=\left[\sum _{l=-\infty }^{\infty }x_{1}(l)z^{-l}\right]\!\!\left[\sum _{n=-\infty }^{\infty }x_{2}[n]z^{-n}\right]\\&=X_{1}(z)X_{2}(z)\end{aligned}}}$	Contains ROC1 ∩ ROC2
Cross-correlation	${\displaystyle r_{x_{1},x_{2}}=x_{1}^{*}[-n]*x_{2}[n]}$	${\displaystyle R_{x_{1},x_{2}}(z)=X_{1}^{*}({\tfrac {1}{z^{*}}})X_{2}(z)}$		Contains the intersection of ROC of ${\displaystyle X_{1}({\tfrac {1}{z^{*}}})}$ and ${\displaystyle X_{2}(z)}$
Accumulation	${\displaystyle \sum _{k=-\infty }^{n}x[k]}$	${\displaystyle {\frac {1}{1-z^{-1}}}X(z)}$	${\displaystyle {\begin{aligned}\sum _{n=-\infty }^{\infty }\sum _{k=-\infty }^{n}x[k]z^{-n}&=\sum _{n=-\infty }^{\infty }(x[n]+\cdots )z^{-n}\\&=X(z)\left(1+z^{-1}+z^{-2}+\cdots \right)\\&=X(z)\sum _{j=0}^{\infty }z^{-j}\\&=X(z){\frac {1}{1-z^{-1}}}\end{aligned}}}$
Multiplication	${\displaystyle x_{1}[n]\,x_{2}[n]}$	${\displaystyle {\frac {1}{j2\pi }}\oint _{C}X_{1}(v)X_{2}({\tfrac {z}{v}})v^{-1}\mathrm {d} v}$		-

Parseval's theorem

${\displaystyle \sum _{n=-\infty }^{\infty }x_{1}[n]x_{2}^{*}[n]\quad =\quad {\frac {1}{j2\pi }}\oint _{C}X_{1}(v)X_{2}^{*}({\tfrac {1}{v^{*}}})v^{-1}\mathrm {d} v}$

Initial value theorem: If ${\displaystyle x[n]}$ is causal, then

${\displaystyle x[0]=\lim _{z\to \infty }X(z).}$

Final value theorem: If the poles of ${\displaystyle (z-1)X(z)}$ are inside the unit circle, then

${\displaystyle x[\infty ]=\lim _{z\to 1}(z-1)X(z).}$

Table of common Z-transform pairs

Here:

${\displaystyle u:n\mapsto u[n]={\begin{cases}1,&n\geq 0\\0,&n<0\end{cases}}}$

is the unit (or Heaviside) step function and

${\displaystyle \delta :n\mapsto \delta [n]={\begin{cases}1,&n=0\\0,&n\neq 0\end{cases}}}$

is the discrete-time unit impulse function (cf Dirac delta function which is a continuous-time version). The two functions are chosen together so that the unit step function is the accumulation (running total) of the unit impulse function.

	Signal, ${\displaystyle x[n]}$	Z-transform, ${\displaystyle X(z)}$	ROC
1	${\displaystyle \delta [n]}$	1	all z
2	${\displaystyle \delta [n-n_{0}]}$	${\displaystyle z^{-n_{0}}}$	${\displaystyle z\neq 0}$
3	${\displaystyle u[n]\,}$	${\displaystyle {\frac {1}{1-z^{-1}}}}$	${\displaystyle |z|>1}$
4	${\displaystyle -u[-n-1]}$	${\displaystyle {\frac {1}{1-z^{-1}}}}$	${\displaystyle |z|<1}$
5	${\displaystyle nu[n]}$	${\displaystyle {\frac {z^{-1}}{(1-z^{-1})^{2}}}}$	${\displaystyle |z|>1}$
6	${\displaystyle -nu[-n-1]\,}$	${\displaystyle {\frac {z^{-1}}{(1-z^{-1})^{2}}}}$	${\displaystyle |z|<1}$
7	${\displaystyle n^{2}u[n]}$	${\displaystyle {\frac {z^{-1}(1+z^{-1})}{(1-z^{-1})^{3}}}}$	${\displaystyle |z|>1\,}$
8	${\displaystyle -n^{2}u[-n-1]\,}$	${\displaystyle {\frac {z^{-1}(1+z^{-1})}{(1-z^{-1})^{3}}}}$	${\displaystyle |z|<1\,}$
9	${\displaystyle n^{3}u[n]}$	${\displaystyle {\frac {z^{-1}(1+4z^{-1}+z^{-2})}{(1-z^{-1})^{4}}}}$	${\displaystyle |z|>1\,}$
10	${\displaystyle -n^{3}u[-n-1]}$	${\displaystyle {\frac {z^{-1}(1+4z^{-1}+z^{-2})}{(1-z^{-1})^{4}}}}$	${\displaystyle |z|<1\,}$
11	${\displaystyle a^{n}u[n]}$	${\displaystyle {\frac {1}{1-az^{-1}}}}$	${\displaystyle |z|>|a|}$
12	${\displaystyle -a^{n}u[-n-1]}$	${\displaystyle {\frac {1}{1-az^{-1}}}}$	${\displaystyle |z|<|a|}$
13	${\displaystyle na^{n}u[n]}$	${\displaystyle {\frac {az^{-1}}{(1-az^{-1})^{2}}}}$	${\displaystyle |z|>|a|}$
14	${\displaystyle -na^{n}u[-n-1]}$	${\displaystyle {\frac {az^{-1}}{(1-az^{-1})^{2}}}}$	${\displaystyle |z|<|a|}$
15	${\displaystyle n^{2}a^{n}u[n]}$	${\displaystyle {\frac {az^{-1}(1+az^{-1})}{(1-az^{-1})^{3}}}}$	${\displaystyle |z|>|a|}$
16	${\displaystyle -n^{2}a^{n}u[-n-1]}$	${\displaystyle {\frac {az^{-1}(1+az^{-1})}{(1-az^{-1})^{3}}}}$	${\displaystyle |z|<|a|}$
17	${\displaystyle \left({\begin{array}{c}n+m-1\\m-1\end{array}}\right)a^{n}u[n]}$	${\displaystyle {\frac {1}{(1-az^{-1})^{m}}}}$, for positive integer ${\displaystyle m}$[13]	${\displaystyle |z|>|a|}$
18	${\displaystyle (-1)^{m}\left({\begin{array}{c}-n-1\\m-1\end{array}}\right)a^{n}u[-n-m]}$	${\displaystyle {\frac {1}{(1-az^{-1})^{m}}}}$, for positive integer ${\displaystyle m}$[13]	${\displaystyle |z|<|a|}$
19	${\displaystyle \cos(\omega _{0}n)u[n]}$	${\displaystyle {\frac {1-z^{-1}\cos(\omega _{0})}{1-2z^{-1}\cos(\omega _{0})+z^{-2}}}}$	${\displaystyle |z|>1}$
20	${\displaystyle \sin(\omega _{0}n)u[n]}$	${\displaystyle {\frac {z^{-1}\sin(\omega _{0})}{1-2z^{-1}\cos(\omega _{0})+z^{-2}}}}$	${\displaystyle |z|>1}$
21	${\displaystyle a^{n}\cos(\omega _{0}n)u[n]}$	${\displaystyle {\frac {1-az^{-1}\cos(\omega _{0})}{1-2az^{-1}\cos(\omega _{0})+a^{2}z^{-2}}}}$	${\displaystyle |z|>|a|}$
22	${\displaystyle a^{n}\sin(\omega _{0}n)u[n]}$	${\displaystyle {\frac {az^{-1}\sin(\omega _{0})}{1-2az^{-1}\cos(\omega _{0})+a^{2}z^{-2}}}}$	${\displaystyle |z|>|a|}$

Relationship to Fourier series and Fourier transform

For values of ${\displaystyle z}$ in the region ${\displaystyle |z|{=}1}$, known as the unit circle, we can express the transform as a function of a single real variable ${\displaystyle \omega }$ by defining ${\displaystyle z{=}e^{j\omega }.}$ And the bi-lateral transform reduces to a Fourier series:

${\displaystyle \sum _{n=-\infty }^{\infty }x[n]\ z^{-n}=\sum _{n=-\infty }^{\infty }x[n]\ e^{-j\omega n},}$

(Eq.4)

which is also known as the discrete-time Fourier transform (DTFT) of the ${\displaystyle x[n]}$ sequence. This ${\displaystyle 2\pi }$-periodic function is the periodic summation of a Fourier transform, which makes it a widely used analysis tool. To understand this, let ${\displaystyle X(f)}$ be the Fourier transform of any function, ${\displaystyle x(t)}$, whose samples at some interval ${\displaystyle T}$ equal the ${\displaystyle x[n]}$ sequence. Then the DTFT of the ${\displaystyle x[n]}$ sequence can be written as follows.

${\displaystyle \underbrace {\sum _{n=-\infty }^{\infty }\overbrace {x(nT)} ^{x[n]}\ e^{-j2\pi fnT}} _{\text{DTFT}}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }X(f-k/T),}$

(Eq.5)

where ${\displaystyle T}$ has units of seconds, ${\displaystyle f}$ has units of hertz. Comparison of the two series reveals that ${\displaystyle \omega {=}2\pi fT}$ is a normalized frequency with unit of radian per sample. The value ${\displaystyle \omega {=}2\pi }$ corresponds to ${\textstyle f{=}{\frac {1}{T}}}$. And now, with the substitution ${\textstyle f{=}{\frac {\omega }{2\pi T}},}$ Eq.4 can be expressed in terms of ${\displaystyle X({\tfrac {\omega -2\pi k}{2\pi T}})}$(a Fourier transform):

${\displaystyle \sum _{n=-\infty }^{\infty }x[n]\ e^{-j\omega n}={\frac {1}{T}}\sum _{k=-\infty }^{\infty }\underbrace {X\left({\tfrac {\omega }{2\pi T}}-{\tfrac {k}{T}}\right)} _{X\left({\frac {\omega -2\pi k}{2\pi T}}\right)}.}$

(Eq.6)

As parameter T changes, the individual terms of Eq.5 move farther apart or closer together along the f-axis. In Eq.6 however, the centers remain 2π apart, while their widths expand or contract. When sequence ${\displaystyle x(nT)}$ represents the impulse response of an LTI system, these functions are also known as its frequency response. When the ${\displaystyle x(nT)}$ sequence is periodic, its DTFT is divergent at one or more harmonic frequencies, and zero at all other frequencies. This is often represented by the use of amplitude-variant Dirac delta functions at the harmonic frequencies. Due to periodicity, there are only a finite number of unique amplitudes, which are readily computed by the much simpler discrete Fourier transform (DFT). (See Discrete-time Fourier transform § Periodic data.)

Relationship to Laplace transform

Bilinear transform

The bilinear transform can be used to convert continuous-time filters (represented in the Laplace domain) into discrete-time filters (represented in the Z-domain), and vice versa. The following substitution is used:

${\displaystyle s={\frac {2}{T}}{\frac {(z-1)}{(z+1)}}}$

to convert some function ${\displaystyle H(s)}$ in the Laplace domain to a function ${\displaystyle H(z)}$ in the Z-domain (Tustin transformation), or

${\displaystyle z=e^{sT}\approx {\frac {1+sT/2}{1-sT/2}}}$

from the Z-domain to the Laplace domain. Through the bilinear transformation, the complex s-plane (of the Laplace transform) is mapped to the complex z-plane (of the z-transform). While this mapping is (necessarily) nonlinear, it is useful in that it maps the entire ${\displaystyle j\omega }$ axis of the s-plane onto the unit circle in the z-plane. As such, the Fourier transform (which is the Laplace transform evaluated on the ${\displaystyle j\omega }$ axis) becomes the discrete-time Fourier transform. This assumes that the Fourier transform exists; i.e., that the ${\displaystyle j\omega }$ axis is in the region of convergence of the Laplace transform.

Starred transform

Given a one-sided Z-transform ${\displaystyle X(z)}$ of a time-sampled function, the corresponding starred transform produces a Laplace transform and restores the dependence on ${\displaystyle T}$ (the sampling parameter):

${\displaystyle {\bigg .}X^{*}(s)=X(z){\bigg |}_{\displaystyle z=e^{sT}}}$

The inverse Laplace transform is a mathematical abstraction known as an impulse-sampled function.

Linear constant-coefficient difference equation

The linear constant-coefficient difference (LCCD) equation is a representation for a linear system based on the autoregressive moving-average equation:

${\displaystyle \sum _{p=0}^{N}y[n-p]\alpha _{p}=\sum _{q=0}^{M}x[n-q]\beta _{q}.}$

Both sides of the above equation can be divided by ${\displaystyle \alpha _{0}}$ if it is not zero. By normalizing with ${\displaystyle \alpha _{0}{=}1,}$ the LCCD equation can be written

${\displaystyle y[n]=\sum _{q=0}^{M}x[n-q]\beta _{q}-\sum _{p=1}^{N}y[n-p]\alpha _{p}.}$

This form of the LCCD equation is favorable to make it more explicit that the "current" output ${\displaystyle y[n]}$ is a function of past outputs ${\displaystyle y[n-p],}$ current input ${\displaystyle x[n],}$ and previous inputs ${\displaystyle x[n-q].}$

Transfer function

Taking the Z-transform of the above equation (using linearity and time-shifting laws) yields:

${\displaystyle Y(z)\sum _{p=0}^{N}z^{-p}\alpha _{p}=X(z)\sum _{q=0}^{M}z^{-q}\beta _{q}}$

where ${\displaystyle X(z)}$ and ${\displaystyle Y(z)}$ are the z-transform of ${\displaystyle x[n]}$ and ${\displaystyle y[n],}$ respectively. (Notation conventions typically use capitalized letters to refer to the z-transform of a signal denoted by a corresponding lower case letter, similar to the convention used for notating Laplace transforms.)

Rearranging results in the system's transfer function:

${\displaystyle H(z)={\frac {Y(z)}{X(z)}}={\frac {\sum _{q=0}^{M}z^{-q}\beta _{q}}{\sum _{p=0}^{N}z^{-p}\alpha _{p}}}={\frac {\beta _{0}+z^{-1}\beta _{1}+z^{-2}\beta _{2}+\cdots +z^{-M}\beta _{M}}{\alpha _{0}+z^{-1}\alpha _{1}+z^{-2}\alpha _{2}+\cdots +z^{-N}\alpha _{N}}}.}$

Zeros and poles

From the fundamental theorem of algebra the numerator has ${\displaystyle M}$ roots (corresponding to zeros of ${\displaystyle H}$) and the denominator has ${\displaystyle N}$ roots (corresponding to poles). Rewriting the transfer function in terms of zeros and poles

${\displaystyle H(z)={\frac {(1-q_{1}z^{-1})(1-q_{2}z^{-1})\cdots (1-q_{M}z^{-1})}{(1-p_{1}z^{-1})(1-p_{2}z^{-1})\cdots (1-p_{N}z^{-1})}},}$

where ${\displaystyle q_{k}}$ is the ${\displaystyle k^{\text{th}}}$ zero and ${\displaystyle p_{k}}$ is the ${\displaystyle k^{\text{th}}}$ pole. The zeros and poles are commonly complex and when plotted on the complex plane (z-plane) it is called the pole–zero plot.

In addition, there may also exist zeros and poles at ${\displaystyle z{=}0}$ and ${\displaystyle z{=}\infty .}$ If we take these poles and zeros as well as multiple-order zeros and poles into consideration, the number of zeros and poles are always equal.

By factoring the denominator, partial fraction decomposition can be used, which can then be transformed back to the time domain. Doing so would result in the impulse response and the linear constant coefficient difference equation of the system.

Output response

If such a system ${\displaystyle H(z)}$ is driven by a signal ${\displaystyle X(z)}$ then the output is ${\displaystyle Y(z)=H(z)X(z).}$ By performing partial fraction decomposition on ${\displaystyle Y(z)}$ and then taking the inverse Z-transform the output ${\displaystyle y[n]}$ can be found. In practice, it is often useful to fractionally decompose ${\displaystyle \textstyle {\frac {Y(z)}{z}}}$ before multiplying that quantity by ${\displaystyle z}$ to generate a form of ${\displaystyle Y(z)}$ which has terms with easily computable inverse Z-transforms.

See also

• Advanced Z-transform
• Bilinear transform
• Difference equation (recurrence relation)
• Discrete convolution
• Discrete-time Fourier transform
• Finite impulse response
• Formal power series
• Generating function
• Generating function transformation
• Laplace transform
• Laurent series
• Least-squares spectral analysis
• Probability-generating function
• Star transform
• Zak transform
• Zeta function regularization

References

Further reading

• Refaat El Attar, Lecture notes on Z-Transform, Lulu Press, Morrisville NC, 2005. ISBN 1-4116-1979-X.
• Ogata, Katsuhiko, Discrete Time Control Systems 2nd Ed, Prentice-Hall Inc, 1995, 1987. ISBN 0-13-034281-5.
• Alan V. Oppenheim and Ronald W. Schafer (1999). Discrete-Time Signal Processing, 2nd Edition, Prentice Hall Signal Processing Series. ISBN 0-13-754920-2.

External links

• "Z-transform". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
• Merrikh-Bayat, Farshad (2014). "Two Methods for Numerical Inversion of the Z-Transform". arXiv:1409.1727 [math.NA].
• Z-Transform table of some common Laplace transforms
• Mathworld's entry on the Z-transform
• Z-Transform threads in Comp.DSP
• A graphic of the relationship between Laplace transform s-plane to Z-plane of the Z transform
• A video-based explanation of the Z-Transform for engineers
• What is the z-Transform?