Periodic summation

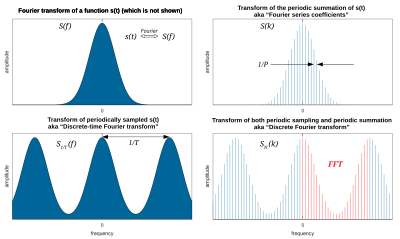
Sum of a function's values every _P_ offsets

In mathematics, any integrable function $s(t)$ can be made into a periodic function $s_{P}(t)$ with period P by summing the translations of the function $s(t)$ by integer multiples of P. This is called periodic summation:

s_{P}(t)=\sum _{n=-\infty }^{\infty }s(t+nP)

When $s_{P}(t)$ is alternatively represented as a Fourier series, the Fourier coefficients are equal to the values of the continuous Fourier transform, $S(f)\triangleq {\mathcal {F}}\{s(t)\},$ at intervals of ${\tfrac {1}{P}}$ .^[1]^[2] That identity is a form of the Poisson summation formula. Similarly, a Fourier series whose coefficients are samples of $s(t)$ at constant intervals (T) is equivalent to a periodic summation of $S(f),$ which is known as a discrete-time Fourier transform.

The periodic summation of a Dirac delta function is the Dirac comb. Likewise, the periodic summation of an integrable function is its convolution with the Dirac comb.

Quotient space as domain

If a periodic function is instead represented using the quotient space domain $\mathbb {R} /(P\mathbb {Z} )$ then one can write:

\varphi _{P}:\mathbb {R} /(P\mathbb {Z} )\to \mathbb {R}

\varphi _{P}(x)=\sum _{\tau \in x}s(\tau )~.

The arguments of $\varphi _{P}$ are equivalence classes of real numbers that share the same fractional part when divided by $P$ .

Citations

^ Pinsky, Mark (2001). Introduction to Fourier Analysis and Wavelets. Brooks/Cole. ISBN 978-0534376604.
^ Zygmund, Antoni (1988). Trigonometric Series (2nd ed.). Cambridge University Press. ISBN 978-0521358859.