Z-Transformation

Die z-Transformation ist ein mathematisches Verfahren der Systemtheorie zur Behandlung und Berechnung von kontinuierlich (zyklisch) abgetasteten Signalen und linearen zeitinvarianten zeitdiskreten dynamischen Systemen. Sie ist aus der Laplace-Transformation entstanden und hat auch ähnliche Eigenschaften und Berechnungsregeln. Die z-Transformation gilt für Signale im diskreten Zeitbereich (Wertefolgen), während die Laplace-Transformation für entsprechende Berechnungen im kontinuierlichen Zeitbereich dient. (Bezüglich des Zusammenhangs zwischen z-Transformation und Laplace-Transformation siehe auch: Matched-z-Transformation.)

Ein Vorteil der Anwendung der z-Transformation ergibt sich, wenn eine Wertefolge und eine systembeschreibende Differenzengleichung in eine algebraisch zusammengefasste z-Übertragungsfunktion überführt wird. Die z-Übertragungsfunktion dient der Systemanalyse, d. h. der Analyse des Systemverhalten bei verschiedenen Anregungen und insbesondere auch der Stabilitätsanalyse. Der Verlauf der Systemausgangsgröße ${\displaystyle y_{(k)}}$ kann bei gegebener Eingangsgröße ${\displaystyle u_{(k)}}$ durch verschiedene Methoden der inversen z-Transformation in den zeitdiskreten Bereich ${\displaystyle f_{(k)}}$ und dann im Zeitbereich ${\displaystyle f(t)}$ dargestellt werden.

Die z-Transformation wird größtenteils für die digitale Steuer- und Regelungstechnik und zur Berechnung digitaler Filter angewendet. Man kann sie aber auch zur Gewinnung von expliziten Formeln für rekursiv definierte Zahlenfolgen einsetzen.

Einführung in die z-Transformation

Geschichtliche Entwicklung

Die grundsätzlichen Ideen zur z-Transformation gehen auf Pierre-Simon Laplace zurück und wurden 1947 von Witold Hurewicz zur Lösung von linearen Differentialgleichungen mit konstanten Koeffizienten verwendet.^{[Einzelnachweise 1]}

Ursprünglich wurde sie als „Laplace-Transformation von Abtastfunktionen“ eingeführt, im Jahr 1952 erfolgte die heute übliche Begriffsfestlegung z-Transformation durch John R. Ragazzini und Lotfi A. Zadeh bei Arbeiten mit zeitdiskreten Daten im Rahmen der Regelungstechnik an der Columbia University.^{[Einzelnachweise 2][Einzelnachweise 3]}

Die Modifizierte z-Transformation geht auf Arbeiten von Eliahu Ibrahim Jury aus dem Jahr 1958 zurück.^{[Einzelnachweise 4]}

Bedeutung der z-Transformation und Anwendung

Der z-Bereich ist eine abstrakte mathematische Welt, die eine Reihe von Eigenschaften hat, die bei Untersuchungen von Systemeigenschaften sehr hilfreich ist (Zitat: Vorlesungsskript Uni Wien).

Abgetastete Signale werden benötigt, wenn Computer zeitinvariante dynamische Systeme und Signale zeitdiskret in Form von Differenzengleichungen berechnen sollen. Dabei geht es meist um die Anwendung für die digitale Regelung und Regelstrecken.

Abgetastete Signale im Abstand ${\displaystyle x(k\cdot T_{\mathrm {A} })}$ können mit Hilfe der z-Transformation mathematisch definiert werden. Die zeitkontinuierliche Beschreibung des abgetasteten Signals als modulierte Impulsfolgen mit ${\displaystyle k=(0,1,2,3,\dots )}$ stellt nur eine mathematische Modellvorstellung dar. Die unendlich hohen und schmalen Dirac-Impulse existieren in Wirklichkeit nicht. In der Realität müssen die zeitlichen Abtastfolgen sehr klein im Verhältnis der Systemzeitkonstanten liegen, anderenfalls wird das Rechenergebnis ungenau. Die rekursiven Differenzengleichungen bilden nur Annäherungen an eine gewünschte Originalfunktion.

Die z-Transformation hat für diskrete Systeme dieselbe Bedeutung, wie die Laplace-Transformation für kontinuierliche Systeme. Das Verständnis der Anwendung der z-Transformation im Gegensatz zur Laplace-Transformation ist ungleich schwieriger, weil die Abtastung bei Einsatz von Mikrocomputern eine Ein-Ausgangshardware mit Zeitverhalten darstellt. Für die Beschreibung dynamischer Systeme z. B. bei Reglern zur Parametrisierung müssen Regelstrecken identifiziert und Differenzengleichungen gebildet werden.

Die Anwendung der z-Transformation erleichtert die Prozedur der Berechnung der zeitdiskreten Signalfolgen mit Differenzengleichungen zu z-Übertragungsfunktionen. Diese werden mit inverser z-Transformation zurück vom z-Bereich in den k-Bereich der abgetasteten Signale transformiert und liefern damit als Ausgangsgröße Signalfolgen im diskreten Zeitbereich.

Mit Hilfe der z-Transformation können aus systembeschreibenden Differenzengleichungen mit zeitdiskreten Signalen zu z-Übertragungsfunktionen als gebrochen rationale Funktionen berechnet werden, die – ähnlich bei der Laplace-Transformation – durch Pole und Nullstellen das Systemverhalten identifizieren. Damit sind algebraische Operationen mit anderen z-transformierten Systemen und z-transformierten Signalen möglich.

Gleichungen und Eigenschaften der z-Transformation

Die häufig verwendeten z-Transformationsbeziehungen zwischen dem k- und z-Bereich werden in Tabellenform dargestellt und erleichtern damit die Berechnungen (siehe #Tabelle der Korrespondenzen des Zeitbereichs f(t), des Laplace- und z-Bereichs (Auszüge)).

Definitionen der verwendeten Variablen und Parameter:

${\displaystyle X(z)}$ = Signal im Bildbereich; ${\displaystyle z}$ = z-Variable; ${\displaystyle T_{\mathrm {A} }}$ = Abtastzeit, ${\displaystyle k}$ = Abtastfolge = Nummerierung eines Folgegliedes, ${\displaystyle n}$ = Zahl bestimmter Abtastschritte, z. B. bei Verschiebungen.

Bilaterale z-Transformation

Die bilaterale z-Transformation eines Signals ${\displaystyle x[k]}$ ist die formale Laurent-Reihe ${\displaystyle X(z)}$:

${\displaystyle X(z)=Z\{x[k]\}=\sum _{k=-\infty }^{\infty }x[k]z^{-k}}$,

wobei ${\displaystyle k}$ alle ganzen Zahlen durchläuft und ${\displaystyle z}$ im Allgemeinen eine komplexe Zahl der Form:

${\displaystyle z=A\mathrm {e} ^{\mathrm {j} \varphi }=\sigma +\mathrm {j} \omega }$

ist. ${\displaystyle A}$ ist der Betrag von ${\displaystyle z}$ und ${\displaystyle \varphi }$ der Winkel der komplexen Zahl in Polarkoordinaten. Alternativ kann ${\displaystyle z}$ auch in kartesischer Form als Realteil ${\displaystyle \sigma }$ und Imaginärteil ${\displaystyle \omega }$ beschrieben werden.

Unter gewissen Konvergenzbedingungen ist die z-Transformierte eine holomorphe Funktion auf einem Kreisring in der komplexen Zahlenebene, unter schwächeren Bedingungen immerhin noch eine quadratintegrierbare Funktion auf dem Einheitskreis.

Unilaterale z-Transformation

Substituiert man in der Beschreibung einer Abtastfolge im Laplace-Bereich den Ausdruck ${\displaystyle \mathrm {e} ^{sT_{\mathrm {A} }}}$ durch ${\displaystyle z}$, so erhält man eine Potenzreihe in ${\displaystyle z}$:

${\displaystyle \sum _{k=0}^{\infty }x[k]\mathrm {e} ^{-skT}=\sum _{k=0}^{\infty }x[k]\cdot z^{-k}=x(0)+x(1)\cdot z^{-1}+x(2)\cdot z^{-2}+\cdots }$

Dabei ist

${\displaystyle z=\mathrm {e} ^{sT_{\mathrm {A} }}}$

Wenn ${\displaystyle x[k]}$ nur nichtnegative ${\displaystyle k}$ Werte hat, kann die unilaterale z-Transformation definiert werden:

${\displaystyle X(z)=Z\{x[k]\}=\sum _{k=0}^{\infty }x[k]\cdot z^{-k}}$

In der Signalverarbeitung wird die unilaterale z-Transformation für kausale Signale verwendet.

Eigenschaften wie Linearität, Verschiebung, Faltung, Differentiation

• Linearität. Die z-Transformierte von zwei linear verknüpften Signalen ist die lineare Verknüpfung der beiden z-transformierten Signale.

${\displaystyle Z({a_{1}x_{1}[k]+a_{2}x_{2}[k]})=a_{1}Z({x_{1}[k]})+a_{2}Z({x_{2}[k]})\!}$

• Verschiebung. Wird das Signal im Zeitbereich um n nach rechts verschoben, so muss die z-Transformierte mit ${\displaystyle z^{-n}}$ multipliziert werden. Bei der Verschiebung nach links kommen noch weitere Terme hinzu.

${\displaystyle Z({x[k-n]})=z^{-n}Z({x[k]})\!}$

${\displaystyle Z({x[k+n]})=z^{n}\left(Z({x[k]})-\sum _{i=0}^{n-1}x[i]z^{-i}\right)}$

• Faltung. Die Faltung von zwei Signalen im Zeitbereich entspricht dem Produkt im Frequenzbereich.

${\displaystyle Z({x[k]}*{y[k]})=Z({x[k]})Z({y[k]})\!}$

• Differentiation .

${\displaystyle Z({kx[k]})=-z{\frac {\partial Z({x[k]})}{\partial z}}}$

Zusätzliche Eigenschaften der unilateralen z-Transformation

Es sei ${\displaystyle f_{k}=f(k)}$ und ${\displaystyle F(z)}$ deren z-Transformierte. Weiter sei folgende Schreibweise für die Transformation der diskreten Zeitfunktion in die Bildebene definiert.

${\displaystyle f_{k}\circ \!\!-\!\!\bullet F(z)}$

Dann gelten folgende Regeln:

${\displaystyle {\begin{array}{llcl}{\text{Verschiebungssatz}}&f_{k-n}&\circ \!\!-\!\!\bullet &z^{-n}F(z)\\&f_{k+n}&\circ \!\!-\!\!\bullet &z^{n}(F(z)-\sum _{i=0}^{n-1}f_{i}z^{-i})\\&f_{k+1}&\circ \!\!-\!\!\bullet &z^{1}(F(z)-f_{0})\\&f_{k+2}&\circ \!\!-\!\!\bullet &z^{2}(F(z)-f_{0}-f_{1}z^{-1})\\{\text{Dämpfungssatz}}&a^{-k}\cdot f_{k}&\circ \!\!-\!\!\bullet &F(a\cdot z)\\{\text{Ableitung der Bildfunktion}}&k\cdot f_{k}&\circ \!\!-\!\!\bullet &-z{\frac {\mathrm {d} F(z)}{\mathrm {d} z}}\\{\text{Spektraler}}&W(z)&=&U(z)\cdot V(z)\\{\text{Multiplikationssatz}}&w_{k}&=&\sum _{n=0}^{k}u_{k-n}\cdot v_{n}=\sum _{n=0}^{k}u_{n}\cdot v_{k-n}\\{\text{Differenzensatz}}&\Delta f_{k}&=&f_{k+1}-f_{k}\\&\Delta ^{2}f_{k}&=&\Delta f_{k+1}-\Delta f_{k}=f_{k+2}-2f_{k+1}+f_{k}\\&\Delta ^{2}f_{k}&\circ \!\!-\!\!\bullet &(z-1)^{2}F(z)-z((z-1)f_{0}+\Delta f_{0})\\&\Delta ^{n}f_{k}&\circ \!\!-\!\!\bullet &(z-1)^{n}F(z)-z\sum _{i=0}^{n-1}(z-1)^{n-i-1}\Delta ^{i}f_{0}\\{\text{Summensatz}}&\sum _{n=0}^{k}f_{n}&\circ \!\!-\!\!\bullet &z{\frac {F(z)}{z-1}}\\{\text{1. Grenzwertsatz}}&f_{n}&=&\lim _{z\to \infty }z^{n}\cdot (F(z)-\sum _{k=0}^{n-1}z^{-k}f_{k})\\&f_{0}&=&\lim _{z\to \infty }F(z)\\{\text{2. Grenzwertsatz}}&\lim _{k\to \infty }f_{k}&=&\lim _{z\to 1}(z-1)F(z)\\{\text{Stabilität}}&|z_{PK}|<1&&\rightarrow {\text{asymptotische Stabilität}}\end{array}}}$

Inverse z-Transformation

Die inverse z-Transformation kann mit der Formel

${\displaystyle x[k]=Z^{-1}\{X(z)\}\,=\,{\frac {1}{2\pi \mathrm {i} }}\oint _{C}X(z)z^{k-1}\mathrm {d} z\ }$

berechnet werden, wobei C eine beliebige geschlossene Kurve um den Ursprung ist, die im Konvergenzbereich von ${\displaystyle X(z)}$ liegt.

Die (unilaterale) z-Transformation ist zeitdiskret und entspricht der Laplace-Transformation für zeitkontinuierliche Signale.

Inverse unilaterale z-Transformation

Voraussetzungen: F(z) ist holomorph in einem Gebiet ${\displaystyle |z|>R}$ und ${\displaystyle \lim _{z\to \infty }F(z)<\infty }$.

Mit Residuum

${\displaystyle f(0)=\lim _{z\to \infty }F(z)}$,

${\displaystyle f(kT)=\sum _{i=1}^{m}\operatorname {Res} _{z=z_{i}}(F(z)z^{k-1})}$ für ${\displaystyle k\geq 1}$

Mit Laurent-Reihe

Der Integrand ${\displaystyle F(z)\cdot z^{k-1}}$ wird in eine Laurent-Reihe entwickelt. Die Zeitfunktion ist dann der Koeffizient −1 der Laurent Reihe, also ${\displaystyle f(k\tau )=A_{-1}}$.

Bei der Entwicklung in eine Reihe sind der binomische Lehrsatz und grundlegende Eigenschaften der Binomialkoeffizienten nützlich.

Beispiel 1

${\displaystyle {\frac {z^{k}}{z-1}}\,=\,{\frac {(1+(z-1))^{k}}{z-1}}\,=\,\sum _{n=0}^{k}{k \choose n}1^{k-n}(z-1)^{n-1}\,=\,\sum _{n=-1}^{k-1}{k-1 \choose n+1}1^{k-n}(z-1)^{n}}$,

${\displaystyle A_{-1}\,=\,{k-1 \choose 0}\cdot 1^{k-1}(z-1)^{0}\,=\,1}$.

Beispiel 2

${\displaystyle {\frac {\mathrm {e} ^{zt}}{z-a}}\,=\,{\frac {\mathrm {e} ^{at}}{z-a}}\sum _{n=0}^{\infty }{\frac {((z-a)t)^{n}}{n!}}\,=\,\mathrm {e} ^{at}\sum _{n=0}^{\infty }{\frac {(z-a)^{n-1}\cdot t^{n}}{n!}}}$,

${\displaystyle A_{-1}\,=\,\mathrm {e} ^{at}{\frac {t^{0}}{0!}}\,=\,\mathrm {e} ^{at}}$.

Bei wesentlicher Singularität

${\displaystyle f(k\tau )\,=\,{\frac {1}{k!}}\cdot \left({\frac {\mathrm {d} ^{n}}{\mathrm {d} z^{k}}}f(1/z)\right)_{z=0}}$.

Grundlagen der z-Transformation

Die z-Transformation ist ein mathematisches Verfahren der Systemtheorie zur Behandlung und Berechnung von kontinuierlich abgetasteten Signalen und linearen zeitinvarianten zeitdiskreten dynamischen Systemen. Ein zeitdiskretes dynamisches System wird durch Differenzengleichungen oder als z-Transformierte beschrieben. Im Gegensatz dazu wird die Laplace-Transformation für kontinuierlichen Signale und Systeme verwendet.

Definition der Formelzeichen und Systemgrößen nachfolgender Systemdarstellungen

Liste der wichtigsten Formelzeichen und Systemgrößen, die im Folgenden verwendet werden:

Formelzeichen	Erklärung	Bemerkung
${\displaystyle u(t)}$	Eingangssignal	Werden in der Regelungstechnik Regler und Regelstrecke gleichzeitig betrachtet, wird die Eingangsgröße des Reglers als ${\displaystyle e(t)}$ (Regelabweichung) bezeichnet. Die Ausgangsgröße des Reglers ${\displaystyle u(t)}$ ist dann gleichzeitig die Eingangsgröße der Regelstrecke.
${\displaystyle y(t)}$	Ausgangssignal	meist Systemantwort, bei Regelkreisen die Regelgröße.
Kleinbuchstaben	Zeitbereich	z. B.: f, u, y
Großbuchstaben	Bildbereich	z. B.: F, U, Y, G
${\displaystyle {T_{\mathrm {A} }},\ {\text{auch}}\ T_{0},\ T}$	Abtastzeit	Zeitlicher Abstand der Abtastungen eines zeitdiskreten Signals. Mit der Frequenz ${\displaystyle f\ =1/{T_{\mathrm {A} }}}$ wird ein kontinuierliches Signal abgetastet.
${\displaystyle \Delta t}$	Zeitintervall	${\displaystyle \Delta t}$ ist ein Parameter der diskreten Zeit, keine reale Zeit. In Verbindung mit Abtastung kann ${\displaystyle \Delta t=T_{\mathrm {A} }}$ sein. ${\displaystyle \Delta t}$ wird z. B. bei der Berechnung der Differenzengleichungen verwendet.
${\displaystyle k}$	Abtastfolge	${\displaystyle k=(0,1,2,3,\dots ,\infty )}$ in einer unendlichen oder ${\displaystyle k=(0,1,2,3,\dots ,k_{\mathrm {max} })}$ einer endlichen Folge. ${\displaystyle k}$ wird auch für die Nummerierung der Werte in einer Folge verwendet.
${\displaystyle n,\ auch\ d}$	Abtastschritte	${\displaystyle n=d={\text{Anzahl zusammenhängender Abtastschritte}}}$. (n ist auch eine Bezeichnung für die Potenz der s-Variablen eines Nennerpolynoms)
${\displaystyle f_{(k)}}$	Wertefolge	Eine Folge der Werte: ${\displaystyle f_{(k)}=[f(0),f(T_{\mathrm {A} }),f(2T_{\mathrm {A} }),f(3T_{\mathrm {A} }),\dots ]}$
${\displaystyle f(t)}$	Signal im Zeitbereich	Zeitsignal (allgemein)
${\displaystyle f(k\cdot T_{\mathrm {A} })}$	Zeitdiskretes Signal	Wert des Signals ${\displaystyle f(t)}$ zum Zeitpunkt ${\displaystyle k\cdot T_{\mathrm {A} }}$. Vereinfachte Schreibweise ist z. B. ${\displaystyle u_{(k)}}$ oder ${\displaystyle y_{(k)}}$.
${\displaystyle s=\sigma +\mathrm {i} \omega }$	Laplace Variable
e	Eulersche Zahl	e = Eulersche Zahl ≈ 2,71828.
${\displaystyle F(s)}$	Laplace-Transformiert	Laplace-Transformiertes Signal für kontinuierliche Systeme: Polynomfunktion mit Zählergrad: ${\displaystyle m}$ und Nennergrad: ${\displaystyle n}$
${\displaystyle G(s)={\frac {Y(s)}{U(s)}}}$	Laplace-Transformiert	Laplace-Übertragungsfunktion für kontinuierliche Systeme: Polynomfunktion mit Zählergrad: ${\displaystyle m}$ und Nennergrad: ${\displaystyle n}$
${\displaystyle z=\mathrm {e} ^{T_{\mathrm {A} }\cdot s}}$	z-Variable
${\displaystyle F(z)}$, ${\displaystyle G(z)}$	z-transformiert	z-transformiertes Signal bzw. z-Übertragungsfunktion für diskrete Systeme: Polynomfunktion mit Zählergrad: ${\displaystyle m}$ und Nennergrad: ${\displaystyle n}$
${\displaystyle T}$	Zeitkonstante	Zeitkonstante eines dynamischen Systems. Bei mehreren Zeitkonstanten des dynamischen Systems werden die Zeitkonstanten indiziert: ${\displaystyle T_{i}}$

Vergleich der diskreten und der kontinuierlichen Übertragungssysteme

Vergleich	diskretes System	kontinuierliches System
Eigenschaften der betrachteten Systeme	Linear, zeitinvariant, dynamisch Mindestens ein Eingangssignal ${\displaystyle u(t)}$ und ein Ausgangssignal ${\displaystyle y(t)}$
Ein-/Ausgangssignal	reelle Folge, Zeitreihe mit fortlaufendem konstanten Zeitintervalls ${\displaystyle T_{\mathrm {A} }}$	kontinuierliches reelles Signal
Systembeschreibung im Zeitbereich	Differenzengleichung	gewöhnliche Differentialgleichungen
Transformation in den Bildbereich	mit z-Transformation	mit Laplace-Transformation
Operator-Schreibweise der Transformation	${\displaystyle F(z)={\mathcal {Z}}\{f_{(k)}\}}$	${\displaystyle F(s)={\mathcal {L}}\{f(t)\}}$
Inverse Transformation	${\displaystyle f_{(k)}={\mathcal {Z}}^{-1}\{F(z)\}}$	${\displaystyle f(t)={\mathcal {L}}^{-1}\{F(s)\}}$
Systembeschreibung im Bildbereich	z-Übertragungsfunktion	s-Übertragungsfunktion
Allgemeine Eigenschaften im Bildbereich: Beziehung der Stabilität in der z-Ebene. Stabilität: Pole im Inneren des z-Einheitskreises. Grenzstabilität: Pole auf der z-Kreislinie.	Polstellenanalyse für Übertragungsfunktionen G(s), G(z). Die Übertragungsfunktion wird im Bildbereich als Bruch mit Zähler- und Nennerpolynom dargestellt. Übertragungsfunktion = Ausgangssignal / Eingangssignal = Zählerpolynom / Nennerpolynom Die Auswertung des Nennerpolynoms führt zu Aussagen über die Stabilität des Systems. Stabilitätsgebiet „linke s-Halbebene“ wird in das Innere eines Einheitskreises der z-Ebene transformiert. Einheitskreis mit Radius 1, Ordinate = Imaginärteil von z, Abszisse = Realteil von z. Ablesung: Stabilität, Grenzstabilität, bei Instabilität liegen die Pole außerhalb des Einheitskreises.

Grundlagen Differenzengleichungen für lineare zeitinvariante Systeme

Für die numerische Berechnung des Systemverhaltens eines zeitdiskreten dynamischen Systems können Differenzengleichungen ${\displaystyle y_{(k)}=f({\text{Systemparameter}},k,k-1,\Delta t,u_{(k)})}$ verwendet werden. Mit ihrer Hilfe lässt sich das Systemverhalten (der Verlauf der Systemausgangsgröße ${\displaystyle y(t)}$ ) für ein gegebenes Eingangssignal ${\displaystyle u(t)}$ im zeitdiskreten Bereich ${\displaystyle f(k\Delta t)}$ berechnen.

Differenzengleichungen entstehen meist aus systembeschreibenden gewöhnlichen Differenzialgleichungen, deren Differentialquotienten durch Differenzenquotienten ersetzt werden. Die kontinuierlichen mathematischen Operationen der Integration und Differentiation werden zeitdiskret durch Summen- und Differenzenbildung angenähert.

Die Differenzengleichungen beschreiben mit dem Approximationsalgorithmus für ein kleines Zeitintervall ${\displaystyle \Delta t}$ die Signaländerungen nach jedem Zeitintervall als Funktion des betreffenden Teilsystems (Linearfaktoren im s-Bereich) und des Eingangssignals. Mit der fortlaufenden Wiederholung der Berechnung mit dem Zeitintervall ${\displaystyle \Delta t}$ und Addition der Änderungsergebnisse zum vorherigen Ergebnis ergibt sich der Signalverlauf eines Systems über die Zeit ${\displaystyle k_{\mathrm {max} }\cdot \Delta t}$.

Es bestehen verschiedene mathematische Verfahren, zeitkontinuierliche Systeme in zeitdiskrete Systeme zu beschreiben und umzuwandeln.

Differenzengleichungen der einfachsten Art beziehen sich auf die den Linearfaktoren der Übertragungsfunktion ${\displaystyle G(s)}$ zugehörigen Differenzialgleichungen erster Ordnung, deren Differentialquotienten durch Differenzenquotienten ersetzt werden. Diese Beziehung ist von großer Bedeutung, weil nur 4 verschiedene Typen von Differenzengleichungen erster Ordnung existieren, mit denen alle Formen von linearen Übertragungssystemen gebildet werden können, auch solche mit Schwingungsanteilen mit konjugiert komplexen Polen oder Nullstellen. Diese Teilsysteme können beliebig multiplikativ, additiv, zurück gekoppelt oder strukturell vermascht sein und gelten sowohl für den s-Bereich wie auch im diskreten Zeitbereich.

Meistens wird zur Aufstellung der Differenzengleichungen das Euler-Streckenzugverfahren nach dem Rückwärts- oder Vorwärts-Differenzenquotienten als einfachstes numerisches Verfahren verwendet. Nach diesem Verfahren können aus den zugehörigen Differenzialgleichungen der 4 Elementarsysteme erster Ordnung der Übertragungsfunktionen ${\displaystyle G(s)}$ Differenzengleichungen gebildet werden, indem z. B. an Stelle des Differenzialquotienten mit ${\displaystyle \mathrm {d} y/\mathrm {d} t}$ der Rückwärts-Differenzenquotient

${\displaystyle {\frac {\Delta y}{\Delta t}}={\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}}$

näherungsweise eingeführt wird.

In der Regel wird davon ausgegangen, dass die inneren Systemspeicher des Übertragungssystems sich im Ruhezustand befinden und die Anfangswerte bei ${\displaystyle t=0}$ für ${\displaystyle y_{(0)}=0}$ und alle Ableitungen von ${\displaystyle y_{(0)}}$ Null sind.

Beispiel der Entwicklung der Differenzengleichung der Integration (I-Glied) aus der Differenzialgleichung:

Die Übertragungsfunktion des I-Gliedes lautet: ${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{T_{I}\cdot s}}.}$ Die zugehörige Differenzialgleichung lautet: ${\displaystyle T_{I}\cdot {\dot {y}}(t)=u(t).}$ Der Differenzenquotient wird an Stelle des Differenzialquotienten ${\displaystyle {\dot {y}}(t)}$ eingesetzt. Anstelle der kontinuierlichen Systemgrößen ${\displaystyle y(t)}$ und ${\displaystyle u(t)}$ treten die aktuellen zeitdiskreten Werte ${\displaystyle y(k\Delta t)=y_{(k)}}$ und ${\displaystyle u(k\Delta t)=u_{(k)}}$: ${\displaystyle T_{I}\cdot {\frac {y_{(k)}-y_{(k-1)}}{\Delta t}}=u_{(k)}.}$ Damit lautet die nach ${\displaystyle y_{(k)}}$ umgestellte Differenzengleichung des I-Gliedes: ${\displaystyle y_{(k)}=y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T_{I}}}}$ In gleicher Weise können die Differenzengleichungen von Systemen erster Ordnung aus den zugehörigen Differenzialgleichungen abgeleitet werden.

Tabelle der Differenzengleichungen (Euler-Rückwärts) der Elementarsysteme G(s) erster Ordnung

Elementarsysteme	P-Glied	I-Glied	D-Glied	PD1-Glied	PT1-Glied
Übertragungsfunktion	${\displaystyle {\frac {Y}{U}}(s)=K}$	${\displaystyle {\frac {Y}{U}}(s)={\frac {1}{T\cdot s}}}$	${\displaystyle {\frac {Y}{U}}(s)=T\cdot s}$	${\displaystyle {\frac {Y}{U}}(s)=K\cdot (T\cdot s+1)}$	${\displaystyle {\frac {Y}{U}}(s)={\frac {K}{T\cdot s+1}}}$
Differenzengleichungen ${\displaystyle y_{(k)}=\,}$	${\displaystyle K\cdot u_{(k)}}$	${\displaystyle y_{(k-1)}+u_{(k)}\cdot {\frac {\Delta t}{T}}}$	${\displaystyle [u_{(k)}-u_{(k-1)}]\cdot {\frac {T}{\Delta t}}}$	${\displaystyle K_{PD1}\cdot \left[u_{(k)}+(u_{(k)}-u_{(k-1)})\cdot {\frac {T}{\Delta t}}\right]}$	${\displaystyle y_{(k-1)}+[K_{PT1}\cdot u_{(k)}-y_{(k-1)}]\cdot {\frac {\Delta t}{T+\Delta t}}}$

(Mit ${\displaystyle K}$ = Verstärkungsfaktor, ${\displaystyle y_{(k)}}$ = aktuelle Ausgangsgröße, ${\displaystyle y_{(k-1)}}$ = vorherige Ausgangsgröße, ${\displaystyle T}$ = Zeitkonstante, ${\displaystyle u_{(k)}}$ = aktuelle Eingangsgröße)

Die einmalige Anwendung einer Differenzengleichung ${\displaystyle y_{(k)}=f(T,\Delta t,k,k-1,u_{(k)})}$ zum Zeitpunkt ${\displaystyle k\cdot \Delta t}$ ergibt für eine gegebene Eingangsfolge ${\displaystyle u_{(k)}}$ ein Folgeglied der Ausgangsfolge ${\displaystyle y_{(k)}}$. Jedes Folgeglied ${\displaystyle y_{(k)}}$ bezieht sich auf eine zurückliegende Folge ${\displaystyle y_{(k-1)}}$. Deshalb wird eine solche Differenzengleichung als Rekursionsgleichung bezeichnet, weil jedes Folgeglied eine Funktion des vorherigen Folgegliedes ist.

Die rekursive Anwendung von Differenzengleichungen zur Berechnung von Eingangs-Wertefolgen zu Ausgangs-Wertefolgen bedeutet die angenäherte Lösung der systembeschreibenden Differentialgleichung des Systemausgangssignals ${\displaystyle y_{(k)}}$ von Wertefolgen (Berechnungspunkten) ${\displaystyle y_{(k)}=y(0),y(1),y(2),y(3),\dots }$.

Mit Hilfe eines Personal Computers kann das Systemverhalten eines dynamischen Systems oder eines Regelkreises mit Differenzengleichungen vollständig simuliert werden. Dabei wird eine endliche Anzahl ${\displaystyle k_{\mathrm {max} }}$ von Berechnungsfolgen (Wertefolgen) festgelegt und die Rechenergebnisse der Teilsysteme – das Systemverhalten – tabellarisch und grafisch als Berechnungspunkte im Abstand ${\displaystyle \Delta t}$ dargestellt. Die Differenzengleichung enthält bereits die Lösungsvorschrift der Systemausgangsgröße in Annäherung an die systembeschreibende Differentialgleichung.

Handelt es sich bei dem dynamischen System um eine Hardware mit einer im zeitlichen Abstand ${\displaystyle T_{\mathrm {A} }}$ abgetasteten Eingangsfolge ${\displaystyle u_{(k)}}$, die über einen Mikrocomputer mit Differenzengleichungen zu einer Ausgangsfolge ${\displaystyle y_{(k)}}$ berechnet wird, kann mit Hilfe eines Haltegliedes eine treppenförmig gestufte quasi kontinuierliche Ausgangsgröße y(t) als Beispiel der prinzipiellen Funktion eines digitalen Reglers erreicht werden. Regelstrecken liegen in der Praxis meist als kontinuierliche Systeme vor, die eine kontinuierliche Stellgröße benötigen.

Differenzengleichungen höherer Ordnung

Differenzengleichungen können auch aus gewöhnlichen Differenzialgleichungen höherer Ordnung entwickelt werden, wenn ab dem Zeitpunkt ${\displaystyle t=kT_{\mathrm {A} }\geq 0}$ die letzten vergangenen Ausgangs-Wertefolgen mit ${\displaystyle k=[-1\to -n]}$ und die Eingangs-Wertefolgen mit ${\displaystyle k=[-1\to -m]}$ bekannt sind.

Zeitkontinuierliche lineare Systeme werden im Zeitbereich durch die gewöhnlichen Differenzialgleichungen ${\displaystyle n}$-ter Ordnung mit konstanten Koeffizienten für ${\displaystyle n\geq m}$ beschrieben. Dabei sind ${\displaystyle n}$ und ${\displaystyle m}$ die höchsten Ableitungen der Ausgangssignale ${\displaystyle y(t)}$ und Eingangssignale ${\displaystyle u(t)}$.

Eine gegebene gewöhnliche Differentialgleichung wird durch den Koeffizienten ${\displaystyle a_{0}}$ dividiert, um ${\displaystyle y(t)}$ freistellen zu können. Diese Form der Differentialgleichung wird entsprechend der dargestellten Koeffizienten wie folgt neu geordnet.

${\displaystyle y(t)+a_{1}{\dot {y}}(t)+a_{2}{\ddot {y}}(t)+\dots +a_{n}y^{(n)}(t)=b_{0}u(t)+b_{1}{\dot {u}}(t)+b_{2}{\ddot {u}}(t)+\dots +b_{m}u^{(m)}(t)}$.

Diese Differentialgleichung kann in eine Differenzengleichung überführt werden:

• ${\displaystyle f(kT_{\mathrm {A} })}$ wird vereinfacht als ${\displaystyle f_{(k)}}$ geschrieben und entspricht einem aktuellen Folgeglied.
• Die kontinuierlichen Systemgrößen ${\displaystyle y(t)\to y_{(k)}}$ und ${\displaystyle u(t)\to u_{(k)}}$ werden zeitdiskret dargestellt.
• Die Ableitungen im Zeitbereich ${\displaystyle \mathrm {d} y/\mathrm {d} t}$ werden entsprechend der Ordnung durch Differenzenquotienten ${\displaystyle \Delta y/\Delta t}$ der zugehörigen Ordnung ersetzt.

Jede Ableitung der Systemgrößen wird im zeitdiskreten Bereich entsprechend der Ordnung als zurückliegende Folgeglieder der Eingangs- und Ausgangsfolgen k-1 bis k-n oder k-m berücksichtigt.

Daraus folgt die Differenzengleichung:

${\displaystyle {y_{(k)}+a_{1}\cdot y_{(k-1)}+a_{2}\cdot y_{(k-2)}+\dots +a_{n}\cdot y_{(k-n)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dots +b_{m}\cdot u_{(k-m)}}}$.

Damit kann die allgemeine Form der Differenzengleichung nach ${\displaystyle y_{(k)}}$ aufgelöst werden:

${\displaystyle {y_{(k)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dots +b_{m}\cdot u_{(k-m)}-a_{1}\cdot y_{(k-1)}-a_{2}\cdot y_{(k-2)}-\dots -a_{n}\cdot y_{(k-n)}}}$.

Für die numerische Berechnung eines dynamischen Systems wird die s-Übertragungsfunktion oder die zugehörige Differentialgleichung benötigt. Die Umsetzung einer systembeschreibenden Differentialgleichung in eine angenäherte Differenzengleichung zur Beschreibung von Eingangsfolgen und Ausgangsfolgen eines dynamischen Systems wird ermöglicht, wenn die Differentiale der Differentialgleichung durch Rückwärts-Differenzenquotienten über die Abtastperiode ersetzt werden.^{[Einzelnachweise 5]}

Die folgenden Ableitungen der Differentialquotienten in Differenzenquotienten der 1. 2. und 3. Ordnung sind gegeben:

Differenzenquotient 1. Ordnung:

${\displaystyle {\dot {y}}(t)={\frac {\mathrm {d} y}{\mathrm {d} t}}\approx {\frac {\Delta y}{\Delta t}}={\frac {\Delta y_{k}}{T_{\mathrm {A} }}}={\frac {y_{(k)}-y_{(k-1)}}{T_{\mathrm {A} }}}}$

Der Differenzenquotient 2. Ordnung entsteht aus Differenzen der Differenz:

${\displaystyle {\ddot {y}}(t)={\frac {\mathrm {d} ^{2}y}{\mathrm {d} t^{2}}}\approx {\frac {\Delta ^{2}y_{k}}{T_{\mathrm {A} }^{2}}}={\frac {y_{(k)}-2y_{(k-1)}+y_{(k-2)}}{T_{\mathrm {A} }^{2}}}}$

Der Differenzenquotient 3. Ordnung lautet:

${\displaystyle y^{(3)}(t)={\frac {\mathrm {d} ^{3}y}{\mathrm {d} t^{3}}}\approx {\frac {\Delta ^{3}y_{k}}{T_{\mathrm {A} }^{3}}}={\frac {y_{(k)}-3y_{(k-1)}+3y_{(k-2)}-y_{(k-3)}}{T_{\mathrm {A} }^{3}}}}$

Nach erfolgtem Einsetzen der Differenzenquotienten in die Differenzengleichung eines dynamischen Systems lassen sich die neuen Koeffizienten aus den Koeffizienten der Differentialgleichung berechnen.

Beispiel der Entwicklung einer Differenzengleichung zur Berechnung der Sprungantwort eines ${\displaystyle PT_{2kk}}$-Gliedes mit konjugiert komplexen Polen:

Gegeben: Übertragungsfunktion im s-Bereich: ${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {1}{0{,}25s^{2}+0{,}125s+1}}}$ Sprungfunktion: u(t)=1 Gesucht: Differenzengleichung ${\displaystyle y_{(k)}}$ zur numerischen Bestimmung des System-Zeitverhaltens. Zugehörige Differentialgleichung nach dem Differentiationssatz der Laplace-Transformation: ${\displaystyle 0{,}25{\ddot {y}}(t)+0{,}125{\dot {y}}(t)+y(t)=u(t)}$ Die Differenzenquotienten für ${\displaystyle {\ddot {y}}(t)}$ und ${\displaystyle {\dot {y}}(t)}$ werden in die nachfolgende Differenzengleichung eingesetzt: ${\displaystyle 0{,}25\cdot {\frac {y_{(k)}-2y_{(k-1)}+y_{(k-2)}}{T_{\mathrm {A} }^{2}}}+0{,}125\cdot {\frac {y_{(k)}-y_{(k-1)}}{T_{\mathrm {A} }}}+y_{k}=u_{k}\quad |\qquad y(t)\to y_{(k)};\ u(t)\to u_{(k)}.}$ Die Brüche werden in einzelne additive Terme aufgelöst, um ${\displaystyle y_{(k)}}$ freistellen zu können: ${\displaystyle y_{(k)}{\bigg (}{\frac {0{,}25}{T_{\mathrm {A} }^{2}}}+{\frac {0{,}125}{T_{\mathrm {A} }}}+1{\bigg )}=u_{(k)}+{\frac {0{,}5y_{(k-1)}}{T_{\mathrm {A} }^{2}}}-{\frac {0{,}25y_{(k-2)}}{T_{\mathrm {A} }^{2}}}+{\frac {0{,}125y_{(k-1)}}{T_{\mathrm {A} }}}.}$ ${\displaystyle y_{(k)}={\frac {u_{(k)}}{\lambda }}+{\frac {0{,}5y_{(k-1)}}{\lambda T_{\mathrm {A} }^{2}}}-{\frac {0{,}25y_{(k-2)}}{\lambda T_{\mathrm {A} }^{2}}}+{\frac {0{,}125y_{(k-1)}}{\lambda T_{\mathrm {A} }}}\quad {\bigg |}\qquad \lambda ={\frac {0{,}25}{T_{\mathrm {A} }^{2}}}+{\frac {0{,}125}{T_{\mathrm {A} }}}+1}$ Berechnungsbeispiel für einige Werte der Ausgangsfolge ${\displaystyle y_{(k)}}$ mit ${\displaystyle T_{\mathrm {A} }=0{,}01;\quad \lambda =2513{,}5;\quad u_{(k)}=1}$: ${\displaystyle y_{(k=0)}=0{,}0004+0-0+0=0{,}0004}$. ${\displaystyle y_{(k=1)}=0{,}0004+0{,}0008-0+0=0{,}0012}$. ${\displaystyle y_{(k=2)}=0{,}0004+0{,}0024-0{,}0004+0=0{,}0024}$. ${\displaystyle y_{(k=157)}=0{,}0004+3{,}286-1{,}643+0{,}008=1{,}652}$.

Diese Differenzengleichung entspricht einem Rekursionsalgorithmus eines dynamischen Systems, der schrittweise mit einem digitalen Rechner gelöst werden kann.

Die rekursive Berechnung der Differenzengleichung 2. Ordnung bezieht sich für die aktuelle Ausgangsfolge ${\displaystyle y_{(k)}}$ durch Einsetzen der zurückliegenden Werte der Ausgangsfolge ${\displaystyle u_{(k-1)}}$ und ${\displaystyle u_{(k-2)}}$ in die Gleichung. Für das 1. Folgeglied der Berechnungsfolge k=0 sind die zurückliegenden Werte der Ausgangsfolge noch nicht verfügbar und damit Null. Die Anzahl ${\displaystyle k=(0,1,2,3,\dots ,k_{\text{max}})}$ der Glieder der Ausgangsfolge wird durch die diskrete Zeit ${\displaystyle T_{\mathrm {A} }}$ und durch die gewünschte zu beobachtende Gesamtzeit des Einschwingvorgangs bestimmt.

Anwendung zeitdiskreter Signale und dynamischer Systeme

Die z-Transformation wird auf zeitdiskrete Signale ${\displaystyle u_{(k)}}$, auf die systembeschreibenden Differenzengleichungen ${\displaystyle y_{(k)}}$ und auf Übertragungsfunktionen des s- und z-Bereiches meist mit Hilfe der Korrespondenztabellen angewendet.

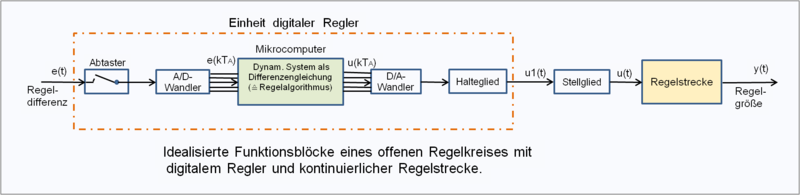
Das nebenstehende Bild ist ein Beispiel der Darstellung der Signalarten und Systeme an einem aufgeschnittenen digitalen Regelkreis mit einer kontinuierlichen Regelstrecke.

Abtastsysteme wandeln in Verbindung mit A/D-Wandlern ein kontinuierliches Signal in ein zeitdiskretes Signal als Wertefolge um. D/A-Wandler in Verbindung mit Haltesystemen nullter Ordnung wandeln eine Wertefolge in ein gestuftes zeitkontinuierliches Signal um.

z-Transformation einer Wertefolge (Impulsfolge)

Eine Wertefolge besteht aus ${\displaystyle k_{\mathrm {max} }}$ oder ${\displaystyle k=\infty }$ vielen Folgegliedern. Das Objekt mit der Nummer i wird i-tes Folgeglied oder i-te Komponente der Folge genannt. Die abgetasteten und digitalisierten Signale entsprechen einer Folge von modulierten impulsförmigen Signalen ${\displaystyle u(kT_{\mathrm {A} })}$ im Abstand ${\displaystyle T_{\mathrm {A} }}$, die erst nach der A/D-Wandlung mit einer Haltestufe zu einem gestuften quasi kontinuierlichem Signal ${\displaystyle u(t)}$ werden.

Die Laplace-Transformation bezieht sich auf die Ableitungen einer gewöhnlichen Differentialgleichung und ersetzt diese nach dem Laplace-Differentiationssatz durch die komplexe Variable ${\displaystyle s=\sigma +\mathrm {j} \omega }$. Ein Exponent von s kennzeichnet die Ordnung der Ableitung.

Die z-Transformation transformiert eine Impulsfolgefunktion ${\displaystyle f^{*}(t)}$ oder eine Zahlenfolge ${\displaystyle f_{(k)}}$ in eine Funktion ${\displaystyle F(z)}$ mit der z-Variable ${\displaystyle z=\mathrm {e} ^{T_{\mathrm {A} }\cdot s}}$.

Da die Berechnungen mit Impulsfunktionen oder Folgen aufwendig sind, ist es sinnvoll, diese durch einfachere Berechnungen im z-Bildbereich auszuführen. Die z-Transformation von Impulsfolgen kann als diskrete Laplace-Transformation aufgefasst werden.^{[Einzelnachweise 6]}

Die zu diskreten Zeitpunkten abgetasteten kontinuierlichen Eingangssignale entsprechen mit der Eingangsgröße modulierten (gewichteten) ${\displaystyle \delta }$-Impulsfolgen, die mit der z-Transformation berechnet werden.

Beim Übergang von kontinuierlichen Systemen f(t) zu Abtastsystemen ${\displaystyle f_{(k)}}$ mit der Abtastfolge ${\displaystyle k=(0,1,2,3,\dots )}$ gehen lineare zeitinvariante Differenzialgleichungen in zeitinvariante Differenzengleichungen der Abtastzeit T_A beziehungsweise der Abtastfrequenz ${\displaystyle f_{TA}=1/T_{\mathrm {A} }}$ der Funktion ${\displaystyle f(kT_{\mathrm {A} })}$ über.

Kontinuierliche Signale z. B. die Regelabweichung ${\displaystyle e(t)}$ eines Regelkreises mit einer analog arbeitenden Regelstrecke werden zu gleichen Zeitabständen ${\displaystyle T_{\mathrm {A} }}$ abgetastet. Ein Abtaster mit A/D-Wandler erzeugt aus einem zeitkontinuierlichen Regler-Eingangssignal ${\displaystyle e(t)}$ ein zeitdiskretes Signal ${\displaystyle e_{(k)}}$. Es können sowohl abgetastete Regler-Eingangssignale ${\displaystyle e_{(k)}}$ als auch Differenzengleichungen ${\displaystyle f(k)}$, die im diskreten Zeitbereich den Regelalgorithmus eines Reglers beschreiben, als z-Übertragungsfunktionen in den z-Bereich transformiert und als algebraische Gleichungen behandelt werden.

Wird eine inverse z-Transformation der z-Übertragungsfunktionen durchgeführt, entsteht die Lösung der zeitdiskreten Differenzengleichung ${\displaystyle f_{(k)}={\mathcal {Z}}^{-1}\{F(z)\}}$ im ${\displaystyle f(k)}$-Bereich. Mit Hilfe verschiedener Verfahren der Rücktransformation vom z-Bereich in den k-Bereich ergeben sich dann als Lösung die Differenzengleichungen des Regelalgorithmus für den diskreten Bereich ${\displaystyle f(k)}$.

Für die häufig vorkommenden Transformationen des k- und z-Bereiches stehen in vielen Fachbüchern der Regelungstechnik Transformationstafeln zur Verfügung.

Eine einzelne Abtastung eines kontinuierlichen Signals ${\displaystyle u(t)}$ an einer beliebigen Stelle des Signalverlaufs z. B. zum Zeitpunkt ${\displaystyle T_{1}}$ wird als Modulation von ${\displaystyle u(t)}$ mit einem Dirac-Impuls mit ${\displaystyle \delta \cdot (t-T_{1})}$ beschrieben.^{[Einzelnachweise 7][Einzelnachweise 8]}

Damit ergibt sich für die Multiplikation des Eingangssignals ${\displaystyle u(t)}$ mit dem Dirac-Impuls:

${\displaystyle u_{T_{1}}(t)=u(t)\cdot \delta (t-T1)=u(T_{1})\cdot \delta (t-T_{1}).}$

Wird nun periodisch mit zu den Zeitpunkten ${\displaystyle kT_{\mathrm {A} }}$ das Signal ${\displaystyle u(t)}$ abgetastet, kann das abgetastete Signal ${\displaystyle u(kT_{\mathrm {A} })=u_{k}}$ als Multiplikation einer ${\displaystyle \delta }$-Impulsfolge mit ${\displaystyle u(t)}$ betrachtet werden.

Die Impulsfolgefunktion bezieht sich auf die Summengrenzen von ${\displaystyle k=-\infty }$ zu ${\displaystyle k=\infty :}$

${\displaystyle u(t)=\sum _{k=-\infty }^{\infty }u(kT_{\mathrm {A} })\cdot \delta (t-kT_{\mathrm {A} }).}$

Mit dem Übergang der Summengrenzen von ${\displaystyle k=0}$ zu ${\displaystyle k=\infty }$ wird die Impulsfolgefunktion:

${\displaystyle u(t)=\left.\sum _{k=0}^{\infty }u_{k}\cdot \delta (t-kT_{\mathrm {A} })\right|_{{\text{mit }}u_{k}=0{\text{ für }}k<0}.}$

Die Impulsfolgefunktion wird der Laplace-Transformation unterzogen:

${\displaystyle U(s)={\mathcal {L}}{\Bigl \{}\sum _{k=0}^{\infty }u_{k}\cdot \delta (t-kT_{\mathrm {A} }){\Bigr \}}=\int \limits _{0}^{\infty }\sum _{k=0}^{\infty }u_{k}\cdot \delta (t-kT_{\mathrm {A} })\cdot \mathrm {e} ^{-st}\mathrm {d} t=\sum _{k=0}^{\infty }u_{k}\cdot \mathrm {e} ^{-k\cdot s\cdot T_{\mathrm {A} }}.}$

Mit der z-Variablen ${\displaystyle z=\mathrm {e} ^{s\cdot T_{\mathrm {A} }}}$ und ${\displaystyle z^{-k}=\mathrm {e} ^{-ksT_{\mathrm {A} }}}$ wird die Gleichung vereinfacht zu der z-Transformierten des kontinuierlichen Signals ${\displaystyle u(t)}$.

Mit ${\displaystyle z=\mathrm {e} ^{s\cdot T_{\mathrm {A} }}}$ wird die s-Ebene auf die z-Ebene abgebildet.

Damit lautet die z-Transformation eines abgetasteten kontinuierlichen Signals ${\displaystyle u(t)}$ mit der Folge ${\displaystyle k=(0,1,2,3,\dots )}$ und der Wertefolge ${\displaystyle u(kT_{\mathrm {A} }):=u_{k}=[u_{(0)};u_{(T_{\mathrm {A} })};u_{(2T_{\mathrm {A} })};u_{(3T_{\mathrm {A} })};\cdots ]}$:

${\displaystyle {\mathcal {Z}}\{u_{(k)}\}=U(z)=\sum _{k=0}^{\infty }u_{k}\cdot z^{-k}}$

oder allgemein als Funktion ${\displaystyle F(z)}$:

${\displaystyle F(z)=\sum _{k=0}^{\infty }f_{k}\cdot z^{-k}}$

Rechenregeln der z-Transformation

Wie die Laplace-Transformation wird die z-Transformation durch Sätze und Rechenregeln definiert, dennoch bestehen in einigen Funktionen große Unterschiede.

Die Transformationen und Rücktransformationen der z-Transformation erfolgen meist mit Hilfe von Transformations-Tabellen. In der Fachliteratur werden in Tabellen die Zeitfunktionen ${\displaystyle f(t)}$, die Laplace-Transformierten ${\displaystyle f(s)}$ und die z-Transformierten ${\displaystyle f(z)}$ dargestellt. Nicht vorhandene Zeitfunktionen für die inverse z-Transformation können wie bei der Laplace-Transformation durch die Partialbruchzerlegung bestimmt werden.

Die Verfahren der Anwendung der Rechenregeln der z-Transformationen sind umfangreich und können in diesem Abschnitt nur angedeutet werden. Die nachstehenden meist tabellarisch aufgeführten Verfahren sind in jedem guten Fachbuch der Regelungstechnik oder in Vorlesungsmanuskripten der z-Transformation zu finden.

• Diese Rechenregeln beziehen sich auf Linearitätssätze, Multiplikationssatz, Divisionssatz, Ähnlichkeitssätze, Dämpfungssatz, Verschiebungssätze (rechts-links), Differenzensätze (Rückwärts-Vorwärts), Summationssatz, Faltungssatz, Grenzwertsätze.
• Die z-Transformationen und die z-Rücktransformationen können mit Hilfe von Transformations-Tabellen und verschiedenen noch dargestellten Verfahren durchgeführt werden.

Die nachfolgenden mathematischen Beziehungen gelten für Systeme mit einem Eingangssignal ${\displaystyle u_{(k)}}$ und einem Ausgangssignal ${\displaystyle y_{(k)}}$. Für einen digitalen Regler müssen die zugehörigen Größen des Eingangssignals ${\displaystyle e_{(k)}}$ und Ausgangssignals ${\displaystyle u_{(k)}}$ in die Gleichungen eingesetzt werden.

Die wichtigsten Eigenschaften der z-Transformation:^{[Einzelnachweise 9]}

• Grundlagen der Definitionen im z-Bereich:

z-Variable:

${\displaystyle z=\mathrm {e} ^{T_{\mathrm {A} }\cdot s}}$

z-Transformierte einer Folge ${\displaystyle f_{(k)}}$:

${\displaystyle F(z)={\mathcal {Z}}\{f_{(k)}\}}$

Inverse z-Transformation von F(z):

${\displaystyle f_{(k)}={\mathcal {Z}}^{-1}\{F(z)\}}$

• Für Grenzbetrachtungen treten häufig folgende Fälle auf:

Für den s-Bildbereich gilt für die s-Variable.

${\displaystyle \lim _{t\to +0}f(t)=\lim _{s\to \infty }s\cdot F(s)}$

${\displaystyle \lim _{t\to \infty }f(t)=\lim _{s\to 0}s\cdot F(s)}$

Für den z-Bildbereich gilt für die z-Variable:

${\displaystyle f(k=0)=\lim _{z\to \infty }F(z)}$

${\displaystyle \lim _{k\to \infty }f(k)=\lim _{z\to 1}(z-1)\cdot F(z)}$

• Anfangswert einer zeitdiskreten Folge:

${\displaystyle u(k=0)=\lim _{z\to \infty }U(z)}$

• Rückwärtsverschiebung (nach rechts):

Totzeiten innerhalb eines Digitalreglers entstehen durch die Signalabtastung über A/D-Wandler, D/A-Wandler und durch die Rechenzeit des Mikrocomputers. Die Berechnung einer Totzeit ${\displaystyle T_{t}=d\cdot T_{\mathrm {A} }}$ einer Abtastfolge entspricht einer Rückwärtsverschiebung (Rechtsverschiebung) der Abtastfolge (Zahlenwerte) um d Abtastschritte von ${\displaystyle T_{\mathrm {A} }}$. Diese mathematische Operation bedeutet im s-Bereich für die Totzeit ${\displaystyle \mathrm {e} ^{-s\cdot T_{t}}}$ und im z-Bereich:

${\displaystyle u_{(k-d)}\ \circ \!\!-\!\!\bullet \ z^{-d}\cdot U(z)}$

• Vorwärtsverschiebung (nach links):

Eine Vorhersage um die Zeit ${\displaystyle T_{P}=d\cdot T_{\mathrm {A} }}$ einer Wertefolge entspricht einer Vorwärtsverschiebung nach links um d-Abtastschritte. Diese Operation entspricht der Laplace-Transformierten ${\displaystyle \mathrm {e} ^{s\cdot T_{\mathrm {A} }}}$ und bedeutet im z-Bereich:

${\displaystyle u_{(k+d)}\ \circ \!\!-\!\!\bullet \ z^{d}\cdot U(z)}$

• Differentiation:

Die Differenz zweier aufeinander folgender Abtastwerte dividiert durch die Abtastzeit entspricht der Annäherung an einen Differenzialquotienten im Zeitbereich.

${\displaystyle u_{(k)}-u_{(k-1)}\ \circ \!\!-\!\!\bullet \ {\frac {z-1}{z}}\cdot U(z)}$

• Integration:

Wird die Summe aller Abtastwerte mit der Abtastzeit T_A multipliziert, entsteht in Annäherung an den Zeitbereich die numerische Integration. Im s-Bereich entspricht die Integration 1 / s. Im z-Bereich gilt für die Integration:

${\displaystyle \sum _{i=0}^{k}u_{(i)}\ \circ \!\!-\!\!\bullet \ {\frac {z}{z-1}}\cdot U(z)}$

• Gewichtsfolge:

Die z-Übertragungsfunktion G(z) ist die z-Transformierte der Gewichtsfolge g(k).

${\displaystyle G(z)\ \bullet \!\!-\!\!\circ \ g(k)}$

In G(z) und g(k) sind alle Eigenschaften eines linearen, zeitdiskreten dynamischen Systems enthalten.

• Multiplikation:

Ausgangssignal als Funktion des Eingangssignals und der z-Übertragungsfunktion

${\displaystyle Y(z)=U(z)\cdot G(z)}$

• Faltung der Impulsfolgen:

${\displaystyle y_{(k)}=\sum _{i=0}^{k}g_{(i)}\cdot u_{(k-i)}}$

Im Bildbereich steht die Multiplikation an Stelle der Faltungssumme, wie bei zeitkontinuierlichen Systemen an Stelle des Faltungsintegrals.

Tabelle der Korrespondenzen des Zeitbereichs f(t), des Laplace- und z-Bereichs (Auszüge)

^{[Einzelnachweise 10]}

Funktion im Zeitbereich f(t)	Laplace-Transformierte im Bildbereich F(s)	Diskrete Laplace-Transformierte nach der z-Transformation ${\displaystyle F(z)={\mathcal {Z}}\{F(s)\}}$
δ-Impuls	1	1
Einheits- sprung 1	${\displaystyle {\frac {1}{s}}}$	${\displaystyle {\frac {z}{z-1}}}$
t	${\displaystyle {\frac {1}{s^{2}}}}$	${\displaystyle {\frac {T_{\mathrm {A} }\cdot z}{(z-1)^{2}}}}$
${\displaystyle t^{2}}$	${\displaystyle {\frac {2}{s^{3}}}}$	${\displaystyle {\frac {T_{\mathrm {A} }^{2}\cdot z\cdot (z+1)}{(z-1)^{3}}}}$
${\displaystyle \mathrm {e} ^{-a\cdot t}}$	${\displaystyle {\frac {1}{s+a}}}$	${\displaystyle {\frac {z}{z-\mathrm {e} ^{-a\cdot T_{\mathrm {A} }}}}}$
${\displaystyle t\cdot \mathrm {e} ^{-a\cdot t}}$	${\displaystyle {\frac {1}{(s+a)^{2}}}}$	${\displaystyle {\frac {\mathrm {e} ^{-a\cdot T_{\mathrm {A} }}\cdot T_{\mathrm {A} }\cdot z}{(z-\mathrm {e} ^{-a\cdot T_{\mathrm {A} }})^{2}}}}$
${\displaystyle 1-\mathrm {e} ^{-a\cdot t}}$	${\displaystyle {\frac {a}{s\cdot (s+a)}}}$	${\displaystyle {\frac {(1-\mathrm {e} ^{-a\cdot T_{\mathrm {A} }})\cdot z}{(z-1)\cdot (z-\mathrm {e} ^{-a\cdot T_{\mathrm {A} }})}}}$
${\displaystyle 1-\mathrm {e} ^{-t/T_{1}}}$	${\displaystyle {\frac {1}{s\cdot (1+T_{1}\cdot s)}}}$	${\displaystyle {\frac {(1-\mathrm {e} ^{-T_{\mathrm {A} }/T_{1}})\cdot z}{(z-1)\cdot (z-\mathrm {e} ^{-T_{\mathrm {A} }/T_{1}})}}}$
${\displaystyle \sin \omega _{0}t}$	${\displaystyle {\frac {\omega _{0}}{s^{2}+\omega _{0}^{2}}}}$	${\displaystyle {\frac {z\cdot \sin(\omega _{0}T_{\mathrm {A} })}{z^{2}-2z\cdot \cos(\omega _{0}T_{\mathrm {A} })+1}}}$
${\displaystyle \cos \omega _{0}t}$	${\displaystyle {\frac {s}{s^{2}+\omega _{0}^{2}}}}$	${\displaystyle {\frac {z^{2}-z\cdot \cos(\omega _{0}T_{\mathrm {A} })}{z^{2}-2z\cdot \cos(\omega _{0}T_{\mathrm {A} })+1}}}$
${\displaystyle 1-(1+at)\mathrm {e} ^{-at}}$	${\displaystyle {\frac {a^{2}}{s\cdot (s+a)^{2}}}}$	${\displaystyle {\frac {z}{z-1}}-{\frac {z}{z-c}}-{\frac {acT_{\mathrm {A} }z}{(z-c)^{2}}}\ ;\quad c=\mathrm {e} ^{-aT_{\mathrm {A} }}}$
${\displaystyle 1+{\frac {b\mathrm {e} ^{-at}-a\mathrm {e} ^{-bt}}{a-b}}}$	${\displaystyle {\frac {ab}{s\cdot (s+a)(s+b)}}}$	${\displaystyle {\frac {z}{z-1}}+{\frac {bz}{(a-b)(z-c)}}-{\frac {az}{(a-b)(z-d)}}}$ ${\displaystyle c=\mathrm {e} ^{-aT_{\mathrm {A} }}\ \quad d=\mathrm {e} ^{-bT_{\mathrm {A} }}}$
${\displaystyle \mathrm {e} ^{-at}\sin \omega _{0}t}$	${\displaystyle {\frac {\omega _{0}}{(s+a)^{2}+\omega _{0}^{2}}}}$	${\displaystyle {\frac {cz\sin(\omega _{0}T_{\mathrm {A} })}{z^{2}-2cz\cos(\omega _{0}T_{\mathrm {A} })+c^{2}}}\ ;\quad c=\mathrm {e} ^{-aT_{\mathrm {A} }}}$
${\displaystyle \mathrm {e} ^{-at}\cos \omega _{0}t}$	${\displaystyle {\frac {s+a}{(s+a)^{2}+\omega _{0}^{2}}}}$	${\displaystyle {\frac {z^{2}-cz\cos(\omega _{0}T_{\mathrm {A} })}{z^{2}-2cz\cos(\omega _{0}T_{\mathrm {A} })+c^{2}}}\ ;\quad c=\mathrm {e} ^{-aT_{\mathrm {A} }}}$
${\displaystyle a^{t/T_{\mathrm {A} }}}$	${\displaystyle {\frac {1}{s-(1/T_{\mathrm {A} })\ln a}}}$	${\displaystyle {\frac {z}{z-a}}}$${\displaystyle }$

T_A = Abtastzeit, a oder b = Zahlenwert der Nullstelle (Pol) im s-Bereich, T₁ = Zeitkonstante der s-Übertragungsfunktion.

Tabelle der Korrespondenzen der zeitdiskreten Funktionen f_(k) zum z-Bereich F(z) (Auszüge)

Name der Zeitfunktion	Wertefolge ${\displaystyle f_{(k)}}$	z-Transformierte
${\displaystyle \delta }$-Impulsfolge	${\displaystyle f_{(k)}=[0(-T_{\mathrm {A} }),1(0T_{\mathrm {A} }),0(T_{\mathrm {A} }),0(2T_{\mathrm {A} }),0(3T_{\mathrm {A} }),\dots ]}$	1
Sprungfolge	${\displaystyle f_{(k)}=[0(-T_{\mathrm {A} }),1(0T_{\mathrm {A} }),1(T_{\mathrm {A} }),1(2T_{\mathrm {A} }),1(3T_{\mathrm {A} }),\dots ]}$	${\displaystyle {\frac {z}{z-1}}}$
Anstiegsfolge	${\displaystyle u_{(k)}=[-u_{1}(-T_{\mathrm {A} }),u_{0}(0T_{\mathrm {A} }),u_{1}(T_{\mathrm {A} }),u_{2}(2T_{\mathrm {A} }),u_{3}(3T_{\mathrm {A} }),\dots ]}$ ${\displaystyle k=[-1,0,1,2,3,\dots ]}$	${\displaystyle {\frac {z}{(z-1)^{2}}}}$
Potenzfolge	${\displaystyle a^{k}}$	${\displaystyle {\frac {z}{z-a}}}$
e-Funktionsfolge	${\displaystyle \mathrm {e} ^{-ak}}$	${\displaystyle {\frac {z}{z-\mathrm {e} ^{-a}}}}$
Sinusfunktionsfolge	${\displaystyle \sin(ak)}$	${\displaystyle {\frac {z\cdot \sin a}{z^{2}-2z\cdot \cos a+1}}}$
Kosinusfunktionsfolge	${\displaystyle \cos(ak)}$	${\displaystyle {\frac {z\cdot (z-\cos a)}{z^{2}-2z\cdot \cos a+1}}}$
Abklingende Sinus- funktionsfolge	${\displaystyle \mathrm {e} ^{-ak}\cdot \sin(bk)}$	${\displaystyle {\frac {z\cdot \mathrm {e} ^{-a}\cdot \sin b}{z^{2}-2z\cdot \mathrm {e} ^{-a}\cdot \cos \ b+\mathrm {e} ^{-2a}}}}$
Abklingende Cosinus- funktionsfolge	${\displaystyle \mathrm {e} ^{-ak}\cdot \cos(bk)}$	${\displaystyle {\frac {z\cdot (z-\mathrm {e} ^{-a}\cdot \cos b)}{z^{2}-2z\cdot \mathrm {e} ^{-a}\cdot \cos \ b+\mathrm {e} ^{-2a}}}}$
Linearitätssatz	${\displaystyle a_{1}f_{1}(k)+a_{2}f_{2}(k)+\dots +a_{n}f_{n}(k)}$	${\displaystyle a_{1}F_{1}(z)+a_{2}F_{2}(z)+\dots +a_{n}F_{n}(z)}$
Rechts-Verschiebesatz	${\displaystyle f(k-d)}$	${\displaystyle z^{-d}\cdot F(z)}$
Faltungssumme	${\displaystyle \sum _{i=0}^{k}f_{1}(i)\cdot f_{2}(k-i)}$	${\displaystyle F_{1}(z)\cdot F_{2}(z)}$
Anfangswertsatz	${\displaystyle \lim _{k\to 0}f(k)}$	${\displaystyle \lim _{z\to \infty }F(z)}$
Endwertsatz	${\displaystyle \lim _{k\to \infty }f(k)}$	${\displaystyle \lim _{z\to 1}\,(z-1)\cdot F(z)}$

Z-Übertragungsfunktion (Impulsübertragungsfunktion) von zeitdiskreten Elementen

Übersicht:

• Die Differenzengleichungen ${\displaystyle y_{(k)}}$ können ausschließlich mit Hilfe des Linearitätssatzes und Verschiebungssatzes in den komplexen z-Bildbereich und in die z-Übertragungsfunktionen ${\displaystyle G(z)=Y(z)/U(z)}$ überführt werden.

Wendet man auf die einzelnen Terme der Differenzengleichung den Linearitäts- und den rechts-Verschiebungssatz an und bringt alle Terme mit ${\displaystyle y_{(k)}}$ auf die linke Seite und alle Terme mit ${\displaystyle u_{(k)}}$ auf die rechte Seite der Differenzengleichung, so lässt sich das Verhältnis ${\displaystyle G(z)=Y(z)/U(z)}$ mit den verbleibenden Elementen als gebrochen-rationale Funktion darstellen.

Die z-Übertragungsfunktion lautet:

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {{\text{Zählerpolynom}}\ (z)}{{\text{Nennerpolynom}}\ (z)}}}$

• Gegebene Übertragungsfunktionen des s-Bereiches in Verbindung mit Haltegliedern und Abtastelementen können ebenfalls mit Hilfe der Korrespondenztabellen als z-Übertragungsfunktion transformiert werden.
• Die Rücktransformation von der z-Übertragungsfunktion in den zeitdiskreten Bereich als Differenzengleichung erfolgt durch den invers angewendeten Linearitätssatz und Verschiebungssatz für alle einzelnen Terme. Durch die kreuzweise Multiplikation von ${\displaystyle y_{(k)}}$ und ${\displaystyle u_{(k)}}$ mit den Polynomen im Zähler und Nenner der z-Übertragungsfunktion entsteht wieder eine Differenzengleichung ${\displaystyle y_{(k)}}$, wenn die einzelnen Terme der inversen Transformation unterzogen werden.

Mit der so errechneten Differenzengleichung des Übertragungssystems ist man nun in der Lage, für eine gegebene Eingangserregung ${\displaystyle u_{(k)}}$ des Systems die Ausgangsfolgen des Systems ${\displaystyle y_{(k)}}$ zu berechnen. Dies ist auf verschiedenen Arten möglich.

• Analytische Berechnung mit Hilfe der Korrespondenztabellen der z-Transformation,
• Rekursive Berechnung von Systemantworten der Differenzengleichungen mit Bezug auf zurückliegende Folgen k.

Entstehung der z-Übertragungsfunktion:

Ein zeitdiskretes dynamisches System wird durch eine rekursive Differenzengleichung beschrieben.

Wie bei zeitkontinuierlichen Systemen ${\displaystyle g(t)}$ und der Übertragungsfunktion ${\displaystyle G(s)}$ besteht eine vergleichbare Beziehung bei den zeitdiskreten Systemen zwischen der Gewichtsfolge ${\displaystyle g(k)}$ und z-Übertragungsfunktion G(z). Die Übertragungsfunktion ${\displaystyle G(z)}$ ist die z-Transformierte der Gewichtsfolge ${\displaystyle g(k)}$.

${\displaystyle G(z)\ \bullet \!\!-\!\!\circ \ g(k)}$

In G(z) und g(k) sind alle Eigenschaften eines dynamischen Systems enthalten. Zur Systemberechnung wird der Verlauf des Eingangssignals U(z) und das Systemverhalten G(z) oder g(k) benötigt.

Für die Ermittlung der z-Übertragungsfunktion ist die Gewichtsfunktion g(t) die Systemantwort (Impulsantwort) auf die Vorgabe eines Eingangs-DIRAC-Impulses ${\displaystyle \delta }$(t).

Bei der Laplace-Transformation eines Systems lautet die Übertragungsfunktion:

${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {{\text{Zählerpolynom}}\ (s)}{{\text{Nennerpolynom}}\ (s)}}\ |\qquad {\text{mit }}U(s)=\delta (t)}$

Aus der Gewichtsfunktion wird die Impulsfolgefunktion ${\displaystyle g^{*}(t)}$ oder die Gewichtsfolge g(kT_A) gebildet und in den z-Bereich transformiert. Die z-Übertragungsfunktion von zeitkontinuierlichen Systemen ergibt sich mit folgender Vorschrift:

${\displaystyle G(z)={\mathcal {Z}}\{g(t)|_{t=kT_{\mathrm {A} }}\}={\mathcal {Z}}\{{\mathcal {L}}^{-1}\{G(s)\}|_{t=kT_{\mathrm {A} }}\}}$

Die Berechnung der Impulsübertragung von linearen zeitdiskreten Systemen vereinfacht sich, wenn aus der Differenzengleichung mit der z-Transformation die z-Übertragungsfunktion bestimmt wird. So können z. B. die Regelalgorithmen eines digitalen Reglers mit Differenzengleichungen formuliert werden.^{[Einzelnachweise 11][Einzelnachweise 12]}

Ist die z-Übertragungsfunktion eines Systems G(z) gegeben, lässt sich die zugehörige z-Differenzengleichung bestimmen:

• durch Ausmultiplizieren von Zähler und Nenner ${\displaystyle y(z)}$ und ${\displaystyle u(z)}$ und Gleichungsumstellung nach ${\displaystyle y(z)}$,
• Anwendung des rechts-Verschiebesatzes der z-Transformation zur Bestimmung der Ausgangsgröße ${\displaystyle y_{(k)}}$.

Es wird eine lineare Differenzengleichung eines Regelalgorithmus gegeben:

Die Eingangssignale der Differenzengleichung sind wieder ${\displaystyle u_{(k)}}$ und die Ausgangssignale ${\displaystyle y_{(k)}}$.

${\displaystyle a_{n}\cdot y_{(k+n)}+a_{n-1}\cdot y_{(k+n-1)}+\cdots +a_{1}\cdot y_{(k+1)}+a_{0}\cdot y_{(k)}=b_{m}\cdot u_{(k+m)}+b_{m-1}\cdot u_{(k+m-1)}+\cdots +b_{1}\cdot u_{(k+1)}+b_{0}\cdot u_{(k)}|\qquad n\geq m}$

Unter der Voraussetzung, dass die Anfangswerte des zeitdiskreten Systems gleich Null sind, wird die Differenzengleichung transformiert. Mit den Rechenregeln des rechts-Verschiebungssatzes ergibt sich die Transformationsvorschrift:

${\displaystyle y_{(k)}\to y(z),\qquad y_{(k+i)}\to z^{i}\cdot y(z),\qquad y_{(k-i)}\to z^{-i}\cdot y(z)}$,

${\displaystyle u_{(k)}\to u(z),\qquad u_{(k+i)}\to z^{i}\cdot u(z),\qquad u_{(k-i)}\to z^{-i}\cdot u(z)}$

Die z-transformierte Differenzengleichung ergibt sich zu:

${\displaystyle a_{n}\cdot z^{n}\cdot Y(z)+a_{n-1}\cdot z^{n-1}\cdot Y(z)+\cdots +a_{1}\cdot z\cdot Y(z)+a_{0}\cdot Y(z)=b_{m}\cdot z^{m}\cdot U(z)+b_{m-1}\cdot z^{m-1}\cdot U(z)+\cdots +b_{1}\cdot z\cdot U(z)+b_{0}\cdot U(z)}$

Durch Ausklammern des Quotienten Y(z) / U(z) kann die Impulsübertragungsfunktion G(z) gebildet werden.

Damit lautet die z-Übertragungsfunktion:

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {b_{m}\cdot z^{m}+b_{m-1}\cdot z^{m-1}+\cdots +b_{1}\cdot z+b_{0}}{a_{n}\cdot z^{n}+a_{n-1}\cdot z^{n-1}+\cdots +a_{1}\cdot z+a_{0}}}={\frac {{\text{Zähler}}(z)}{{\text{Nenner}}(z)}}}$

Bei der Berechnung von Differenzengleichungen mit dem Digitalrechner ist die von n-Schritten nach rechts verschobene Gleichung besser geeignet.

${\displaystyle a_{n}\cdot y_{(k)}+a_{n-1}\cdot y_{(k-1)}+\cdots +a_{1}\cdot y_{(k-n+1)}+a_{0}\cdot y_{(k-n)}=b_{m}\cdot u_{(k-n+m)}+b_{m-1}\cdot u_{(k-n+m-1)}+\cdots +b_{1}\cdot u_{(k-n+1)}+b_{0}\cdot u_{(k-n)}}$

Damit lautet die z-Übertragungsfunktion mit negativen Exponenten von z:

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {b_{m}\cdot z^{m-n}+b_{m-1}\cdot z^{m-1-n}+\cdots +b_{1}\cdot z^{-n+1}+b_{0}\cdot z^{-n}}{a_{n}+a_{n-1}\cdot z^{-1}+\cdots +a_{1}\cdot z^{-n+1}+a_{0}\cdot z^{-n}}}}$

Beispiel: Für eine gegebenen Differenzengleichung 3. Ordnung lautet die z-Übertragungsfunktion für Ordnungen m = 2 und n = 3:

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {b_{2}\cdot z^{2}+b_{1}\cdot z+b_{0}}{a_{3}\cdot z^{3}+a_{2}\cdot z^{2}+a_{1}\cdot z+a_{0}}}}$

Mit der rechts-Verschiebung der zugehörigen Differenzengleichung um n = 3 Abtastschritte ${\displaystyle T_{\mathrm {A} }}$ lautet die z-Übertragungsfunktion:

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {b_{2}\cdot z^{-1}+b_{1}\cdot z^{-2}+b_{0}\cdot z^{-3}}{a_{3}+a_{2}\cdot z^{-1}+a_{1}\cdot z^{-2}+a_{0}\cdot z^{-3}}}}$

Es fällt auf, dass die z-Transformation einer Differenzengleichung eine große Ähnlichkeit mit der Polynomform einer s-Übertragungsfunktion für kontinuierliche Systeme hat. Ebenso fällt auf, dass die z-Übertragungsfunktion negative Potenzen hat. Allgemein werden z-Übertragungsfunktionen mit negativen Potenzen von z dargestellt.

Jede z-Übertragungsfunktion mit negativen Potenzen von z kann in eine Form mit positiven Potenzen von z gebracht werden, wenn Zähler und Nenner der z-Übertragungsfunktion mit der höchsten vorkommenden inversen z-Potenz multipliziert werden. Für die z-Übertragungsfunktion der Form mit positiven Exponenten muss gelten: Grad des Nennerpolynoms ≥ Grad des Zählerpolynoms. Ist diese Bedingung erfüllt, ist G(z) kausal.

Es können sowohl abgetastete Eingangssignale u(kT_A) als auch Differenzengleichungen f(kT_A), die im diskreten Zeitbereich das Verhalten eines Systems (z. B. den Regelalgorithmus eines Reglers) beschreiben, als z-Übertragungsfunktionen in den z-Bereich transformiert und als algebraische Gleichungen behandelt werden.

Wird eine inverse z-Transformation der z-Übertragungsfunktionen durchgeführt, entsteht die Lösung der zeitdiskreten Differenzengleichung ${\displaystyle f_{(k)}={\mathcal {Z}}^{-1}\{F(z)\}}$ im ${\displaystyle f(kT_{\mathrm {A} })}$-Bereich. Mit Hilfe verschiedener Verfahren der Rücktransformation vom z-Bereich in den k-Bereich ergeben sich dann als Lösung die Differenzengleichungen des Regelalgorithmus für den diskreten Bereich f(kT_A).

Die typische Anwendung der z-Transformation eines digitalen Systems, eines digitalen Reglers oder eines digitalen Filters, für den Regelalgorithmus lautet wie folgt:

• Die Abtastfolge des Eingangssignals (Eingangsfolge) wird transformiert als z-Übertragungsfunktion ${\displaystyle H(z)}$,
• Die Differenzengleichung ${\displaystyle f_{(k\cdot T_{\mathrm {A} })}}$ des gewünschten Reglerverhaltens wird transformiert als z-Übertragungsfunktion ${\displaystyle G(z)}$,
• Die z-transformierten Systeme werden algebraisch entsprechend der z-Rechenregeln zusammengefasst,
• Mit der inversen z-Transformation des z-Produktes von Signal und Regelalgorithmus entsteht der Berechnungsalgorithmus des digitalen Reglers (Mikro Computers) wieder als Differenzengleichung.

Die Analyse und die Synthese diskreter Signale und Systeme lässt sich mit der z-Transformation erleichtern, setzt aber auch umfangreiches mathematisches Spezialwissen voraus.

Für die häufig vorkommenden Transformationen des k- und z-Bereich stehen in vielen Fachbüchern der Regelungstechnik Transformationstafeln zur Verfügung.

Z-Übertragungsfunktion einer Totzeit

Eine Totzeit T_t hat im Zeitbereich das Verhalten ${\displaystyle \displaystyle y(t)={u}(t-T_{t})}$.

Im s-Bereich lautet die Übertragungsfunktion eines Totzeitsystems:

${\displaystyle G(s)={\frac {y(s)}{u(s)}}=\mathrm {e} ^{-s\cdot T_{t}}}$

Es handelt sich hier bei der Verbindung einer s-Übertragungsfunktion als gebrochen-rationalen Funktion mit einem Totzeitglied um eine transzendente Funktion, die als Anhang einer Übertragungsfunktion – beispielsweise einer Regelstrecke – multiplikativ zugeordnet wird, mit der Einschränkung, dass keine algebraische Behandlung erlaubt ist.

Im z-Bereich entspricht eine Totzeit ${\displaystyle T_{t}=d\cdot T_{\mathrm {A} }}$ einer Rückwärtsverschiebung (Verschiebung nach rechts) der Abtastfolgen um d Abtastschritte. Die z-Übertragungsfunktion des Totzeitgliedes in Verbindung mit weiteren z-Übertragungssystemen bleibt gebrochen-rational (Bruch mit Zähler- und Nennerpolynom).

Für die z-Transformation der Abtastfolge für das Signal ${\displaystyle u_{(k-d)}}$ gilt:

${\displaystyle u_{(k-d)}\ \circ \!\!-\!\!\bullet \ z^{-d}\cdot U(z)}$

Anders als bei der Laplace-Transformation bedeutet ein Totzeitglied in Verbindung mit einer z-Übertragungsfunktion keine Einschränkung der bestehenden Form der gebrochen-rationalen Funktion. Eine z-Übertragungsfunktion mit einer mit ${\displaystyle d}$ Abtastschritten ${\displaystyle T_{\mathrm {A} }}$ definierten Totzeit ${\displaystyle T_{t}=d\cdot T_{\mathrm {A} }}$ wird durch Hinzufügen eines Terms ${\displaystyle z^{-d}}$ berücksichtigt. Es können beliebige algebraische Operationen durchgeführt werden.

Beispiel einer z-Übertragungsfunktion mit Totzeit:

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {b_{m}\cdot z^{m}+b_{m-1}\cdot z^{m-1}+\cdots +b_{1}\cdot z+b_{0}}{a_{n}\cdot z^{n}+a_{n-1}\cdot z^{n-1}+\cdots +a_{1}\cdot z+a_{0}}}\cdot z^{-d}}$

Z-Übertragungsfunktion von zeitkontinuierlichen Elementen G(s) mit Abtaster und Halteglied

Definition der Signale: Allgemein gilt für den Zeitbereich ${\displaystyle f(t)}$, zeitdiskreten Bereich ${\displaystyle f(k)}$ und Bildbereich ${\displaystyle f(s)}$, ${\displaystyle f(z)}$ die Eingangsgröße ${\displaystyle u}$ und die Ausgangsgröße ${\displaystyle y}$.

Abtastsysteme erlauben eine Umwandlung kontinuierlicher Signale in zeitdiskrete Abtastfolgen (Impulsfolgen). Halteglieder erlauben eine Umwandlung zeitdiskreter Ausgangsfolgen (Impulsfolgen) in kontinuierliche gestufte Signale im Zeitbereich. Ein Abtaster setzt ein kontinuierliches Signal ${\displaystyle u(t)}$ in Verbindung mit einem nachgeschalteten A/D-Wandler in eine Zahlenfolge ${\displaystyle u(k)}$ mit digitalen Werten um.

Ein Halteglied nullter Ordnung setzt eine Zahlenfolge ${\displaystyle u_{(k)}}$ mit einem vorgeschalteten D/A-Wandler in ein gestuftes kontinuierliches Signal ${\displaystyle u(t)}$ um. Bei der Reihenschaltung von einem Abtastsystem (gewichteter δ-Abtaster) und einem Halteglied handelt es sich um die Umwandlung einer aus einem kontinuierlichen Eingangssignal modulierten Impulsfolge in eine gestufte Treppenfunktion ${\displaystyle f(t)}$, die in ein kontinuierliches dynamisches System eingeleitet werden kann.

Liegt ein kontinuierliches dynamisches System vor, erlaubt die Abtastung eines kontinuierlichen Signals, z. B. eine Regelabweichung, die Verarbeitung einer zeitdiskreten Eingangsfolge in einem Mikrocomputer als Regelalgorithmus zu einer zeitdiskreten Ausgangsfolge. Die über ein Halteglied geleitete Ausgangsfolge erzeugt ein quasi stetiges gestuftes Ausgangssignal zu einer analogen zeitabhängigen Stellgröße.

Je nach Anwendung des kontinuierlichen Systems ${\displaystyle G(s)}$, beispielsweise in der Regelungstechnik, werden unterschiedlich Funktionsblöcke zusammengefasst, die auch mehrere Abtaster und Halteglieder enthalten können.

Um ein kontinuierliches System ${\displaystyle G(s)}$ in eine z-Übertragungsfunktion (Impulsübertragungsfunktion) zu definieren, muss es im Eingang durch eine Abtastfolge ${\displaystyle e_{(k)}}$ als Eingangsfolge und am Ausgang des Systems zeitsynchron durch einen Abtaster die Ausgangsfolge ${\displaystyle u_{(k)}}$ zur Verfügung stellen.

Je nachdem wie die Reihenfolge der Funktionsblöcke eines Haltegliedes ${\displaystyle G_{H}(s)}$, eines Systems ${\displaystyle G(s)}$ und eines Abtasters festgelegt sind, können diese Funktionsblöcke als ein Teil einer offenen Regelstrecke betrachtet werden. Die wären z. B.:

• Ein Haltegliedsystem mit analogem Ausgang, ein dynamisches System ${\displaystyle G(s)}$ und Abtastsystem für eine Ausgangsfolge,
• Ein Abtastsystem einer analogen Regelabweichung, Mikroprozessor für den Regelalgorithmus des Systems ${\displaystyle G(s)}$ und ein Haltegliedsystem für die Ausgabe eines kontinuierlichen Signals als Stellgröße für eine kontinuierliche Regelstrecke.

Das obere Grafikbild zeigt die Kombination der Funktionsblöcke Halteglied, kontinuierliches System ${\displaystyle G(s)}$ und Abtaster.

Damit ein kontinuierliches System ${\displaystyle G(s)}$ in eine (Impuls-)Übertragungsfunktion ${\displaystyle G(z)}$ definiert werden kann, muss das System durch eine Impulsfolge (Wertefolge) gespeist und am Ausgang ein Abtaster eingesetzt sein, der synchron zur Eingangsfolge eine Ausgangsfolge realisiert. Das Halteglied vor dem dynamischen System wandelt die Impulsfolge in ein quasikontinuierliches Signal um. Das kontinuierliche System-Ausgangssignal wird über einen Abtaster als Ausgangsfolge definiert.

Die s-Übertragungsfunktion des Haltegliedes ${\displaystyle G_{H}(s)}$ nullter Ordnung lautet: ^{[Einzelnachweise 13]}

${\displaystyle G_{H}(s)={\frac {{\bar {U}}(s)}{{\hat {U}}(s)}}={\frac {1-\mathrm {e} ^{T_{\mathrm {A} }\cdot s}}{s}}}$

Die z-Übertragungsfunktion (Impulsübertragungsfunktion) des Haltegliedes ${\displaystyle G_{H}(s)}$ und der Regelstrecke ${\displaystyle G_{S}(s)}$ wird durch die z-Transformation von ${\displaystyle {\mathcal {Z}}\{G_{H}(s)\cdot G_{S}(s)\}}$ berechnet.

Die z-Übertragungsfunktion von Halteglied und Regelstrecke lautet:

${\displaystyle G_{HS}(z)=\left.{\mathcal {Z}}\{G_{H}(s)\cdot G_{S}(s)\right|_{t=kT_{\mathrm {A} }}\}={\mathcal {Z}}\{G_{H}(s)\cdot G_{S}(s)\}}$

In diese Gleichung wird ${\displaystyle G_{H}(s)}$ eingesetzt:

${\displaystyle G_{HS}(z)={\mathcal {Z}}{\biggl \{}{\frac {1-\mathrm {e} ^{-T_{\mathrm {A} }s}}{s}}\cdot G_{S}(s){\biggr \}}={\mathcal {Z}}{\biggl \{}{\frac {G_{S}(s)}{s}}{\biggr \}}-{\mathcal {Z}}{\biggl \{}{\frac {\mathrm {e} ^{-T_{\mathrm {A} }s}\cdot G_{S}(s)}{s}}{\biggr \}}}$

Eine Multiplikation mit ${\displaystyle \mathrm {e} ^{-sT_{\mathrm {A} }}}$ entspricht im z-Bereich eine Rechtsverschiebung um einen Abtastzyklus ${\displaystyle T_{\mathrm {A} }}$ und damit einer Multiplikation mit ${\displaystyle z^{-1}}$.

${\displaystyle G_{HS}(z)={\mathcal {Z}}{\biggl \{}{\frac {1-\mathrm {e} ^{-T_{\mathrm {A} }s}}{s}}\cdot G_{S}(s){\biggr \}}=(1-z^{-1})\cdot {\mathcal {Z}}{\biggl \{}{\frac {G_{S}(s)}{s}}{\biggr \}}}$

Die z-Übertragungsfunktion der Reihenschaltung eines Haltegliedes nullter Ordnung mit einem kontinuierlichen System ergibt sich aus der Laplace-Transformierten der Sprungantwort ${\displaystyle G_{S}(s)}$, multipliziert mit ${\displaystyle {\frac {z-1}{z}}}$. (Siehe Tabelle ${\displaystyle {\frac {1}{s}}\ \circ \!\!-\!\!\bullet \ {\frac {z}{z-1}}}$):

${\displaystyle G_{HS}(z)={\frac {Y{(z)}}{U{(z)}}}={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}{\frac {G_{S}(s)}{s}}{\biggr \}}}$

Analog wie bei der Regelstrecke ${\displaystyle G_{S}(s)}$ kann für die im 2. Teil des Bildes dargestellte Anordnung der Funktionsblöcke Abtaster, Regelalgorithmus des Reglers und Halteglied die gleiche Form der Gleichung der z-Transformation benutzt werden. Ein- und Ausgangsgröße und die Systemgröße des Reglers ${\displaystyle G_{R}(s)}$ werden getauscht:

${\displaystyle G_{HR}(z)={\frac {U{(z)}}{E{(z)}}}={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}{\frac {G_{R}(s)}{s}}{\biggr \}}}$

Um die z-Transformation des kontinuierlichen Systems ${\displaystyle G(s)}$ bilden zu können, werden die Korrespondenztabellen angewendet. Steht für die gegebene s-Übertragungsfunktion ${\displaystyle G(s)}$ kein Eintrag für die z-Transformation zur Verfügung, muss eine Partialbruchzerlegung von ${\displaystyle G(s)/s}$ vorgenommen werden.

Beispiel: z-Transformation eines ${\displaystyle IT_{1}}$-Gliedes.

${\displaystyle G(s)={\frac {1}{s\cdot (s+1)}}}$

Gesucht z-Übertragungsfunktion ${\displaystyle G_{HS}(z)}$ des kombinierten Systems:

${\displaystyle G_{HS}(z)={\frac {Y{(z)}}{U{(z)}}}={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}{\frac {1}{s^{2}\cdot (s+1)}}{\biggr \}}}$

Partialbruchzerlegung von

${\displaystyle {\frac {1}{s^{2}\cdot (1+s)}}={\frac {1}{s^{2}}}-{\frac {1}{s}}+{\frac {1}{(s+1)}}}$

z-Transformation der Partialbrüche in den z-Bereich:

${\displaystyle G_{HS}(z)={\frac {Y{(z)}}{U{(z)}}}={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}{\frac {1}{s^{2}}}-{\frac {1}{s}}+{\frac {1}{(s+1)}}{\biggr \}}={\frac {z-1}{z}}\cdot {\biggl \{}{\frac {T_{\mathrm {A} }\cdot z}{(z-1)^{2}}}-{\frac {z}{z-1}}+{\frac {z}{z-\mathrm {e} ^{-T_{\mathrm {A} }}}}{\biggr \}}}$

Durch Ausmultiplizieren der Brüche ergibt sich die z-Transformation:

${\displaystyle G_{HS}(z)={\frac {Y(z)}{U(z)}}={\frac {T_{\mathrm {A} }}{z-1}}-1+{\frac {z-1}{z-\mathrm {e} ^{-T_{\mathrm {A} }}}}}$

Z-Übertragungsfunktionen der Standardregler

Es gelten hier allgemein die formalen Begriffe der Ein- und Ausgangsgrößen der Systemtheorie: Eingangssignal = ${\displaystyle U(z)}$, Ausgangssignal ${\displaystyle Y(z)}$. Für die Belange der Regler gelten die Eingangs- und Ausgangsgrößen des Reglers zu einem Regelkreis lauten: ${\displaystyle E(z)}$ und ${\displaystyle U(z)}$.

Die Regelalgorithmen mit den allgemeinen Koeffizienten lauten nach der rekursiven Rechenvorschrift: ^{[Einzelnachweise 14]}

${\displaystyle y_{(k)}=a_{1}\cdot y_{(k-1)}+b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}}$

Die z-Transformation der Differenzengleichung liefert die z-Übertragungsfunktion G_R(z) des Reglers:

${\displaystyle G_{R}(z)={\frac {Y(z)}{U(z)}}={\frac {b_{0}+b_{1}\cdot z^{-1}+b_{2}\cdot z^{-2}}{1-a_{1}\cdot z^{-1}}}={\frac {b_{0}\cdot z^{2}+b_{1}\cdot z+b_{2}}{z^{2}-a_{1}\cdot z}}}$

Tabelle der z-Übertragungsfunktionen der Standardregler (Typ II, Obersumme)

(a_i = Koeffizienten des Nennerpolynoms, b_i = Koeffizienten der Zählerpolynoms, T_I = T_N = 1 / K_I = Zeitkonstante = Nachstellzeit, T_V = Vorhaltezeit, T_A = Abtastzeit)

Reglerart	z-Übertragungsfunktion GR(z) der Standardregler
P-Regler	${\displaystyle G_{R}(z)=b_{0},\ b_{0}=K_{R}}$
I-Regler	${\displaystyle G_{R}(z)={\frac {b_{0}\cdot z}{z-a_{1}}}={\frac {b_{0}}{1-a_{1}\cdot z^{-1}}}}$ ${\displaystyle a_{1}=1;\ b_{0}=K_{\mathrm {I} }\cdot T_{\mathrm {A} }}$
PD-Regler	${\displaystyle G_{R}(z)={\frac {b_{0}\cdot z+b_{1}}{z}}=b_{0}+b_{1}\cdot z^{-1}}$ ${\displaystyle b_{0}=K_{R}\cdot \left[1+{\frac {T_{\mathrm {V} }}{T_{\mathrm {A} }}}\right];\ b_{1}=-K_{R}\cdot {\frac {T_{\mathrm {V} }}{T_{\mathrm {A} }}}}$
PI-Regler	${\displaystyle G_{R}(z)={\frac {b_{0}\cdot z+b_{1}}{z-a_{1}}}={\frac {b_{0}+b_{1}\cdot z^{-1}}{1-a_{1}\cdot z^{-1}}}}$ ${\displaystyle a_{1}=1;\ b_{0}=K_{R}\cdot \left[1+{\frac {T_{\mathrm {A} }}{T_{\mathrm {N} }}}\right];\ b_{1}=-K_{R}}$
PID-Regler	${\displaystyle G_{R}(z)={\frac {b_{0}\cdot z^{2}+b_{1}\cdot z+b_{2}}{z^{2}-a_{1}\cdot z}}={\frac {b_{0}+b_{1}\cdot z^{-1}+b_{2}\cdot z^{-2}}{1-a_{1}\cdot z^{-1}}}}$ ${\displaystyle a_{1}=1;\ b_{0}=K_{R}\cdot \left[1+{\frac {T_{\mathrm {A} }}{T_{\mathrm {N} }}}+{\frac {T_{\mathrm {V} }}{T_{\mathrm {A} }}}\right];\ b_{1}=-K_{R}\cdot \left[1+2\cdot {\frac {T_{\mathrm {V} }}{T_{\mathrm {A} }}}\right];\ b_{2}=K_{R}\cdot {\frac {T_{\mathrm {V} }}{T_{\mathrm {A} }}}}$

Umwandlung einer z-Übertragungsfunktion in eine Differenzengleichung

Eine gegebene z-Übertragungsfunktion lässt sich in eine Differenzengleichung umwandeln. Dazu sind folgende Schritte erforderlich.^{[Einzelnachweise 15]}

Die Übertragungsfunktion wurde durch den Koeffizienten ${\displaystyle a_{n}}$ dividiert, um ${\displaystyle z^{n}}$ freistellen zu können.

Diese Form der Übertragungsfunktion wurde entsprechend der dargestellten Koeffizienten wie folgt neu geordnet.

${\displaystyle G(z)={\frac {Y(z)}{U(z)}}={\frac {b_{m}\cdot z^{m}+b_{m-1}\cdot z^{m-1}+b_{m-2}\cdot z^{m-2}\cdots +b_{1}\cdot z+b_{0}}{z^{n}+a_{n-1}\cdot z^{n-1}+a_{n-2}\cdot z^{n-2}+\cdots +a_{1}\cdot z+a_{0}}}={\frac {{\text{Zähler}}(z)}{{\text{Nenner}}(z)}}}$

• Die Systemausgangsgröße Y(z) und die Systemeingangsgröße U(z) werden kreuzweise mit den Polynomen der z-Übertragungsfunktion multipliziert:

${\displaystyle {b_{m}\cdot z^{m}\cdot U(z)+b_{m-1}\cdot z^{m-1}\cdot U(z)+b_{m-2}\cdot z^{m-2}\cdot U(z)+\cdots +b_{1}\cdot z\cdot U(z)+b_{0}\cdot U(z)=z^{n}\cdot Y(z)+a_{n-1}\cdot z^{n-1}\cdot Y(z)+a_{n-2}\cdot z^{n-2}\cdot Y(z)+\cdots +a_{1}\cdot z\cdot Y(z)+a_{0}\cdot Y(z)}}$

• Die Zähler- und Nennerpolynome werden durch die höchste Potenz von z dividiert:

${\displaystyle {b_{m}\cdot z^{-(n-m)}\cdot U(z)+b_{m-1}\cdot z^{-(n-m+1)}\cdot U(z)+b_{m-2}\cdot z^{-(n-m+2)}\cdot U(z)+\cdots +b_{0}\cdot z^{-n}\cdot U(z)=Y(z)+a_{1}\cdot z^{-(n-1)}\cdot Y(z)+a_{2}\cdot z^{-(n-2)}\cdot Y(z)+a_{0}\cdot z^{-n}\cdot Y(z)}}$

• Mit der Anwendung des Rechtsverschiebungssatzes der z-Transformation entsteht die Differenzengleichung:

${\displaystyle {b_{m}\cdot u[k-n+m]+b_{m-1}\cdot u[k-n+m-1]+\dots +b_{1}\cdot u[k-n+1]+b_{0}\cdot u[k-n]=y[k]+a_{n-1}\cdot y[k-1]+\dots +a_{1}\cdot y[k-n+1]+a_{0}\cdot y[k-n]}}$

• Die Differenzengleichung wird nach y(k) aufgelöst. Damit entsteht eine Rekursionsgleichung zur Berechnung der Ausgangsgröße ${\displaystyle y_{(k)}}$ des Systems für beliebige Eingangssignale ${\displaystyle u_{(k)}}$.

${\displaystyle y_{k}=-a_{n-1}\cdot y_{(k-1)}-\dots -a_{1}\cdot y_{(k-n+1)}-a_{0}\cdot y_{(k-n)}+b_{m}\cdot u_{(k-n+m)}+\dots +b_{1}\cdot u_{(k-n+1)}+b_{0}\cdot u_{(k-n)}}$

Rücktransformation in den diskreten Zeitbereich f(kT_A)

Für die Programmierung des Mikrocomputers des Digitalreglers werden Differenzengleichungen benötigt, die durch Überführung der z-Übertragungsfunktion des z-Bildbereiches in den diskreten Zeitbereich f(k) gewonnen wird.

Die inverse z-Transformation liefert für F(z) wieder die Werte der Zahlenfolge:

${\displaystyle {\mathcal {Z}}^{-1}\{F(z)\}=f(kT_{\mathrm {A} })}$ für ${\displaystyle k=(0;1;2;3;\ldots )}$.^{[Einzelnachweise 16]}

Dazu sind drei Verfahren gegeben:

• Rücktransformation durch Polynomdivision,

Durch die Polynomdivision wird die z-Transformierte ${\displaystyle F(z)}$ in eine konvergierende Potenzreihe nach ${\displaystyle z^{-i}}$ entwickelt. Dividiert man das Zählerpolynom von ${\displaystyle F(z)}$ durch das Nennerpolynom nach den Regeln der Polynomdivision, so ergibt sich die gewünschte Potenzreihe. Die Vorfaktoren der Potenzen von z sind die gesuchten Werte der Zahlenfolge ${\displaystyle f(kT_{\mathrm {A} })}$.

• Partialbruchzerlegung

Die Rücktransformation von ${\displaystyle F(z)}$ erfolgt durch die Partialbruchzerlegung mit Hilfe der zugehörigen Korrespondenztabelle. Die Partialbrüche sollen die Form ${\displaystyle {\frac {z}{z-z_{i}}}}$ haben. Die inverse z-Transformation ergibt ${\displaystyle f(kT_{\mathrm {A} })}$ als Summe der rücktransformierten Partialbrüche.

• Auswertung des Umkehrintegrals (Residuensatz)

Die inverse z-Transformation ist über das komplexe Umlaufintegral bestimmt. Die Lösung des Integrals lässt sich auf die Bestimmung der Residuen ${\displaystyle \operatorname {Res} \{z_{i}\}}$ zurückführen.

${\displaystyle f(kT_{\mathrm {A} })=\sum _{i}\operatorname {Res} \{F(z)\cdot z^{k-1}\}\quad |_{Z=Z_{i}}}$

Berechnungsbeispiele zur z-Transformation

Beispiel 1: z-Transformierte der Sprungfunktion der Eingangsgröße ${\displaystyle u_{\sigma }(t)}$:

Die z-Transformierte der normierten Sprungfunktion ${\displaystyle u_{\sigma }(t)=1}$ für ${\displaystyle t>0}$ ist zu ermitteln. Lösung: Die kontinuierliche Eingangsgröße ${\displaystyle u(t)}$ wird als Sprungfunktion (Einheitssprung) zum Zeitpunkt ${\displaystyle t=0}$ mit dem Wert 1 abgetastet. Durch Abtastung entsteht eine Wertefolge mit konstanten Amplituden = 1. ${\displaystyle u(kT_{\mathrm {A} })=u_{(k)}=0(-1),1(0),1(T_{\mathrm {A} }),1(2T_{\mathrm {A} }),1(3T_{\mathrm {A} })\dots }$ oder die Impulsfolgefunktion: ${\displaystyle u^{*}(t)=\sum _{k=0}^{\infty }u_{(k)}\cdot \delta (t-kT_{\mathrm {A} })}$ Die z-Transformation lautet damit: ${\displaystyle {\mathcal {Z}}\{u_{k}\}=u(z)=\sum _{k=0}^{\infty }u_{k}\cdot z^{-k}=\sum _{k=0}^{\infty }z^{-k}\quad \quad {\text{mit}}\ u_{k}=1}$ Der Grenzwert für ${\displaystyle z^{-n}}$ für ${\displaystyle n\to \infty }$ und ${\displaystyle |z|>1}$ (Konvergenz) ist Null. Die z-Transformierte der Einheitssprungfunktion ist damit: ${\displaystyle {\mathcal {Z}}\{u_{k}\}=u(z)=\sum _{k=0}^{\infty }u_{k}\cdot z^{-k}={\frac {z}{z-1}}}$

Beispiel 2: z-Transformierte des Produktes einer Exponentialfunktion f(t) mit dem Einheitssprung u(t)=1:

Gegeben: Exponentialfunktion ${\displaystyle y(t)=\mathrm {e} ^{-t/T_{1}}}$ Einheitssprung ${\displaystyle u_{\sigma }}$ = 1 für t>0. Gesucht: Ergebnis der beiden Beziehungen als Produkt im z-Bereich: Die Ausgangswertefolge ${\displaystyle y(kT_{\mathrm {A} })}$ lautet: ${\displaystyle y(kT_{\mathrm {A} })=y_{(k)}=\mathrm {e} ^{-{\frac {kT_{\mathrm {A} }}{T_{1}}}}}$ Daraus ergibt sich die z-Transformierte: ${\displaystyle y(z)=\sum _{k=0}^{\infty }y_{k}\cdot z^{-k}=\sum _{k=0}^{\infty }\mathrm {e} ^{-{\frac {kT_{\mathrm {A} }}{T_{1}}}}\cdot z^{-k}}$ Substituiert man ${\displaystyle z^{'}=z\cdot \mathrm {e} ^{T_{\mathrm {A} }/T_{1}},\quad (z^{'})^{-k}=z^{-k}\cdot \mathrm {e} ^{-kT_{\mathrm {A} }/T_{1}}}$, so lautet die z-Transformierte ${\displaystyle y(z)={\mathcal {Z}}\{y(kT_{\mathrm {A} })\}={\mathcal {Z}}\{\mathrm {e} ^{-kT_{\mathrm {A} }/T_{1}}\}={\frac {z}{z-\mathrm {e} ^{-T_{\mathrm {A} }/T_{1}}}}}$

Beispiel 3: Ermittlung der z-Übertragungsfunktion aus einem Verzögerungsglied 1. Ordnung

Gegeben: Übertragungsfunktion G(s) des PT1-Gliedes mit der Verstärkung ${\displaystyle K}$ und der Zeitkonstante T1: ${\displaystyle G(s)={\frac {Y(s)}{U(s)}}={\frac {K}{1+s\cdot {T_{1}}}}={\frac {K\cdot a}{s+a}};\qquad a=1/T_{1};-1/T_{1}=}$ Nullstelle des Nennerpolynoms. Anmerkung: Die Zeitkonstantendarstellung der Übertragungsfunktion ist der Pol-Nullstellendarstellung mathematisch identisch. Gesucht: z-Übertragungsfunktion ${\displaystyle G(z)}$ aus ${\displaystyle G(s)}$. Dazu wird zuerst die Gewichtsfunktion ${\displaystyle g(t)}$ des PT1-Gliedes ermittelt. Aus einer Laplace-Korrespondenztabelle findet man für das Zeitverhalten ${\displaystyle f(t)}$ der Übertragungsfunktion ${\displaystyle G(s)}$ für die Gewichtsfunktion (Impulsantwort): ${\displaystyle g(t)={\mathcal {L}}^{-1}\{G(s)\}={\mathcal {L}}^{-1}{\bigg \{}\underbrace {\frac {1}{1+T_{1}\cdot s}} _{\text{s-Bereich}}{\bigg \}}=\underbrace {{\frac {1}{T_{1}}}\cdot \mathrm {e} ^{-{\frac {t}{T_{1}}}}} _{\text{Zeitbereich}}\qquad {\text{oder}}\qquad {\mathcal {L}}^{-1}{\bigg \{}\underbrace {\frac {1}{s+a}} _{\text{s-Bereich}}{\bigg \}}=\underbrace {\mathrm {e} ^{-a\cdot t}} _{\text{Zeitbereich}}}$. Die Verstärkung ${\displaystyle K}$ wurde für den Transfer in den Zeitbereich nicht berücksichtigt und wird wieder eingesetzt. ${\displaystyle g(t)=K\cdot {\mathcal {L}}^{-1}\{G(s)\}=K\cdot {\mathcal {L}}^{-1}{\bigg \{}{\frac {1}{1+T_{1}\cdot s}}{\bigg \}}={\frac {K}{T_{1}}}\cdot \mathrm {e} ^{-{\frac {t}{T_{1}}}}={\frac {K}{T_{1}}}\cdot \mathrm {e} ^{-a\cdot t}}$ Für die Eingangsimpulsfolge ${\displaystyle g(kT_{\mathrm {A} })}$ wird die z-Transformation angewendet. Aus einer in Fachbüchern der Regelungstechnik dargestellten Korrespondenztabelle wird für ${\displaystyle f(t)=\mathrm {e} ^{-a\cdot t}}$ als Gewichtsfunktion (Impulsantwort) die zugehörige F(z)-Funktion entnommen. Der Faktor ${\displaystyle K/T_{1}}$ hat keine Auswirkungen auf die Transformation und wird später berücksichtigt: ${\displaystyle {\mathcal {Z}}\{\mathrm {e} ^{-at}\}{\bigg |}_{t=kT_{\mathrm {A} }}={\frac {z}{z-\mathrm {e} ^{-a\cdot T_{\mathrm {A} }}}};\qquad T_{\mathrm {A} }={\text{Abtastzeit}};\quad k={\text{Abtastfolge}}}$ Daraus ergibt sich unter Berücksichtigung des Faktors ${\displaystyle K/T_{1}}$ die gesuchte z-Übertragungsfunktion, die gerne vereinfacht dargestellt wird: ${\displaystyle G(z)={\frac {K}{T_{1}}}\cdot {\mathcal {Z}}\{g(kT_{\mathrm {A} })\}={\frac {K}{T_{1}}}\cdot {\frac {z}{z-a_{1}}};\qquad {\text{mit }}a_{1}=\mathrm {e} ^{-{\frac {T_{\mathrm {A} }}{T_{1}}}};\quad T_{1}=1/a}$

Beispiel 4: z-Übertragungsfunktion einer Differenzengleichung für den Integralalgorithmus:

Definition der Signale: Analoge Regeldifferenz = ${\displaystyle e(t)}$, Abgetastete Regeldifferenz = ${\displaystyle e_{(k)}}$, Reglerausgangsgröße = ${\displaystyle u_{(k)}}$, Zeitkonstante ${\displaystyle K_{I}=1/T_{N}}$. Gegeben: Differenzengleichung: ${\displaystyle u_{(k)}=u_{(k-1)}+K_{I}\cdot T_{\mathrm {A} }\cdot e_{(k-1)}}$ (Differenzengleichung nach Euler-Vorwärts, wegen ${\displaystyle e_{(k-1)}}$) entsteht „Untersumme“. Gesucht: z-Übertragungsfunktion. Nach der Transformationsvorschrift ändern sich die Größen: ${\displaystyle u_{(k)}\longrightarrow U(z),\qquad u_{(k-1)}\longrightarrow z^{-1}\cdot U(z),\qquad e_{(k-1)}\longrightarrow z^{-1}\cdot E(z).}$ Daraus folgt für die z-Transformation: ${\displaystyle U(z)=z^{-1}\cdot U(z)+K_{I}\cdot T_{\mathrm {A} }\cdot z^{-1}\cdot E(z)}$ Wird U(z) / E(z) ausgeklammert, entsteht die z-Übertragungsfunktion des Integralalgorithmus: ${\displaystyle G_{R}(z)={\frac {U(z)}{E(z)}}={\frac {K_{I}\cdot T_{\mathrm {A} }\cdot z{-1}}{1-z^{-1}}}={\frac {K_{I}\cdot T_{\mathrm {A} }}{z-1}}}$ Für die gleiche Differenzengleichung des Integrationsalgorithmus nach Euler-Rückwärts (Obersumme): ${\displaystyle u_{(k)}=u_{(k-1)}+K_{I}\cdot T_{\mathrm {A} }\cdot e_{(k)}}$ lautet die z-Übertragungsfunktion mit ${\displaystyle e_{(k)}\to E(z)}$: ${\displaystyle G_{R}(z)={\frac {U{(z)}}{E{(z)}}}={\frac {K_{I}\cdot T_{\mathrm {A} }}{1-z^{-1}}}}$ Aus der Übertragungsfunktion ${\displaystyle G_{R}(z)}$ wird die Stellgröße des Reglers ${\displaystyle U(z)}$ abgeleitet mit der Regelabweichung ${\displaystyle E(z)=W(z)-Y(z)}$:

Anwendung der z-Übertragungsfunktion für einen digitalen PI-Regler mit Abtastfunktion und Halteglied

Das nachfolgende Berechnungsbeispiel zeigt die über die z-Transformation ermittelte Differenzengleichung eines digitalen PI-Reglers im Vergleich mit den Differenzengleichungen nach Euler-Rückwärts.

Digitale Regler in industriellen Erzeugnissen werden gegenüber analogen Reglern zunehmend in großen Stückzahlen produziert. Dafür sind verschiedene Gründe gegeben:

• Die Integrationsrate der Mikrorechner hat soweit zugenommen, dass die Schnittstellen wie AD- und DA-Wandler wie auch Haltefunktionen Bestandteil eines einzigen hochintegrierten Bausteins sind.
• Kostengünstige Produktion der Hardware und deren Prüfung,
• Jederzeit - vor Anlagen-Auslieferung - können per Software Parameteränderungen oder Regler-Struktur-Änderungen durchgeführt werden.

Mit der Anwendung der z-Transformation auf abgetastete Signale und des gewünschten Regelalgorithmus entsteht die z-Übertragungsfunktion.

Die Hauptaufgabe der Realisierung eines digitalen Reglers ist die Aufstellung der z-Übertragungsfunktion des Reglers bzw. das Finden der zur Programmierung des Mikrocomputers benötigten Rekursionsgleichung. Das nachstehende Berechnungsbeispiel aus einem Fachbuch zeigt einen digitalen PI-Regler, der durch eine Reihenschaltung von Halteglied, Reglerfunktion G_R(s) und Abtaster approximiert wird.

Die gesuchte z-Übertragungsfunktion des digitalen Reglers D(z) besteht aus dem Produkt von Halteglied ${\displaystyle H_{0}(z)={\frac {z-1}{z}}}$ und Reglerfunktion G_R(s):

${\displaystyle D(z)={\frac {U{(z)}}{E{(z)}}}={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}{\frac {G_{R}(s)}{s}}{\biggr \}}}$

Berechnungsbeispiel eines PI-Reglers als Reihenschaltung von idealem Abtaster, PI-Regleralgorithmus und Halteglied.^{[Einzelnachweise 17]}

Gegeben: s-Übertragungsfunktion eines PI-Reglers GR: ${\displaystyle G_{R}(s)={\frac {U{(s)}}{E{(s)}}}={\frac {K_{P}\cdot (1+T_{N}\cdot s)}{T_{N}\cdot s}}=K_{P}+{\frac {K_{P}}{T_{N}\cdot s}}}$ Parameter des PI-Reglers mit folgenden Zahlenwerten: Verstärkung: ${\displaystyle K_{P}=2}$; Zeitkonstante: ${\displaystyle T_{N}=1{,}5[s]}$; Abtastzeit: ${\displaystyle T_{\mathrm {A} }=0{,}1[s]}$; Gesucht: z-Übertragungsfunktion und daraus die Differenzengleichung mit dem Regelalgorithmus des PI-Reglers: ${\displaystyle D(z)={\frac {U(z)}{E(z)}}=H_{0}(z)\cdot {\mathcal {Z}}{\biggl \{}{\frac {G_{R}(s)}{s}}{\biggr \}}}$ Nach Anwendung der oben stehenden abgeleiteten Gleichung mit Eintrag der PI-Komponenten für ${\displaystyle G_{R}(s)}$ müssen die Komponenten des s-Bereichs in den z-Bereich transformiert werden: ${\displaystyle D(z)={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}{\frac {K_{P}}{s}}+{\frac {K_{P}}{T_{N}\cdot s^{2}}}{\biggr \}}={\frac {z-1}{z}}\cdot {\mathcal {Z}}{\biggl \{}K_{P}\cdot {\frac {1}{s}}+{\frac {K_{P}}{T_{N}}}\cdot {\frac {1}{s^{2}}}{\biggr \}}}$ Die Terme des s-Bereichs werden z-transformiert: ${\displaystyle D(z)={\frac {z-1}{z}}\cdot {\biggl \{}K_{P}\cdot {\frac {z}{z-1}}+{\frac {K_{P}}{T_{N}}}\cdot {\frac {T_{\mathrm {A} }\cdot z}{(z-1)^{2}}}{\biggr \}}={\frac {K_{P}\cdot T_{N}+K_{P}\cdot (T_{\mathrm {A} }-T_{N})\cdot z^{-1}}{T_{N}-T_{N}\cdot z^{-1}}}}$ Damit lautet die z-Übertragungsfunktion des Reglers mit Zahlenwerten: ${\displaystyle D(z)={\frac {U{(z)}}{E{(z)}}}={\frac {3-2{,}8\cdot z^{-1}}{1{,}5-1{,}5\cdot z^{-1}}}={\frac {2-1{,}8667\cdot z^{-1}}{1-z^{-1}}}}$ Diese z-Übertragungsfunktion wird in Operatorendarstellung nach U(z) geordnet und als Differenzengleichung ${\displaystyle u_{(k)}}$ im Mikroprozessor programmiert. ${\displaystyle U(z)\cdot (1-z^{-1})=E(z)\cdot (2-1{,}8667\cdot z^{-1})}$ ${\displaystyle U(z)-z^{-1}\cdot U(z)=2\cdot E(z)-1{,}8667\cdot z^{-1}\cdot E(z)}$ Durch Anwendung der Rechtsverschiebung um einen Abtastschritt „-1“ ergibt sich für Rücktransformation in den diskreten Zeitbereich die Differenzengleichung ${\displaystyle u_{(k)}}$. ${\displaystyle u_{(kT_{\mathrm {A} })}-u_{(kT_{\mathrm {A} }-1T_{\mathrm {A} })}=2\cdot e_{(kT_{\mathrm {A} })}-1{,}8667\cdot e{(kT_{\mathrm {A} }-1T_{\mathrm {A} })}}$ Diese Gleichung nach ${\displaystyle u_{(kT_{\mathrm {A} })}}$ aufgelöst ergibt: ${\displaystyle u_{(kT_{\mathrm {A} })}=u_{(kT_{\mathrm {A} }-T_{\mathrm {A} })}+2\cdot e_{(kT_{\mathrm {A} })}-1{,}8667\cdot e_{(kT_{\mathrm {A} }-T_{\mathrm {A} })}}$ In vereinfachter Schreibweise lautet die Differenzengleichung eines PI-Reglers für ein abgetastetes Regelsystem mit Halteglied bei TA = 0,1 [s]: ${\displaystyle u_{(k)}=u_{(k-1)}+2\cdot e_{(k)}-1{,}8667\cdot e_{(k-1)}}$ Zum Vergleich die errechnete Differenzengleichung für TA = 0,01 [s] zur besseren Annäherung an die analytische Funktion: ${\displaystyle u_{(k)}=u_{(k-1)}+2\cdot e_{(k)}-1{,}9867\cdot e_{(k-1)}}$

Tabelle zur grafischen Darstellung der Sprungantwort des PI-Reglers mit T_A = 0,1 [s] und e_(k) = 1,
im Vergleich mit einer direkten Anwendung von Differenzengleichungen nach Euler-Rückwärts.

Folge k	Zeit TA [sec]	Differenzengleichung aus z-Transformation Ausgangssignal ${\displaystyle u_{(k)}}$	Differenzengleichung Euler-Rückwärts ${\displaystyle u_{(k)}}$ Untersumme	Differenzengleichung Euler-Rückwärts ${\displaystyle u_{(k)}}$ Obersumme
0	0	${\displaystyle u_{(k)}=0+2\cdot 1-1{,}8667\cdot 0=2{,}0000}$	2,0000	2,1333
1	0,1	${\displaystyle u_{(k)}=2{,}0000+2\cdot 1-1{,}8667\cdot 1=2{,}1333}$	2,1333	2,2667
2	0,2	${\displaystyle u_{(k)}=2{,}1333+2\cdot 1-1{,}8667\cdot 1=2{,}2666}$	2,2667	2,4000
3	0,3	${\displaystyle u_{(k)}=2{,}2666+2\cdot 1-1{,}8667\cdot 1=2{,}3999}$	2,4000	2,5333
4	0,4	${\displaystyle u_{(k)}=2{,}3999+2\cdot 1-1{,}8667\cdot 1=2{,}5332}$	2,5333	2,6667
5	0,5	${\displaystyle u_{(k)}=2{,}5332+2\cdot 1-1{,}8667\cdot 1=2{,}6665}$	2,6667	2,8000
6	0,6	${\displaystyle u_{(k)}=2{,}6665+2\cdot 1-1{,}8667\cdot 1=2{,}7998}$	2,8000	2,9333
10	1,0	3,3330	3,3330	3,4667
15	1,5	3,9995	4,0000	4,1333

Qualitativer Vergleich zwischen PI-Reglern mit Differenzengleichungen über die z-Transformation und Differenzengleichungen nach Euler-Rückwärts

• Schnittstelle des Rechenbeispiels:

Das Fachbuch-Rechenbeispiel der Bestimmung der Differenzengleichung eines PI-Reglers über die z-Transformation ist offensichtlich als Untersumme definiert. Dieses Beispiel setzt ideale Schnittstellen mit einem Halteglied nullter Ordnung (entspricht einem Zeitschritt T_A) und einen idealen Mikrorechner voraus.

• Differenzengleichungen als Funktion der Ober- und Untersumme:

Die Grafik zeigt den Unterschied der Stellgröße für die Berechnungsmethoden der Differenzengleichungen nach der Ober- und Untersumme.

Die grafische Darstellung der Sprungantwort des PI-Reglers laut der Tabellen-Berechnungspunkte ${\displaystyle y_{(k)}}$ entsprechen einer Rechteckfunktion, weil am Reglerausgang für die Wertefolge ein Halteglied für den Zeitraum T_A wirkt, das nach jedem Rechenschritt gelöscht wird. Die errechneten Daten der Differenzengleichung über die z-Transformation und die Daten nach den Differenzengleichungen Euler-Rückwärts-Untersumme sind identisch.

Sowohl die errechneten Ausgangsgrößen des Reglers der Differenzengleichung als Wertefolgen ${\displaystyle y_{(k)}}$ über die z-Übertragungsfunktion wie auch die errechneten Wertefolgen der Ausgangsgrößen ${\displaystyle y_{(k)}}$ nach den Differenzengleichungen der Methode Euler-Rückwärts (Untersumme und Obersumme) entsprechen nur dann der analytischen Funktion der Sprungantwort des PI-Reglers, wenn die Abtastzeit ${\displaystyle T_{\mathrm {A} }=\Delta t}$ gegen Null geht.

• Verwendung der Differenzengleichungen der Standardregler ohne z-Transformation möglich:

Der Vergleich der Rechenergebnisse führt zu der Auffassung, dass für die Bestimmung der Differenzengleichungen der Standardregler die im Abschnitt Tabelle der Differenzengleichungen der Standardregler (Euler Rückwärts) aufgeführten Differenzengleichungen unmittelbar ohne z-Transformation verwendet werden können.

Aus der Übertragungsfunktion des s-Bereiches wird deutlich, dass der PI-Regler in der Reihenstruktur aus einem I-Glied und einem PD1-Glied besteht.

Übertragungsfunktion des PI-Reglers in der Parallelstruktur:

${\displaystyle {\frac {U}{E}}{(s)}=K_{P}+{\frac {K_{P}}{T_{N}\cdot s}}=K_{P}\left(1+{\frac {1}{T_{N}\cdot s}}\right)}$

Wird der Klammerausdruck der Gleichung auf einen gemeinsamen Nenner gebracht, entsteht die Produktdarstellung in der Reihenstruktur:

${\displaystyle {\frac {U}{E}}{(s)}=K_{P}{\frac {T_{N}\cdot s+1}{T_{N}\cdot s}}=G_{I}(s)\cdot G_{PD}(s)={\frac {K_{P}}{T_{N}\cdot s}}\cdot (T_{N}\cdot s+1)}$

K_PI = K_P / T_N ist die Verstärkung des PI-Reglers.

Für die Berechnung des PI-Reglers werden zwei Differenzengleichungen 1. Ordnung benötigt. Dabei ist wegen der empfohlenen Reihenschaltung die Ausgangsgröße des I-Gliedes die Eingangsgröße des PD1-Gliedes. Die Ausgangsgröße des PD-Gliedes im zeitdiskreten Bereich ist das Folgeglied zum Zeitpunkt ${\displaystyle k\cdot \Delta t}$. Die Eingangsgröße des PI-Reglers ist die normierte zeitdiskrete Sprungfunktion ${\displaystyle 1(t)=1(0);1(\Delta t);1(2\Delta t);1(3\Delta t);\dots }$.

Die Differenzengleichung eines PI-Reglers nach der Untersumme als Reihenschaltung von I-Glied und PD1-Glied lautet:

${\displaystyle {\text{I-Glied:}}\qquad e_{1(k)}=e_{1(k-1)}+{e_{(k)}\cdot K_{P}\cdot \Delta t}/{T_{N}}}$

${\displaystyle {\text{PD-Glied:}}\quad u_{(k)}=e_{1(k-1)}+[e_{1(k)}-e_{1(k-1)}]\cdot {T_{N}}/{\Delta t}}$

Anmerkung zum PD-Glied: ${\displaystyle e_{1(k-1)}}$ bedeutet wegen Untersumme: aktuelles ${\displaystyle e_{1(k)}}$ des I-Gliedes um einen Schritt (k-1) zurückgesetzt.

• Genauigkeit der Approximation des Regelalgorithmus des PI-Reglers:

Die Güte der Approximation ist durch das Verhältnis der Abtastzeit ${\displaystyle T_{\mathrm {A} }=\Delta t}$ zur dominanten Zeitkonstante ${\displaystyle T}$ des Reglers und der Regelstrecke bestimmt. Soll ein PD-Glied des PI-Reglers ein PT₁-Glied der Regelstrecke kompensieren, sollte dieses Verhältnis 0,1 bis 0,01 betragen.

Welche Genauigkeit des Regelvorgangs erreicht werden muss, hängt von der Vorgabe des Lastenheftes und von der Art der Regelstrecke ab.

• Reale Schnittstellen und reale Mikrorechner berücksichtigen:

Bei schnellen Regelstrecken können die realen Schnittstellen des Reglers durch die signaltechnischen Verzögerungen als Ersatztotzeit berücksichtigt werden. Im Gegensatz zur Laplace-Transformation kann eine z-transformierte Übertragungsfunktion mit einer Totzeit im Rahmen der Rechenregeln der z-Transformation durch Rückwärtsverschiebung „Verschiebung nach rechts“ um ${\displaystyle d=Tt/T_{\mathrm {A} }}$ Abtastschritte als komplette z-Übertragungsfunktion berechnet werden.

Einsatz von z-Transformation zur Bestimmung expliziter Formeln von Rekursionsvorschriften

Motivation

Die z-Transformation kann zur Bestimmung expliziter Formeln für Zahlenfolgen eingesetzt werden, die rekursiv definiert sind. Ein Paradebeispiel hierfür ist die Fibonacci-Zahlenfolge

${\displaystyle 0,1,1,2,3,5,8,13,\dots }$

Die Zahlenfolge ist rekursiv definiert und zwar mit der Rekursionsvorschrift

${\displaystyle y_{k}=y_{k-1}+y_{k-2},\quad k>1}$

und dem Rekursionsanfang

${\displaystyle y_{0}=0\quad {\text{und}}\quad y_{1}=1.}$

Die rekursive Definition ist einfach, hat jedoch zum Nachteil, dass sie es nicht erlaubt, das k-te Element der Zahlenfolge direkt zu bestimmen, ohne seine ${\displaystyle k-1}$ Vorgänger zu berechnen, was bei größer werdendem ${\displaystyle n}$ immer zeitintensiver wird. Man fragt sich also, ob nicht auch eine explizite Formel existiert, die eine direkte Bestimmung eines jeden Elements der Zahlenfolge erlaubt. Für Fibonacci-Zahlen existiert eine solche explizite Formel und sie lautet

${\displaystyle y_{k}={\frac {1}{\sqrt {5}}}\cdot \left(\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k}\right),\quad k\geq 0.}$.

Auf den ersten Blick scheint es unmöglich zu sein, dass diese Formel mit ${\displaystyle {\sqrt {5}}}$ Termen überhaupt ganze Zahlen erzeugt, doch durch Einsetzen von ${\displaystyle k=0,1,2,3,\dots }$ kann sich jeder selbst davon überzeugen, dass die Formel in der Tat die entsprechenden Fibonacci-Zahlen liefert.

Doch wie kommt man nur auf eine solche Formel? Dazu gibt es verschiedenen Methoden und die z-Transformation ist eine davon. Im Folgenden wird eine Methodik gezeigt, wie man mit Hilfe von z-Transformation die explizite Formel einer rekursiven Berechnungsvorschrift bestimmen kann. Die allgemeinen Ausführungen werden am Beispiel der Fibonacci-Zahlen angewendet und verständlich gemacht.

Allgemeine Form der Rekursionsgleichung

Differenzengleichung und Rekursion

Eine Rekursionsformel vom Typ

${\displaystyle y_{k}=a_{1}\cdot y_{k-1}+a_{2}\cdot y_{k-2}+\dots +a_{n}\cdot y_{k-n}\quad {\text{mit }}y_{k}=0{\text{ für }}k<0}$

kann als Beschreibung eines abgetasteten dynamischen Systems ohne Eingangssignal interpretiert werden, denn die weiter oben beschriebene Differenzengleichung

${\displaystyle {y_{(k)}=b_{0}\cdot u_{(k)}+b_{1}\cdot u_{(k-1)}+b_{2}\cdot u_{(k-2)}+\dots +b_{m}\cdot u_{(k-m)}\quad -a_{1}\cdot y_{(k-1)}-a_{2}\cdot y_{(k-2)}-\dots -a_{n}\cdot y_{(k-n)}}}$.

geht direkt in die Rekursionsformel über, wenn man das Eingangssignal ${\displaystyle u}$ zu Null setzt, d. h. ${\displaystyle u_{k}=0}$ für alle ${\displaystyle k}$:

${\displaystyle {y_{(k)}=-a_{1}\cdot y_{(k-1)}-a_{2}\cdot y_{(k-2)}-\dots -a_{n}\cdot y_{(k-n)}}.}$

Das bedeutet, dass eine Rekursionsformel als eine Art Eigendynamik des Systems betrachtet werden kann, wenn auf dieses keine äußeren Störungen einwirken. Die Eigendynamik wird allerdings erst sichtbar, wenn das System aus der Ruhelage ausgelenkt wird, und der genaue Verlauf der „Bewegung“ hängt von den Anfangsbedingungen ab. Man setzt also voraus, dass das System bis zum Zeitpunkt Null keinerlei Dynamik aufwies (d. h. ${\displaystyle y_{k}=0,\ \forall k<0}$), doch die Anfangsbedingungen (Rekursionsanfang) müssen unbedingt berücksichtigt werden.

Anfangsbedingungen und Rekursionsanfang

Um die Rekursionsformel mit Hilfe der z-Transformation lösen zu können, muss der Rekursionsanfang (also die Anfangsbedingung) in die Differenzengleichung eingefügt werden. Dies kann man mit Hilfe des zeitdiskreten Dirac-Impulses mit der Definition

${\displaystyle \delta _{k}={\begin{cases}1\ &{\text{falls }}k=0\\0\ &{\text{sonst}}\end{cases}}}$

umsetzen. Man platziert eine Reihe von ${\displaystyle n}$ diskreten ${\displaystyle \delta }$-Impulsen an den ersten ${\displaystyle n}$ Zeitpunkten

${\displaystyle {\begin{aligned}y_{k}&=a_{1}\cdot y_{k-1}+a_{2}\cdot y_{k-2}+\dots +a_{n}\cdot y_{k-n}\quad +d_{0}\cdot \delta _{k}+d_{1}\cdot \delta _{k-1}+d_{2}\cdot \delta _{k-2}+\dots +d_{n-1}\cdot \delta _{k-(n-1)}\\&=\sum _{i=1}^{n}a_{i}\cdot y_{k-i}\quad +\sum _{j=0}^{n-1}d_{j}\cdot \delta _{k-j}\end{aligned}}}$

und wählt deren Amplituden ${\displaystyle d_{i}}$ so, dass sich die gewünschten ${\displaystyle n}$ Anfangswerte der Zahlenfolge ergeben. Die Anzahl der Anfangswerte muss ${\displaystyle n}$ sein, damit die Rekursionsformel starten kann, denn ${\displaystyle n}$ ist die Anzahl der Rekursionselemente auf der rechten Seite der Rekursionsgleichung. Angabe weiterer Anfangswerte (mehr als ${\displaystyle n}$) ist überflüssig, weil diese Werte direkt aus der Rekursionsformel berechnet werden.

Unter Berücksichtigung, dass ${\displaystyle y_{k}=0}$ für alle negativen ${\displaystyle k}$ angesetzt ist und der diskrete Dirac-Impuls ${\displaystyle \delta _{k-j}}$ nur an der Stelle ${\displaystyle k=j}$ den Wert 1 hat und ansonsten 0, erhält man etwa für die ersten drei Elemente die Beziehungen:

${\displaystyle {\begin{aligned}y_{0}&=\sum _{i=1}^{n}a_{i}\cdot \underbrace {y_{0-i}} _{=0}+\sum _{j=0}^{n-1}d_{j}\cdot \delta _{0-j}=d_{0}\cdot \delta _{0}=d_{0}\\y_{1}&=\sum _{i=1}^{n}a_{i}\cdot y_{1-i}+\sum _{j=0}^{n-1}d_{j}\cdot \delta _{1-j}=a_{1}\cdot \underbrace {y_{0}} _{=d_{0}}+d_{1}=a_{1}\cdot d_{0}+d_{1}\\y_{2}&=\sum _{i=1}^{n}a_{i}\cdot y_{2-i}+\sum _{j=0}^{n-1}d_{j}\cdot \delta _{2-j}=a_{1}\cdot y_{1}+a_{2}\cdot y_{0}+d_{2}=a_{1}\cdot (a_{1}\cdot d_{0}+d_{1})+a_{2}\cdot d_{0}+d_{2}\end{aligned}}}$

Sind diese drei Anfangswerte ${\displaystyle y_{0},\,y_{1}}$ und ${\displaystyle y_{2}}$ als Rekursionsanfang bekannt, so kann man aus diesen Gleichungen direkt die Amplituden ${\displaystyle d_{0},\,d_{1}}$ und ${\displaystyle d_{2}}$ bestimmen:

${\displaystyle {\begin{aligned}d_{0}&=y_{0}\\d_{1}&=y_{1}-a_{1}\cdot d_{0}\\d_{2}&=y_{2}-a_{1}\cdot (a_{1}\cdot d_{0}+d_{1})-a_{2}\cdot d_{0}=y_{2}-a_{1}\cdot (a_{1}\cdot d_{0}+\underbrace {y_{1}-a_{1}\cdot d_{0}} _{d_{1}})-a_{2}\cdot d_{0}=y_{2}-a_{1}\cdot y_{1}-a_{2}\cdot d_{0}\end{aligned}}}$

Im Beispiel der Fibonacci-Zahlen gibt es zwei Anfangsbedingungen ${\displaystyle y_{0}=0}$ und ${\displaystyle y_{1}=1.}$ Die Differenzengleichung wird also mit ${\displaystyle y_{k}=y_{k-1}+y_{k-2}+d_{0}\cdot \delta _{k}+d_{1}\cdot \delta _{k-1},\quad k\geq 0}$ angesetzt. Das heißt, die beiden Koeffizienten ${\displaystyle a_{1}}$ und ${\displaystyle a_{2}}$ sind beide 1, so dass man für die Amplituden der beiden Dirac-Impulse die Werte ${\displaystyle {\begin{aligned}d_{0}&=y_{0}=0\\d_{1}&=y_{1}-a_{1}\cdot d_{0}=1\end{aligned}}}$ und damit die Differenzengleichung ${\displaystyle y_{k}=y_{k-1}+y_{k-2}+\delta _{k-1}}$ erhält.

Lösung der Rekursionsgleichung mittels z-Transformation

Nun kann die gewonnene Differenzengleichung

${\displaystyle y_{k}=\sum _{i=1}^{n}a_{i}\cdot y_{k-i}\quad +\sum _{j=0}^{n-1}d_{j}\cdot \delta _{k-j}}$

mittels z-Transformation gelöst werden. Im ersten Schritt erhält man für die z-Transformierte den Ausdruck

${\displaystyle Y(z)={\mathcal {Z}}\{y_{k}\}=\sum _{i=1}^{n}a_{i}\cdot Y(z)\cdot z^{-i}\quad +\sum _{j=0}^{n-1}d_{j}\cdot 1\cdot z^{-j},}$

in dem man die ${\displaystyle Y(z)}$-Terme auf die linke Seite bringen

${\displaystyle Y(z)\cdot \left(1-\sum _{i=1}^{n}a_{i}\cdot z^{-i}\right)=\sum _{j=0}^{n-1}d_{j}\cdot z^{-j}}$

und anschließend nach ${\displaystyle Y(z)}$ auflösen kann:

${\displaystyle Y(z)={\frac {\sum _{j=0}^{n-1}d_{j}\cdot z^{-j}}{1-\sum _{i=1}^{n}a_{i}\cdot z^{-i}}}}$

bzw. durch Multiplikation mit ${\displaystyle z^{n}}$ im Zähler und Nenner:

${\displaystyle Y(z)={\frac {\sum _{j=0}^{n-1}d_{j}\cdot z^{n-j}}{z^{n}-\sum _{i=1}^{n}a_{i}\cdot z^{n-i}}}}$

Im Allgemeinen erhält man also Polynome gleicher Ordnung im Nenner und im Zähler. Das Zählerpolynom kann nie eine höhere Ordnung als das Nennerpolynom besitzen, weil wie bereits erwähnt, lediglich ${\displaystyle n}$ Anfangswerte vorgegeben werden, so dass die Rekursion beginnen kann. Es kann jedoch vorkommen, dass die Anfangsbedingungen zu Nullwerten bei manchen ${\displaystyle d_{j}}$ Koeffizienten führen, so dass das Zählerpolynom eine kleinere Ordnung als das Nennerpolynom besitzt. Mit diesen Überlegungen kann man also davon ausgehen, dass eine Partialbruchzerlegung möglich ist und die z-Transformierte in Form

${\displaystyle {\begin{aligned}Y(z)&=\sum _{i=1}^{n}{\frac {\alpha _{i}\cdot z+\beta _{i}}{z-p_{i}}}\\&=\sum _{i=1}^{n}\left({\frac {\alpha _{i}\cdot z}{z-p_{i}}}+{\frac {\beta _{i}}{z-p_{i}}}\right)\\&=\sum _{i=1}^{n}\left({\frac {\alpha _{i}\cdot z}{z-p_{i}}}+{\frac {\beta _{i}\cdot z}{z-p_{i}}}\cdot z^{-1}\right)\end{aligned}}}$

geschrieben werden kann. Wegen der Beziehung

${\displaystyle {\mathcal {Z}}\{a^{k}\}={\frac {z}{z-a}}}$

und der Rückwärtsverschiebung (nach rechts) der z-Transformation

${\displaystyle {\mathcal {Z}}\{y_{k-1}\}=z^{-1}\cdot Y(z)}$

erhält man also für die Rücktransformierte

${\displaystyle {\begin{aligned}y_{k}=\sum _{i=1}^{n}\left(\alpha _{i}\cdot p_{i}^{k}+\beta _{i}\cdot p_{i}^{k-1}\right)=\sum _{i=1}^{n}p_{i}^{k-1}\cdot \left(\alpha _{i}\cdot p_{i}+\beta _{i}\right)\end{aligned}}}$

und somit die explizite Formel für die einzelnen Elemente ${\displaystyle y_{k}}$ der rekursiv definierten Zahlenfolge.

Im Beispiel der Fibonacci-Zahlen mit der Differenzengleichung ${\displaystyle y_{k}=y_{k-1}+y_{k-2}+\delta _{k-1}}$ erhält man zunächst durch z-Transformation ${\displaystyle Y(z)=Y(z)\cdot z^{-1}+Y(z)\cdot z^{-2}+1\cdot z^{-1}}$ und daraus ${\displaystyle Y(z)={\frac {z}{z^{2}-z-1}}}$ bzw. mit der Partialbruchzerlegung ${\displaystyle Y(z)={\frac {1}{\sqrt {5}}}\cdot \left({\frac {z}{z-{\frac {1+{\sqrt {5}}}{2}}}}-{\frac {z}{z-{\frac {1-{\sqrt {5}}}{2}}}}\right).}$ Die Rücktransformation ergibt nun direkt die gesuchte explizite Form für die Fibonacci-Zahlenfolge: ${\displaystyle y_{k}={\frac {1}{\sqrt {5}}}\cdot \left(\left({\frac {1+{\sqrt {5}}}{2}}\right)^{k}-\left({\frac {1-{\sqrt {5}}}{2}}\right)^{k}\right).}$ Dass diese „krumme“ Formel tatsächlich ganzzahlige Ergebnisse liefert wird übrigens sofort klar, wenn man die Binomialausdrücke ausschreibt. Wegen des Minuszeichens heben sich die Terme mit geraden Exponenten von ${\displaystyle {\sqrt {5}}}$ auf während die Terme mit ungeraden Exponenten sich addieren und mit dem ${\displaystyle {\sqrt {5}}}$-Term im Nenner kürzen. Damit verbleiben lediglich gerade Exponenten von ${\displaystyle {\sqrt {5}}}$, d. h. Exponenten von 5. Man kann also die obige Gleichung auf mit Fünfer-Potenzen gewichtete Binomialkoeffizienten und das Pascalsche Dreieck zurückführen (siehe detaillierte Herleitung im Artikel Verwandtschaft der Fibonacci-Zahlen mit dem Pascalschen Dreieck).

Siehe auch

• Portal:Mess-, Steuerungs- und Regelungstechnik
• Artikel Regler
• Artikel Digitaler Regler
• 

  Wikibooks: Einführung in die Systemtheorie – Lern- und Lehrmaterialien
• Erzeugende Funktion
• Modifizierte z-Transformation

Literatur

• Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6. 
• Gerd Schulz: Regelungstechnik 2 / Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzy-Regelung. 2. Auflage. Oldenbourg, 2008, ISBN 978-3-486-58318-2. 
• Jan Lunze: Regelungstechnik 2, Mehrgrößensysteme, Digitale Regelung. 7. Auflage. Springer Verlag, 2013, ISBN 978-3-642-10197-7. 
• Alan V. Oppenheim, R. W. Schafer: Zeitdiskrete Signalverarbeitung. Pearson Education, Upper Saddle River, N. J. 2004, ISBN 3-8273-7077-9. 
• Norbert Bischof: Struktur und Bedeutung: Eine Einführung in die Systemtheorie für Psychologen, mit einer Einführung in die Methoden der mathematischen Systemanalyse einschließlich Z-Transformation. 2., korrigierte Auflage. Verlag Hans Huber, Bern 1998, ISBN 3-456-83080-7. 
• Horst Clausert, G. Wiesemann: Grundgebiete der Elektrotechnik, Band 2: Wechselströme, Drehstrom, Leitungen, Anwendungen der Fourier-, der Laplace- und der Z-Transformation. 9. Auflage. Verlag R.Oldenbourg, München 2005, ISBN 3-486-27582-8. 
• N. Fliege: Systemtheorie. Teubner, Stuttgart 1991, ISBN 3-519-06140-6. 

Einzelnachweise

1. ↑ E. R. Kanasewich: Time sequence analysis in geophysics. 3. Auflage. University of Alberta, 1981, ISBN 978-0-88864-074-1, S. 185–186. 
2. ↑ John R. Ragazzini and Lotfi A. Zadeh: The analysis of sampled-data systems. In: Trans. Am. Inst. Elec. Eng. 71. Jahrgang, Nr. II, 1952, S. 225–234. 
3. ↑ Cornelius T. Leondes: Digital control systems implementation and computational techniques. Academic Press, 1996, ISBN 978-0-12-012779-5, S. 123. 
4. ↑ Eliahu Ibrahim Jury: Sampled-Data Control Systems. John Wiley & Sons, 1958. 
5. ↑ Prof. Dr. W. Schuhmacher: Technische Universität Braunschweig, Vorlesungsskript Grundlagen der Regelungstechnik, 309 Seiten, erstellt 6. Oktober 2011, Kapitel: Diskrete Signalverarbeitung durch Digitalrechner.
6. ↑ Oliver Nelles: Zustandsraum und Digitale Regelung. Universität Siegen, 7. Juli 2014, Kapitel: Z-Transformation (Vorlesungsskript, 286 Seiten).
7. ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage, Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6, Kapitel: z-Transformation / Definition der z-Transformation.
8. ↑ Siehe: Gerd Schulz: Regelungstechnik 2. Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzyregelung. 2. Auflage, Oldenbourg Verlag, 2008, Kapitel: Die z-Transformation / Definition.
9. ↑ Oliver Nelles: Zustandsraum und Digitale Regelung. Universität Siegen, 7. Juli 2014, Kapitel: Z-Transformation, S. 232 (Vorlesungsskript, 286 Seiten).
10. ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink, 12. Auflage, Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6, Kapitel: Digitale Regelungssysteme / z-Transformierte der Elementarfunktionen.
11. ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink, 12. Auflage, Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6, Kapitel: z-Übertragungsfunktion (Impulsübertragungsfunktion).
12. ↑ Gerd Schulz: Regelungstechnik 2 Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzyregelung. 2. Auflage, Oldenbourg Verlag, 2008, Kapitel: Diskrete Übertragungsfunktion.
13. ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink, 12. Auflage, Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6, Kapitel: z-Übertragungsfunktion von zeitkontinuierlichen Elementen.
14. ↑ Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink, 12. Auflage, Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6, Kapitel: z-Transformation / z-Übertragungsfunktion von Regelalgorithmen.
15. ↑ Prof. Dr. Ferdinand Svaricek: Universität Bundeswehr München, Vorlesungsskript: 83 Seiten, erstellt April 2012, Kapitel: z-Übertragungsfunktion und Differenzengleichung.
16. ↑ Gerd Schulz: Regelungstechnik 2. Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzy-Regelung. 2. Auflage, Verlag Oldenbourg, 2008, Kapitel: Die z-Transformation.
17. ↑ Siehe: Gerd Schulz: Regelungstechnik 2. Mehrgrößenregelung, Digitale Regelungstechnik, Fuzzyregelung. 2. Auflage, Oldenbourg Verlag, 2008, Hauptkapitel: Diskrete Übertragungsfunktion, Unterkapitel: z-Übertragungsfunktion des Reglers, Berechnungsbeispiel 10.7.