Icke-linjär optimering

Icke-linjär optimering är, inom matematik, optimering av en målfunktion f {\displaystyle f} under förutsättning att vissa bivillkor gäller, och där minst ett av bivillkoren eller målfunktionen är icke-linjär. Detta kan jämföras med linjärprogrammering där alla bivillkor, samt målfunktionen är linjär.

Det generella problemet kan skrivas som:

min x ∈ X f ( x ) {\displaystyle \min _{x\in X}f(x)} , till exempel att man vill minimera en kostnad genom att välja x ur X   {\displaystyle X\ } på rätt sätt

där

f : R n → R {\displaystyle f:R^{n}\to R}
X ⊆ R n . {\displaystyle X\subseteq R^{n}.}

Ofta kan mängden med tillåtna punkter X   {\displaystyle X\ } beskrivas med ett antal bivillkor g i ≤ 0. {\displaystyle g_{i}\leq 0.}

Lösningsmetoder

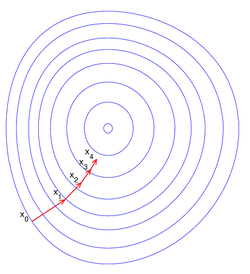
Exempel på ett par iterationer med brantaste lutningmetoden på en funktion med en grop, med nivåkurvor utritade. Man kan även tänka sig en maximering där nivåkurvorna istället beskriver en kulle.

Det finns flera olika lösningsmetoder som beroende på problemets form lämpar sig olika väl. För att ta reda på problemets karaktär är det viktigt att kunna bestämma om problemet är konvext. För detta gäller att målfunktionen ska vara konvex på den tillåtna mängden X   {\displaystyle X\ } som också måste vara konvexa.

Om problemet inte är konvext så är det vanligt att någon typ av relaxation görs för att få ett konvext problem, för vilka bra lösningsmetoder finns. Det är även vanligt att man relaxerar genom att häva ett av villkoren och istället bildar en straffunktion med det hävda villkoret.

Allmän iterativ sökning av lokalt minimum

Praktiskt använder man en iterativ sökmetod för att hitta ett lokalt optimum (i detta fall minimum)

  1. välj startpunkt x 0 , sätt  k = 0   {\displaystyle x^{0}{\mbox{, sätt }}k=0\ }
  2. välj sökriktning d k ≠ 0 {\displaystyle d^{k}\neq 0}
  3. bestäm steglängd t k   {\displaystyle t_{k}\ } genom att lösa det endimensionella problemet min t ≥ 0 φ ( t ) = f ( x k + t d k ) {\displaystyle \min _{t\geq 0}\varphi (t)=f(x^{k}+td^{k})}
  4. ny iterationspunkt x k + 1 = x k + t k d k   {\displaystyle x^{k+1}=x^{k}+t_{k}d^{k}\ }
  5. sätt k = k + 1   {\displaystyle k=k+1\ } och upprepa tills avbrottskriterium uppfylls

Val av sökriktning

Om problemet är att minimera f, så väljs riktningen d k   {\displaystyle d^{k}\ } så att f minskar i denna riktning, d k   {\displaystyle d^{k}\ } kallas då avtaganderiktning eller descentriktning. Detta villkor på d k   {\displaystyle d^{k}\ } kan skrivas:

∇ f ( x ) T d k < 0 {\displaystyle \nabla f(x)^{T}d^{k}<0} ty då är vinkeln mellan f:s gradient och riktningen d k   {\displaystyle d^{k}\ } större än 90 grader.

Om d k   {\displaystyle d^{k}\ } väljs parallell med den negativa gradienten till f så erhålls brantaste lutningmetoden (BL), eftersom gradienten pekar i den riktning var i funktionen ökar snabbat. Denna metod kan dock ge väldigt många iterationer med korta steg för att sedan börja ta längre steg igen, typiskt sker detta nere i ett "dike" eller uppe på en "ås". En annan metod som är bättre men kräver mer beräkning (dyrare) än BL, är Newtons metod där riktningen väljs som

d k = − ∇ 2 f ( x k ) − 1 ∇ f ( x k ) {\displaystyle d^{k}=-\nabla ^{2}f(x^{k})^{-1}\nabla f(x^{k})}

Den riktning kan fås med följande beräkning

  • approximera f i iterationspunkten x k {\displaystyle x^{k}} med en andra ordningens Taylorutveckling:
    q ( x ) = f ( x k ) + ∇ f ( x k ) T ( x − x k ) + 1 2 ( x − x k ) ∇ 2 f ( x k ) ( x − x k ) {\displaystyle q(x)=f(x^{k})+\nabla f(x^{k})^{T}(x-x^{k})+{1 \over 2}(x-x^{k})\nabla ^{2}f(x^{k})(x-x^{k})}
  • sök stationärpunkt, x ¯ k {\displaystyle {\bar {x}}^{k}} , till q ( x ) {\displaystyle q(x)}
    ∇ q ( x ) = ∇ f ( x k ) + ∇ 2 f ( x k ) ( x − x k ) = 0 ⇒ − ∇ 2 f ( x k ) − 1 ∇ f ( x k ) = x ¯ k − x k {\displaystyle \nabla q(x)=\nabla f(x^{k})+\nabla ^{2}f(x^{k})(x-x^{k})=0\Rightarrow -\nabla ^{2}f(x^{k})^{-1}\nabla f(x^{k})={\bar {x}}^{k}-x^{k}} , som är riktningen från x k   {\displaystyle x^{k}\ } till x ¯ k {\displaystyle {\bar {x}}^{k}}

Val av steglängd

Generellt kan det vara nästan omöjligt att finna ett globalt optimalt steg (globalt minimum till φ ( t ) {\displaystyle \varphi (t)} ) och därför nöjer man sig ofta med att hitta ett lokalt optimalt steg. Ett lokalt optimalt steg kan resultera i en punkt som är sämre än den nuvarande punkten.

Vid begränsat problem

Då man har ett problem som är begränsat så är det inte säkert att alla avtagande riktningar är tillåtna, de kan peka ut i det otillåtna området så att man skulle kunna hamna utanför X   {\displaystyle X\ } om man tar ett (för långt) steg i den riktningen. Om det finns ett tillräckligt litet steg t > 0 {\displaystyle t>0} sådant att man fortfarande befinner i sig i den tillåtna mängden x ¯ + t d k ∈ X {\displaystyle {\bar {x}}+td^{k}\in X} så är riktningen d k ≠ 0 {\displaystyle d^{k}\neq 0} en tillåten riktning från x ¯ {\displaystyle {\bar {x}}} .

Om det inte finns någon tillåten avtaganderiktning från den punkt där man står, så befinner man sig redan i ett lokalt minimum. Annars skulle man kunna ta ett steg i den tillåtna avtaganderiktningen och erhålla ett lägre bättre värde på funktionen f.

Källor

  • Jan Lundgren, Mikael Rönnqvist och Peter Värbrand (2003). Optimeringslära. Studentlitteratur