Charakterystyka Eulera

Charakterystyka Eulera, charakterystyka Eulera-Poincarégo^[1][2] – niezmiennik topologiczny^[3] początkowo definiowany jedynie dla wielościanów wypukłych.

Powierzchnie wielościanów wypukłych

Wprowadźmy oznaczenia:

• ${\displaystyle W}$ – liczba wierzchołków,
• ${\displaystyle S}$ – liczba ścian,
• ${\displaystyle K}$ – liczba krawędzi.

Charakterystykę Eulera, oznaczaną tradycyjnie literą ${\displaystyle \chi ,}$ dla powierzchni wielościanów wypukłych definiuje się jako^[2]:

${\displaystyle \chi =W-K+S.}$

Wielościany wypukłe spełniają twierdzenie Eulera o wielościanach, co oznacza, że zachodzi wzór:

${\displaystyle W+S=K+2.}$

Charakterystyka Eulera powierzchni wielościanów wypukłych wynosi zatem ${\displaystyle 2.}$

Własność ta została po raz pierwszy zauważona^[4] (jedynie dla brył platońskich) w 1537 roku przez Francesco Maurolico w jego nieopublikowanym manuskrypcie. Następnie, dla wielościanów wypukłych własność tę zauważył Euler. Pierwszy poprawny dowód jej prawdziwości podał Legendre^[5].

Wielościany dowolne

Ta sama definicja (czyli ${\displaystyle \chi =W-K+S}$) obowiązuje także dla innych wielościanów. Każda powierzchnia wielościanu homeomorficzna z powierzchnią wielościanu wypukłego ma charakterystykę równą 2. Nie jest to prawdą dla wszystkich powierzchni wielościanów: wszystkie powierzchnie wielościanów homeomorficzne z torusem (czyli takie, przez środek których „przechodzi dokładnie jedna dziura”) mają charakterystykę równą 0.

Definicja ogólna

Niech ${\displaystyle X}$ będzie przestrzenią topologiczną. Jej charakterystykę Eulera definiujemy jako^[6]

${\displaystyle \chi (X)=\sum _{i=0}^{\infty }(-1)^{i}{\text{rank}}(H_{i}(X)),}$

gdzie ${\displaystyle {\text{rank}}(H_{i}(X))}$ jest rangą ${\displaystyle i}$-tej grupy homologii (tj. ${\displaystyle i}$-tą liczbą Bettiego) przestrzeni ${\displaystyle X.}$ Definicja ta ma sens jedynie wtedy, gdy wszystkie liczby Bettiego oraz ich suma są skończone.

W przypadku, gdy ${\displaystyle X}$ jest skończonym CW-kompleksem, to jego charakterystyka Eulera jest równa

${\displaystyle \chi (X)=\sum _{i=0}^{\infty }(-1)^{i}k_{i},}$

gdzie ${\displaystyle k_{i}}$ oznacza liczbę komórek wymiaru ${\displaystyle i.}$ W szczególności, w przypadku kompleksów symplicjalnych ${\displaystyle k_{i}}$ oznacza liczbę ${\displaystyle i}$-wymiarowych sympleksów.

Powierzchnie

Aby obliczyć charakterystykę Eulera powierzchni (jak i innych, wyżej wymiarowych wielościanów) wystarczy znaleźć jej rozkład komórkowy. Np. dla sfery wystarczy jedna komórka 0-wymiarowa oraz jedna wymiaru 2. Przedstawienie sfery w postaci wielościanu wymaga co najmniej 4 ścian, 4 wierzchołków oraz 6 krawędzi.

Nazwa powierzchni	Wygląd	Charakterystyka Eulera
Sfera		2
Torus		0
Wstęga Möbiusa (z brzegiem)		0
Butelka Kleina		0
Płaszczyzna rzutowa rzeczywista		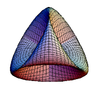1
Dwie sfery (niepołączone)		2 + 2 = 4
${\displaystyle n}$ niepołączonych sfer		${\displaystyle 2n}$

Uogólnienia

• Jeżeli ${\displaystyle X}$ jest skończonym wielościanem, to ${\displaystyle \chi (X)}$ jest równa liczbie Lefschetza identyczności^[6] ${\displaystyle {\text{id}}_{X}.}$
• Niech ${\displaystyle {\mathcal {C}}}$ będzie skończoną kategorią. Tj. taką, że liczba morfizmów (a więc i obiektów) jest skończona. Oznaczmy przez ${\displaystyle A_{1},\dots ,A_{n}}$ jej obiekty. Z taką kategorią możemy stowarzyszyć macierz ${\displaystyle M_{\mathcal {C}}}$ wymiaru ${\displaystyle n\times n,}$ gdzie ${\displaystyle m_{ij}}$ jest liczbą morfizmów ${\displaystyle A_{i}\to A_{j}.}$ Jeżeli istnieją takie ${\displaystyle [x^{1},\dots ,x^{n}],[x_{1},\dots ,x_{n}]\in \mathbb {Q} ^{n},}$ że

${\displaystyle M_{\mathcal {C}}{\begin{bmatrix}x^{1}\\x^{2}\\\dots \\x^{n}\end{bmatrix}}={\begin{bmatrix}1\\1\\\dots \\1\end{bmatrix}}{\text{ oraz }}{\begin{bmatrix}x_{1}&x_{2}&\dots &x_{n}\end{bmatrix}}M_{\mathcal {C}}={\begin{bmatrix}1&1&\dots &1\end{bmatrix}},}$ to ${\displaystyle \sum _{i=1}^{n}x^{i}=\sum _{i=1}^{n}x_{i}.}$

Powyższą sumę nazywamy charakterystyką Eulera kategorii ${\displaystyle {\mathcal {C}}.}$ Jest ona liczbą wymierną. Jeżeli przestrzeń klasyfikująca kategorii ${\displaystyle {\mathcal {C}}}$ jest skończonym wielościanem, to jego charakterystyka Eulera jest równa^[7] ${\displaystyle \chi ({\mathcal {C}}).}$

Aksjomatyzacja

Charakterystykę Eulera można zdefiniować również aksjomatycznie. Dokładniej, zredukowana charakterystyka Eulera (tj. charakterystyka minus 1) jest jedyną^[8][9] całkowitoliczbową funkcją ${\displaystyle \epsilon }$ określoną na zbiorze klas homeomorfizmów skończonych wielościanów (z punktem bazowym) spełniającą warunki:

(1)${\displaystyle \epsilon (X)=\epsilon (A)+\epsilon (X/A),}$

(2)${\displaystyle \epsilon (\mathbb {S} ^{0})=1,}$

dla dowolnej pary wielościanów ${\displaystyle A\subseteq W.}$

Zobacz też

• genus, niezmiennik powiązany z Ch. Eulera
• krzywizna Gaussa

Przypisy

Linki zewnętrzne

• Eric W.E.W. Weisstein Eric W.E.W., Polyhedral Formula, [w:] MathWorld, Wolfram Research  (ang.). [dostęp 2023-06-18].