Ślimak Teodorosa

Ślimak Teodorosa

Ślimak Teodorosa, spirala Teodorosa – konstrukcja geometryczna, pozwalająca stworzyć odcinek o długości równej pierwiastkowi z danej liczby naturalnej[1]. Zasada konstrukcji opiera się na twierdzeniu Pitagorasa. Nazwa konstrukcji pochodzi od imienia greckiego matematyka i filozofa, Teodorosa z Cyreny. Autorem konstrukcji był Jakob Heinrich Anderhub, matematyk amator, który opisał ją w pracy Joco-Seria, aus den Papieren eines reisenden Kaufmanns z 1941 roku[2].

Opis konstrukcji

  1. Budujemy trójkąt prostokątny o przyprostokątnych długości 1. Przeciwprostokątna trójkąta ma długość 2 . {\displaystyle {\sqrt {2}}.}
  2. Konstruujemy kolejny trójkąt prostokątny, którego jedną przyprostokątną jest przeciwprostokątna trójkąta z pkt. 1, a druga przyprostokątna ma długość 1. Przeciwprostokątna otrzymanego trójkąta ma długość 3 . {\displaystyle {\sqrt {3}}.}
  3. Czynność tę powtarzamy, tworząc kolejne trójkąty prostokątne. Za każdym razem jedna z przyprostokątnych jest zarazem przeciwprostokątną trójkąta z poprzedniego kroku, a druga ma długość 1. Długości przeciwprostokątnych są pierwiastkami kolejnych liczb naturalnych.

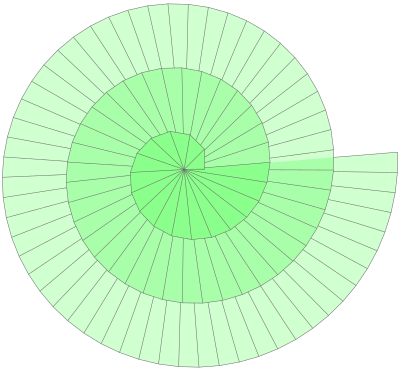
Konstrukcja w 17 kroku prowadzi do nakładania się trójkątów na siebie[1], jak na ilustracji obok. Jeśli będzie kontynuowana, trzecia grupa trójkątów podwójnie nakładających się na siebie nastąpi w 54. kroku itd.

Najprostsze własności

n {\displaystyle n} -ty trójkąt konstrukcji

Niech φ n {\displaystyle \varphi _{n}} oznacza kąt ostry n {\displaystyle n} -tego trójkąta o wierzchołku w środku całej konstrukcji. Wówczas:

tg ⁡ φ n = 1 n . {\displaystyle \operatorname {tg} \varphi _{n}={\frac {1}{\sqrt {n}}}.}

Stąd oczywiście:

φ n = arctg ⁡ 1 n . {\displaystyle \varphi _{n}=\operatorname {arctg} {\frac {1}{\sqrt {n}}}.}

Suma

∑ k = 1 n φ k {\displaystyle \sum _{k=1}^{n}\varphi _{k}}

wyznacza kąt dla przeciwprostokątnej n {\displaystyle n} -tego trójkąta o długości n + 1 {\displaystyle {\sqrt {n+1}}} względem przyprostokątnej o długości 1 {\displaystyle {\sqrt {1}}} 1-go trójkąta poprowadzonej ze środka konstrukcji.

W 1958 roku Erich Teuffel udowodnił, że żadne dwie przeciwprostokątne nie pokryją się, tzn.

∑ k = 1 n 1 φ k ≠ ∑ k = 1 n 2 φ k {\displaystyle \sum _{k=1}^{n_{1}}\varphi _{k}\neq \sum _{k=1}^{n_{2}}\varphi _{k}} dla n 1 ≠ n 2 {\displaystyle n_{1}\neq n_{2}} [3].

Historia

Rozszerzony ślimak Teodorosa.

Konstrukcja zwana ślimakiem Teodorosa była niekiedy przypisywana Teodorosowi jako stosowana przez niego metoda wyznaczania odcinka o długości proporcjonalnej do pierwiastka kwadratowego z całkowitej wielokrotności danego odcinka jednostkowego. W rzeczywistości pitagorejczycy, którzy opracowali i rozwinęli metodę kwadratury wielokątów, potrafili „pierwiastkować” odcinki o dowolnej rzeczywistej nieujemnej długości. Np. kwadratura dowolnego trójkąta o podstawie 2 i wysokości h {\displaystyle h} prowadziła „w jednym kroku” do konstrukcji kwadratu o boku h   ( h ∈ R + ) , {\displaystyle {\sqrt {h}}\ (h\in R^{+}),} podczas gdy metoda użyta w ślimaku Teodorosa jest niepraktyczna i żmudna – wyznaczenie odcinka długości n   ( n ∈ N ) {\displaystyle {\sqrt {n}}\ (n\in N)} wymaga n {\displaystyle n} -krotnego powtórzenia każdego kroku konstrukcji.

Ślimak Teodorosa jest znany głównie dzięki fragmentowi dialogu Platona Teajtet[4] będącego relacją z badań Teodorosa nad niewymiernością boków kwadratów o danych całkowitych polach[5].

Wzmianka o siedemnastostopowym kwadracie w zdaniu

...i tak po jednym każdy kwadrat brał pod uwagę aż do siedemnastostopowego; na tym się jakoś zatrzymał.
Platon Parmenides. Teajtet, przeł. Władysław Witwicki. Kęty: Wydawnictwo Antyk, 2002, s. 99.

wywoływała wiele domysłów i spekulacji próbujących znaleźć przyczynę zatrzymania się Teodorosa w swoich badaniach właśnie na kwadracie o polu 17[2].

Przez zbieżność tej siedemnastki z siedemnastym krokiem konstrukcji ślimaka Teodorosa, w którym trójkąt nakłada się na pierwszy już narysowany, konstrukcja ta była traktowana jako jedno z możliwych wyjaśnień tego fragmentu z Platona.

Funkcja Teodorosa i stała Teodorosa

Linia łamana, utworzona przez krótsze przyprostokątne opisanych wyżej trójkątów prostokątnych (przyprostokątne o długości 1), bywa niekiedy nazywana dyskretną spiralą Teodorosa[6]. Philip Davis określił położenie wierzchołków tej spirali na płaszczyźnie zespolonej poprzez równanie rekurencyjne[7]:

z 0 = 1 , z n + 1 = z n + i z n | z n | , {\displaystyle z_{0}=1,\;\;z_{n+1}=z_{n}+i{\frac {z_{n}}{|z_{n}|}},}

gdzie i {\displaystyle i} jest jednostką urojoną, | z | {\displaystyle |z|} oznacza moduł liczby zespolonej z . {\displaystyle z.}

Wzór

| z n | = n + 1 {\displaystyle |z_{n}|={\sqrt {n+1}}}

łatwo można wykazać indukcyjnie, bo | z 0 | = 1 = 1 {\displaystyle |z_{0}|={\sqrt {1}}=1} oraz

| z n | = | z n − 1 + i z n − 1 | z n − 1 | | = | z n − 1 | ⋅ | 1 + i | z n − 1 | | = ∗ n ⋅ | 1 + i n | = | n + i | = n + 1 , {\displaystyle |z_{n}|=\left|z_{n-1}+{\frac {iz_{n-1}}{|z_{n-1}|}}\right|=|z_{n-1}|\cdot \left|1+{\frac {i}{|z_{n-1}|}}\right|\,{\stackrel {*}{=}}\,{\sqrt {n}}\cdot \left|1+{\frac {i}{\sqrt {n}}}\right|=|{\sqrt {n}}+i|={\sqrt {n+1}},}

w miejscu oznaczonym gwiazdką (*) wykorzystano założenie indukcyjne | z n − 1 | = n . {\displaystyle |z_{n-1}|={\sqrt {n}}.}

Korzystając z powyższej własności, Davis przekształcił wzór rekurencyjny w postaci iteracyjnej[7]

z n = ∏ k = 1 n ( 1 + i k ) . {\displaystyle z_{n}=\prod _{k=1}^{n}\left(1+{\frac {i}{\sqrt {k}}}\right).}

Zagadnienie, jak zinterpolować wierzchołki dyskretnej spirali Teodorusa za pomocą krzywej gładkiej, postawił i rozwiązał Davis[8], wykorzystując analogię z wzorem Eulera dla funkcji gamma jako rozszerzenia silni. Jako rozwiązanie zagadnienia przedstawił wzór:

T ( x ) = ∏ k = 1 ∞ 1 + i k 1 + i k + x , {\displaystyle T(x)=\prod _{k=1}^{\infty }{\frac {1+{\frac {i}{\sqrt {k}}}}{1+{\frac {i}{\sqrt {k+x}}}}},}

wykazał jego zbieżność dla x > − 1 {\displaystyle x>-1} i zaproponował dla niego nazwę funkcja Teodorosa.

Stałą Teodorosa T {\displaystyle T} nazwał Davis nachylenie (gradient) funkcji Teodorosa w punkcie ( 0 , 0 ) {\displaystyle (0,0)} [a][9]:

T = ∑ k = 1 ∞ 1 ( k + 1 ) k = ∑ k = 1 ∞ 1 k 3 / 2 + k 1 / 2 = 1 2 − ∑ k = 1 ∞ ( − 1 ) k [ ζ ( k + 1 2 ) − 1 ] = 1,860 0250... , {\displaystyle {\begin{aligned}T&=\sum _{k=1}^{\infty }{\frac {1}{(k+1){\sqrt {k}}}}\\&=\sum _{k=1}^{\infty }{\frac {1}{k^{3/2}+k^{1/2}}}\\&={\frac {1}{2}}-\sum _{k=1}^{\infty }(-1)^{k}[\,\zeta (k+{\frac {1}{2}})-1\,]\\&=1{,}8600250...,\end{aligned}}}

gdzie ζ ( z ) {\displaystyle \zeta (z)} jest funkcją dzeta Riemanna.

Stosując zaawansowane metody analityczne i numeryczne, stałą Teodorosa do 50. miejsca po przecinku obliczył Walter Gautschi[10][11].

Uwagi

  1. ↑ Stałą Teodorosa bywa także nazywana wartość 3 . {\displaystyle {\sqrt {3}}.}

Przypisy

  1. ↑ a b Mateusz Majka: Ślimak Teodorosa. zobaczycmatematyke.krk.pl. [dostęp 2017-07-13]. (pol.).
  2. ↑ a b Davis 1993 ↓, s. 7–8.
  3. ↑ Erich Teuffel. Eine Eigenschaft der Quadratwurzelschnecke. „Math.-Phys. Semesterber.”. 6, s. 148–152, 1958. 
  4. ↑ J.J. O’Connor, E.F. Robertson: Theodorus of Cyrene. MacTutor History of Mathematics. [dostęp 2017-07-24]. (ang.).
  5. ↑ Kwestię tę dokładnie wyjaśniają Jean Itard, Les livres arithmétiques d’Euclide, s. 33–39, Hermann, Paris 1961 oraz Wilbur R. Knorr, The evolution of the Euclidean Elements, Reidel, Dordrecht-Boston 1975, s. 62–108.
  6. ↑ Eric W.E.W. Weisstein Eric W.E.W., Theodorus Spiral, [w:] MathWorld, Wolfram Research [dostęp 2017-07-24]  (ang.).
  7. ↑ a b Davis 1993 ↓, s. 33–34.
  8. ↑ Davis 1993 ↓, s. 38.
  9. ↑ Eric W.E.W. Weisstein Eric W.E.W., Theodorus’s Constant, [w:] MathWorld, Wolfram Research [dostęp 2017-07-27]  (ang.).
  10. ↑ Davis 1993 ↓, s. 67–87.
  11. ↑ Walter Gautschi: The Spiral of Theodorus, Numerical Analysis, and Special Functions. Purdue University, Department of Computer Science. [dostęp 2017-07-27].

Bibliografia

  • Philip J. Davis: Spirals. From Theodorus to Chaos. Wellesley: A. K. Peters, 1993. ISBN 1-56881-010-5.

Linki zewnętrzne

  • Konstrukcja ślimaka Teodorosa. blogiceo.nq.pl. [dostęp 2017-07-13]. [zarchiwizowane z tego adresu (2011-05-04)]. (pol.).
  • Eric W.E.W. Weisstein Eric W.E.W., Theodorus Spiral, [w:] MathWorld, Wolfram Research [dostęp 2017-07-24]  (ang.).


Zobacz multimedia związane z tematem: Ślimak Teodorosa