Sinussetning

Sinussetningen (også kalt sinusproporsjonen) er i trigonometrien (se også trigonometriske funksjoner) en læresetning om en hvilken som helst trekant i planet. Når a, b, og c er sidene i trekanten, og disse sidenes motstående vinkler er A, B og C, sier sinussetningen at

${\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}.}$

Den felles verdien av disse tre brøkene er diameteren til trekantens omskrevne sirkel. Sinussetningen kan også fremstilles som

${\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}.}$

Denne setningen er nyttig når man skal beregne resten av sidene i en trekant der to vinkler og en side er kjent, et kjent problem i triangulering. Den kan også brukes når to sider og en vinkel som ikke ligger mellom dem, er kjent; i noen tilfeller gir formelen to mulige verdier for den mellomliggende vinkelen. Når det skjer, vil ofte bare ett resultat få vinkelsummen til å bli 180°; i andre tilfeller har trekanten to løsninger.

Det kan vises at diameteren til trekantens omskrevne sirkel er

${\displaystyle {\begin{aligned}{\frac {abc}{2S}}&{}={\frac {abc}{2{\sqrt {s(s-a)(s-b)(s-c)}}}}\\&{}={\frac {2abc}{\sqrt {(a^{2}+b^{2}+c^{2})^{2}-2(a^{4}+b^{4}+c^{4})}}},\end{aligned}}}$

der S er trekantens areal og s dens halve omkrets

${\displaystyle s={\frac {a+b+c}{2}}.}$

Eksempler

Gitt en trekant med side a = 20, side c = 24, og vinkel C = 40°

Ved å bruke sinussetningen kommer vi frem til at

${\displaystyle {\frac {\sin A}{20}}={\frac {\sin 40^{\circ }}{24}}.}$

${\displaystyle A=\arcsin \left({\frac {20\sin 40^{\circ }}{24}}\right)\cong 32,39^{\circ }.}$

Et annet eksempel på å løse et problem ved hjelp av sinussetningen:

Hvis de to sidene i en trekant er lik R og lengden av den tredje siden, korden, er gitt som 100 meter, og vinkel C motstående korden er gitt i grader, er

${\displaystyle \angle A=\angle B={\frac {180-C}{2}}}$

og

${\displaystyle {R \over \sin A}={{\mbox{korde}} \over \sin C}{\text{ eller }}{R \over \sin B}={{\mbox{korde}} \over \sin C}\,}$

${\displaystyle {{\mbox{korde}}\,\sin A \over \sin C}=R{\text{ eller }}{{\mbox{korde}}\,\sin B \over \sin C}=R.}$

Utledning

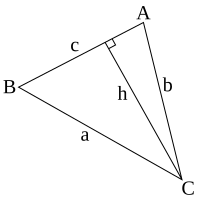
Lag en trekant med sider a, b og c, og vinkler A, B og C. Tegn høyden fra vinkel C til side c; per definisjon vil den dele den opprinnelige trekanten i to rettvinklede trekanter. Kall høyden h.

Vi ser at

${\displaystyle \sin A={\frac {h}{b}}{\text{ and }}\sin B={\frac {h}{a}}.}$

Derfor er

${\displaystyle h=b\,(\sin A)=a\,(\sin B)}$

og

${\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}.}$

Ved å gjøre det samme med høyden fra A får vi

${\displaystyle {\frac {b}{\sin B}}={\frac {c}{\sin C}}.}$

Se også

• Sinus