Scheidingsaxioma

Dit artikel gaat over eigenschappen van topologische ruimten in de wiskunde. Zie axiomaschema van afscheiding voor het begrip uit de verzamelingenleer.

Aan een topologische ruimte worden soms aanvullende voorwaarden opgelegd om de ruimte sterkere eigenschappen te geven. De scheidingsaxioma's zijn dergelijke voorwaarden, die alle te maken hebben met de mogelijkheid of onmogelijkheid, verschillende elementen van de ruimte te onderscheiden door middel van open verzamelingen. De axioma's worden traditioneel aangeduid met de letter ${\displaystyle T}$, van het Duitse woord voor scheiding: 'Trennung'. De axioma's zijn geïndiceerd met de getallen 0, 1, 2, etc.. waarbij een hogere index een sterkere voorwaarde betekent. Er zijn inmiddels ook halftallige indices, om aan te geven dat het axioma wat sterkte betreft ligt tussen de beide axioma's met naastliggende indices.

In de onderstaande opsomming staan de scheidingsaxioma's vermeld in de vorm van de eis of eisen die aan de bijbehorende ruimte gesteld wordt resp. worden.

T₀: Kolmogorov-ruimte

Een topologische ruimte heet een Kolmogorov-ruimte, ook ${\displaystyle T_{0}}$-ruimte of kortweg ${\displaystyle T_{0}}$, als bij ieder paar punten een open verzameling bestaat die precies een van de twee punten bevat. Met andere woorden: alle punten kunnen van elkaar worden gescheiden door open verzamelingen.

De meeste praktische, elementaire voorbeelden van topologische ruimten zijn ${\displaystyle T_{0}}$, dus het is interessanter een tegenvoorbeeld te geven. De indiscrete topologie op een verzameling ${\displaystyle X}$ heeft slechts twee open verzamelingen: de lege verzameling en ${\displaystyle X}$ zelf. Als ${\displaystyle X}$ minstens twee elementen bevat, dan is de indiscrete topologie niet ${\displaystyle T_{0}}$.

Een pseudometrische ruimte die geen metrische ruimte is, geeft aanleiding tot een topologie die niet ${\displaystyle T_{0}}$ is. Twee verschillende punten met onderlinge afstand 0 kunnen immers niet gescheiden worden door open verzamelingen.

T₁: Fréchet-ruimte

Een topologische ruimte heet Fréchet-ruimte, ook ${\displaystyle T_{1}}$-ruimte of kortweg ${\displaystyle T_{1}}$, als voor ieder paar punten ${\displaystyle x}$ en ${\displaystyle y}$ een open verzameling bestaat die ${\displaystyle x}$ bevat maar niet ${\displaystyle y}$, en een open verzameling die ${\displaystyle y}$ bevat maar niet ${\displaystyle x}$. Dit is gelijkwaardig met de eis dat alle singletons gesloten verzamelingen zijn.

Het is gemakkelijk te zien dat ${\displaystyle T_{1}}$ minstens even sterk is als ${\displaystyle T_{0}}$: elke ${\displaystyle T_{1}}$-ruimte is een ${\displaystyle T_{0}}$-ruimte. Het omgekeerde is niet waar: er zijn ${\displaystyle T_{0}}$-ruimten die niet ${\displaystyle T_{1}}$ zijn.

Een niet-triviaal voorbeeld van dit laatste vormt de Zariski-topologie op het spectrum van een commutatieve ring (zie de voorbeelden bij de definitie van een topologische ruimte). Deze is altijd ${\displaystyle T_{0}}$, maar ze is pas ${\displaystyle T_{1}}$ als alle priemidealen van de ring maximaal zijn.

T₂: Hausdorff-ruimte

Een topologische ruimte heet Hausdorff-ruimte, ook ${\displaystyle T_{2}}$-ruimte of kortweg ${\displaystyle T_{2}}$, als voor ieder paar punten ${\displaystyle x}$ en ${\displaystyle y}$ disjuncte open verzamelingen ${\displaystyle F}$ en ${\displaystyle G}$ bestaan zodat elk van beide open verzamelingen precies een van de twee punten bevat. Dit is gelijkwaardig met de eis dat de diagonaalverzameling ${\displaystyle \{(x,x)|x\in X\}}$ een gesloten deel is in de producttopologie van het Cartesisch product ${\displaystyle X\times X}$.

Het is opnieuw gemakkelijk te zien dat ${\displaystyle T_{2}}$ minstens even sterk is als ${\displaystyle T_{1}}$. En ook hier bestaan er tegenvoorbeelden voor de omgekeerde bewering. De cofiniete topologie (zie voorbeelden topologische ruimte) is altijd ${\displaystyle T_{1}}$, maar ze is slechts ${\displaystyle T_{2}}$ op een eindige ruimte.

T₃: reguliere ruimte

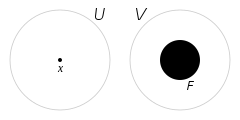
Een topologische ruimte heet regulier, ook ${\displaystyle T_{3}}$-ruimte of kortweg ${\displaystyle T_{3}}$, als aan de volgende twee voorwaarden voldaan is:

1. de ruimte is ${\displaystyle T_{1}}$
2. voor elk punt ${\displaystyle x}$ en elke gesloten verzameling ${\displaystyle F}$ en die ${\displaystyle x}$ niet bevat, bestaat er een paar disjuncte open verzamelingen ${\displaystyle U}$ en ${\displaystyle V}$ zodanig dat ${\displaystyle x}$ tot ${\displaystyle U}$ en ${\displaystyle F}$ een deel is van ${\displaystyle V}$.

Als een ruimte ${\displaystyle T_{3}}$ is, dan is ze ook ${\displaystyle T_{2}}$. Immers, uit de eerste voorwaarde volgt dat alle singletons gesloten zijn. Maar door de tweede voorwaarde toe te passen op het bijzondere geval van de gesloten verzameling]${\displaystyle F=\{y\}}$ volgt de voorwaarde ${\displaystyle T_{2}}$.

Er bestaan voorbeelden van niet-reguliere Hausdorff-ruimten.

T₄: normale ruimte

Een topologische ruimte heet normaal, ook ${\displaystyle T_{4}}$-ruimte of kortweg ${\displaystyle T_{4}}$, als aan de volgende twee voorwaarden voldaan is:

1. de ruimte is ${\displaystyle T_{1}}$
2. voor elk paar disjuncte gesloten verzamelingen ${\displaystyle E}$ en ${\displaystyle F}$ bestaan er disjuncte open verzamelingen ${\displaystyle U}$ en ${\displaystyle V}$ zodanig dat ${\displaystyle E}$ een deel is van ${\displaystyle U}$, en ${\displaystyle F}$ een deel is van ${\displaystyle V}$.

Elke ${\displaystyle T_{4}}$-ruimte is ook ${\displaystyle T_{3}}$. Immers, de eerste voorwaarde is in beide gevallen identiek. En uit de eerste voorwaarde volgt dat alle singletons gesloten zijn. Maar door de tweede voorwaarde toe te passen op het bijzondere geval van de gesloten verzameling ${\displaystyle E=\{x\}}$ volgt de tweede ${\displaystyle T_{3}}$-voorwaarde.

Er bestaan voorbeelden van niet-normale, reguliere ruimten.

T_3½

Pavel Urysohn bewees dat in een normale ruimte steeds de volgende stelling geldt: voor ieder punt ${\displaystyle x}$ en voor iedere gesloten verzameling ${\displaystyle G}$ waar ${\displaystyle x}$ niet toe behoort, bestaat er een continue afbeelding van de hele ruimte ${\displaystyle X}$ naar het gesloten interval ${\displaystyle [0,1]}$ die ${\displaystyle x}$ afbeeldt op ${\displaystyle 0}$, en ${\displaystyle G}$ op ${\displaystyle {1}}$.

Niet alle ruimten waarin bovenstaande stelling geldt, zijn normaal. We noemen dergelijke ruimten Tychonov-ruimten of volledige, reguliere ruimten. Niet alle auteurs hanteren dezelfde benamingen. Er zijn auteurs die voor een volledige, reguliere ruimte niet het Hausdorff-axioma (${\displaystyle T_{2}}$) eisen, en onder een Tychonov-ruimte een volledige, reguliere Hausdorff-ruimte verstaan.

De benaming ${\displaystyle T_{3{\frac {1}{2}}}}$ voor deze ruimten volgt uit het feit (niet moeilijk te bewijzen) dat elke Tychonov-ruimte regulier is, dus ${\displaystyle T_{3{\frac {1}{2}}}}$ is minstens even sterk als ${\displaystyle T_{3}}$.

Metrische ruimten zijn normaal, en voldoen dus meteen aan alle scheidingsaxioma's. Niet alle normale topologische ruimten kunnen verkregen worden uit een metriek; om metriseerbaarheid te garanderen moeten ook aftelbaarheidseigenschappen voldaan zijn (zie aftelbaarheidsaxioma's).