白銀比

縦と横の長さの比が 1 : √2, 1 : (1 + √2) の長方形における性質。左上の頂点から右上がりの対角線に垂線を引き、その交点を第1交点とする。その垂線が下底に反射したときの直線と右上がりの対角線の交点を第2交点とする。
1 : √2 の場合は、第1交点と第2交点が縦横共に3等分できる位置にある。
1 : (1 + √2) の場合は、第2交点が、左下の頂点との距離が1で、左下の角の2等分線上にある。

白銀比（はくぎんひ）と呼ばれるものは以下の2つがあり、いずれも無理比である。

  1. 比 1 : ( 1 + 2 ) {\displaystyle 1:(1+{\sqrt {2}})} のこと。貴金属比の一つ（第2貴金属比）。
  2. 比 1 : 2 {\textstyle 1:{\sqrt {2}}} のこと。b/2 : a = a : bを満たす比であることから、紙の寸法などに用いられている。

1 : (1+ √2) の白銀比

1 : (1+ √2) の白銀長方形
幾何学的に、正円とその中心を通る水平並びに傾き１の直線を利用すると、 図のように「1 : (1+ √2)」の白銀長方形を描ける。

1 : (1+ √2) の白銀比（はくぎんひ、英語: silver ratio / silver mean / silver constant）は、貴金属比の一つ（第2貴金属比）である[1]。近似値は 1 : 2.414 である。英語でsilver ratioなどと言った場合はこちらを指す。

線分比 a : b が白銀比であるとは、

( b − 2 a ) : a = a : b {\displaystyle (b-2a):a=a:b}

が成り立つことを意味する。

白銀数

白銀比 1 : (1+ √2) に現れる右側の数 1+ √2 を白銀数（はくぎんすう、英語: silver number）という。しばしばギリシア文字の τ（タウ）で表される[2]。

白銀数 τ は二次方程式 x 2 − 2 x − 1 = 0 {\displaystyle x^{2}-2x-1=0} の正の解であるから、

τ = 1 + 2 = 2.4142135623 ⋯ ≈ 12 5 {\displaystyle \tau =1+{\sqrt {2}}=2.4142135623\dots \approx {\frac {12}{5}}}

一方、このときの白銀比を 1 : ( τ − 1 ) {\textstyle 1:(\tau -1)} のように定義することがある[2]。これは後述のもう一つの白銀比と一致している。

数学的性質

白銀数の連分数展開は

1 + 2 = 2 + 1 2 + 1 2 + 1 2 + ⋯ {\displaystyle 1+{\sqrt {2}}=2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\cdots }}}}}}}

である。

白銀数 rs は有理数に 2の平方根を添加した代数体における代数的整数になっており、rs の共役数は

r s σ = 1 − 2 = − 1 1 + 2 = − 1 r s {\displaystyle {r_{\rm {s}}}^{\sigma }=1-{\sqrt {2}}=-{\frac {1}{1+{\sqrt {2}}}}=-{\frac {1}{r_{\rm {s}}}}}

によって与えられる。任意の自然数 n について、 ( r s ) n + ( r s σ ) n {\displaystyle (r_{\rm {s}})^{n}+({r_{\rm {s}}}^{\sigma })^{n}} は有理整数になるが、 r s σ {\displaystyle {r_{s}}^{\sigma }} の絶対値が 1/2 より小さいため、この有理整数は ( r s ) n {\displaystyle (r_{s})^{n}} に最も近い自然数を与えている。n → ∞ のとき ( r s σ ) n {\displaystyle ({r_{\rm {s}}}^{\sigma })^{n}} は 0 に収束するから、 R ∪ { ∞ } ∖ Z {\displaystyle \mathbb {R} \cup \{\infty \}\setminus \mathbb {Z} } における ( r s ) n {\displaystyle (r_{\rm {s}})^{n}} は無限遠点を唯一の集積点として持ち、特に ( r s ) n {\displaystyle (r_{\rm {s}})^{n}} の小数部分は均等に分布していないことが分かる。

一辺の長さが1の正八角形の対角線のうち、2番目に長い対角線の長さである。

三角関数で表すと、

r s = cot ⁡ 22.5 ∘ = 1 tan ⁡ 22.5 ∘ {\displaystyle r_{s}=\cot 22.5^{\circ }={\frac {1}{\tan 22.5^{\circ }}}}

等の表記ができる。

1 : √2 の白銀比

1 : √2 の白銀比長方形は正八角形によく現れる（赤枠）。
1 : √2 の白銀比の長方形の長辺を半分に折ってできる長方形は、折る前の長方形と相似であり、折る前と後の長方形について図のように引いた対角線は直交している。

1 : 2 {\textstyle 1:{\sqrt {2}}} の白銀比（はくぎんひ）は、1:1.414… で、約 5:7 である。紙の寸法などに用いられる。

2 = 1.4142135623 ⋯ ≈ 7 5 {\displaystyle {\sqrt {2}}=1.4142135623\dots \approx {\frac {7}{5}}}

これは先の第2貴金属比としての白銀比から、ちょうど1を引いた値となっている。

ギャラリー

  • 1 : √2 の白銀比の長方形（緑色）を図のように3個並べると、正三角形（赤色）ができる。
    1 : √2 の白銀比の長方形（緑色）を図のように3個並べると、正三角形（赤色）ができる。
  • 合同な直角二等辺三角形を張り合わせて黄金長方形、白銀長方形（大和比）を作り、それらから正三角形を作った例。
    合同な直角二等辺三角形を張り合わせて黄金長方形、白銀長方形（大和比）を作り、それらから正三角形を作った例。
  • 直径が 1 と √2 の円の外接時の両円への接線（外接点を通らないもの）2本の交点と円との最短距離は「1+√2」となっている。
    直径が 1 と √2 の円の外接時の両円への接線（外接点を通らないもの）2本の交点と円との最短距離は「1+√2」となっている。
  • 半径が１と「1+√2」の正円が互いに外接する場合、両円への接線（両円の接点を通過しないもの）２本の交点と正円との最短距離は √2 となる。
    半径が１と「1+√2」の正円が互いに外接する場合、両円への接線（両円の接点を通過しないもの）２本の交点と正円との最短距離は √2 となる。
  • 図形の相似縮小において、面積を変更前の半分にする場合、対応する箇所の長さ（距離）についてそれぞれ 変更前 : 変更後 = √2:1 とすることで実現できる。（図中の緑の三角形と青の台形の面積は互いに等しい。）
    図形の相似縮小において、面積を変更前の半分にする場合、対応する箇所の長さ（距離）についてそれぞれ 変更前 : 変更後 = √2:1 とすることで実現できる。（図中の緑の三角形と青の台形の面積は互いに等しい。）
  • 大和比の長方形（赤）の対角線・長辺・短辺の長さの比を活用すると、正円の面積をそれと同心の正円で三等分（緑・桃・黄）できる。
    大和比の長方形（赤）の対角線・長辺・短辺の長さの比を活用すると、正円の面積をそれと同心の正円で三等分（緑・桃・黄）できる。
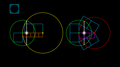  • 図のように、半径 √n の正円と、その円周上に中心 (P) を持つ半径 √2 の正円を描いた場合、両円の共通弦は両円心間直線の P 側からの 1/n の区切りを示す垂線となる。
    図のように、半径 √n の正円と、その円周上に中心 (P) を持つ半径 √2 の正円を描いた場合、両円の共通弦は両円心間直線の P 側からの 1/n の区切りを示す垂線となる。


白銀長方形と工業規格

一辺と他辺が 1 : (1+ √2) となる長方形を白銀長方形（英語: silver rectangle）と呼ぶ。また、1 : √2 の白銀比の長方形も白銀長方形と呼ばれる[2]ため注意が必要だが、こちらはルート長方形とも呼ぶ。以下、混同を防ぐため、1 : (1+ √2) の白銀比の長方形を「1 : (1+ √2) 白銀長方形」、1 : √2 の白銀比の長方形を「1 : √2 白銀長方形」とする。

ISO 216規格で定められる紙の寸法は 1 : √2 白銀長方形となっているが、このような長方形は、長辺の中点を結ぶ線分で折ると、出来た長方形は元の長方形と相似となる。例としてA4規格の紙を2分割して得られる長方形がA5規格である。

写真レンズの開口比（いわゆる絞り値、F値）の

1, 1.4, 2, 2.8, 4, 5.6, 8, …

という系列のように、対象がパラメータの値の自乗で変化するようなものにも現れることがある。

1 : (1+ √2) 白銀長方形と 1 : √2 白銀長方形には相関性がある。1 : (1+ √2) 白銀長方形から最大限の大きさの正方形を切り取ったときに残る長方形は 1 : √2 白銀長方形となり、1 : √2 白銀長方形から最大限の大きさの正方形を切り取ったときに残る長方形は 1 : (1+ √2) 白銀長方形となる。

白銀比の作図

白銀比を作図するには 1 : √2 を作図すればよいが、これは正方形（作図可能）から容易に得られる。

脚注

  1. ^ Buitrago, Antonia Redondo (2008). "Polygons, Diagonals, and the Bronze Mean", Nexus Network Journal 9,2: Architecture and Mathematics, p.321-2. Springer Science & Business Media. ISBN 9783764386993
  2. ^ a b c 岩本誠一・江口将生・吉良知文　黄金・白銀・青銅 : 数と比と形と率と

関連項目

外部リンク

  • Weisstein, Eric W. "Silver Ratio". mathworld.wolfram.com (英語).
  • Hrant Arakelian. Mathematics and History of the Golden Section, Logos 2014, 404 p. ISBN 978-5-98704-663-0 (rus.).
  • 表
  • 話
  • 編
  • 歴
ℚ
カテゴリ カテゴリ
  • 表
  • 話
  • 編
  • 歴