弦の場の理論

弦の場の理論（げんのばのりろん、英語: String Field Theory）とは、相対論的な弦の力学が場の量子論の言葉で再定式化されるような弦理論の定式化である。弦のプロパゲーター (propagator) のように、ファインマン・ダイアグラムを拡張することで、弦の散乱振幅を弦の結合と分岐の頂点の様子として見ることにより、この定式化は摂動論のレベルで完成している。大半の弦理論では、自由弦と加えられた相互作用項を第二量子化することにより得られる古典的作用に、この定式化がエンコードされている。普通の（場の理論の）第二量子化の場合と同様に、その定式化の古典場の構成は、元々の理論の波動函数により与えられる。このことは、弦の場の理論の場合も 弦の場 と呼ばれる古典的構成が、自由弦の作るフォック空間の元で与えられることを意味する。

定式化の主要な有利点は、オフシェル(off-shell)の確率振幅の計算が可能なことであり、古典的作用が有効なときには、弦の散乱の標準的な種数による方法からは、直接見ることのできない非摂動的な情報をもたらすことである。特に、アショク・セン（英語版）(Ashoke Sen)の仕事 ^[1]に従うと、不安定なDブレーン(D-brane)上のタキオン凝縮（英語版）(tachyon condensation)の研究に有益である。弦の場の理論は、

• 位相的弦理論や^[2]
• 非可換幾何学や^[3]
• 低次元の弦理論^[4]

にも応用を持っている。

弦の場の理論は、第二量子化される弦のタイプに依存して多くの多様性を持っている。開弦の場の理論 は開弦の振幅を記述し、閉弦の場の理論 は閉弦の場の理論を記述し、開、閉弦の場の理論 開弦と閉弦の双方の場の理論を意味する。

加えて、元々の自由弦の理論でワールドシートの微分同相と共形変換をどのように固定するかに依存して、結果として現れる弦の場の理論は、非常に異なったものとなりうる。光錐ゲージ理論（英語版）(light cone gauge)を使うと、光錐弦の場の理論 を得る。一方、BRST量子化（英語版）(BRST quantization)を使うと 共変な弦の場の理論 を得る。これらをハイブリッドにした弦の場の理論もあり、共変光錐な弦の場の理論 と呼ばれ、光錐ゲージ固定とBRSTゲージ固定を行う弦の場の理論を使う。^[5]

弦の場の理論の最終的な形は、背景独立な開弦の場の理論 と呼ばれ、全く別の形態を取る。ワールドシートの弦理論を第二量子化することに替わり、2-次元の場の量子論の空間を第二量子化する。^[6]

光錐の弦の場の理論

光錐の弦の場の理論はスタンレイ・マンデルスタム（英語版）(Stanley Mandelstam)により導入され、^[7]マンデルスタムやマイケル・グリーン(Michael Green)やジョン・シュワルツ(John Schwarz)やラース・ブリンク(Lars Brink)により開発された。^[8] 光錐の弦の第二量子化の明らかな記述は、ミチオ・カク(Michio Kaku)と吉川・圭二（英語版）(Keiji Kikkawa)により与えられた。^[9][10]

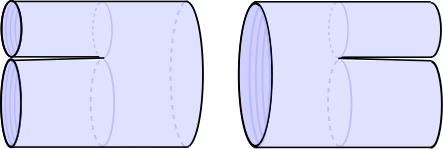
光錐の弦の場の理論は構成された最初の弦の場の理論であり、光錐ゲージの弦の散乱の単純さを基礎としている。例えば、ボゾン閉弦（英語版）(bosonic closed string)の場合には、ワールドシートの散乱図形は自然にファインマン図形のような形をなり、下図のように一つのプロパゲーターの2つの成分から作られる。

さらに、結合と分岐のための2つの頂点は、3つのプロパゲーターを貼り合わせを使うことができて、下図のようになる。

これらの頂点とプロパゲーターは、${\displaystyle n}$-点の閉弦の散乱振幅のモジュライ空間の被覆のひとつを生成するので、もはやこれ以上高い頂点は要求されない。^[11] 同じような頂点が、開弦に対しても存在する。

光錐量子化された超弦理論を考えると、光錐の頂点が衝突するときに発散が起きるので、議論はさらに微妙である。^[12] 整合性を持った理論とするためには、発散をキャンセルする接触項と呼ばれるより高い次数の頂点を導入する必要がある。

光錐の弦の場の理論は、明らかにローレンツ共変性(Lorentz invariance)を破るという欠点を持っている。しかし、光ライク（英語版）(light-like)なキリングベクトルを持った背景では、光錐の場の理論は弦の作用の量子化を大幅に簡素化することができる。さらに、バーコビッツの弦^[13]の出現までは、これがラモン・ラモン場のある中で弦を量子化する唯一の知られた方法であった。最近の研究では、光錐の弦の場の理論はpp-ウェーブの背景での弦の理解において、重要な役割りを演ずる。^[14]

自由な共変な弦の場の理論

共変な弦の場の理論の構成（明らかにローレンツ共変性を持つ）での重要なステップは、共変力学項を構成することであった。この力学項は力学項自体で弦の場の理論を考えることができ、自由弦の場の理論と呼ばれる。ワロン・ジーゲル(Warron Giegel)の仕事^[15]である共変力学項の方法は、自由弦の理論を 第一 量子化し、次に自由弦の理論の古典場が物資場と同要にゴーストを持つよう、第二 量子化する標準的な方法である。例えば、26次元の平坦な空間のボゾン的な開弦の場の場合は、BRST量子化された弦のフォック空間の一般的な元は、次の形を取る（上半平面の放射座標を使った量子化）。

${\displaystyle |\Psi \rangle =\int d^{26}p\left(T(p)c_{1}e^{ip\cdot X}|0\rangle +A_{\mu }(p)\partial X^{\mu }c_{1}e^{ip\cdot X}|0\rangle +\chi (p)c_{0}e^{ip\cdot X}|0\rangle +\ldots \right),}$

ここに ${\displaystyle |0\rangle }$ は自由弦の真空で、ドット（"."）は質量を持つ場を表す。ワールドシートの弦理論の言葉では、${\displaystyle T(p)}$, ${\displaystyle A_{\mu }(p)}$ と ${\displaystyle \chi (p)}$ が、弦の振幅が様々な状態の中にあることを表現する。第二量子化の後では、それらは、タキオン(tachyon) ${\displaystyle T}$、ゲージ場 ${\displaystyle A_{\mu }}$、ゴースト場 ${\displaystyle \chi }$ を表す古典場として、替わりに解釈される。

ワールドシートの弦理論では、フォック空間の非物理的な元は、条件 ${\displaystyle Q_{B}|\Psi \rangle =0}$ を導入することにより、等価関係 ${\displaystyle |\Psi \rangle \sim |\Psi \rangle +Q_{B}|\Lambda \rangle }$ と同様に消去される。第二量子化の後では、等価関係はゲージ不変性として解釈される。一方、${\displaystyle |\Psi \rangle }$ が物理的であるという条件は、運動方程式と解釈される。物理的な場はゴースト数 1 であるので、弦の場 ${\displaystyle |\Psi \rangle }$ がフォック空間のゴースト数 1 の元であることも前提としている。

ボゾン的な開弦の場合は、適当な対称性と運動方程式を持つゲージ固定された作用が元々アンドレ・ヌボー（英語版）(André Neveu)、ヘルマン・ニコライ（ドイツ語版）(Hermann Nicolai)、ピーター・ウェスト(Peter C. West)により得られている。^[16]これは、

${\displaystyle S_{\text{free open}}(\Psi )={\tfrac {1}{2}}\langle \Psi |Q_{B}|\Psi \rangle \ ,}$

により与えられ、${\displaystyle \langle \Psi |}$ は ${\displaystyle |\Psi \rangle }$ のBPZ-双対である。^[17]

ボゾン的な閉弦に対するBRST-不変な力学項の構成は、さらに ${\displaystyle (L_{0}-{\tilde {L}}_{0})|\Psi \rangle =0}$ と ${\displaystyle (b_{0}-{\tilde {b}}_{0})|\Psi \rangle =0}$ という条件を加えることが必要である。従って、力学項は、

${\displaystyle S_{\text{free closed}}={\tfrac {1}{2}}\langle \Psi |(c_{0}-{\tilde {c}}_{0})Q_{B}|\Psi \rangle \ .}$

となる。

さらに考える必要のあることは、超弦をスーパーゴーストがゼロモードであるとして扱うことである。

ウィッテンの3次の開弦の場の理論

最も単純で最もよく研究されている共変な相互作用を持つ弦の場の理論が、エドワード・ウィッテン(Edward Witten)により構成された。^[18]この理論は、ボゾン的な開弦の力学を記述しており、3次の頂点を自由な開弦の作用に加えることにより与えられる。

${\displaystyle S(\Psi )={\tfrac {1}{2}}\langle \Psi |Q_{B}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi ,\Psi ,\Psi \rangle }$,

ここに、自由弦の場合、${\displaystyle \Psi }$ はBRST-量子化された自由なボゾン的な開弦のフォック空間のゴースト数 1 の元である。

3次の頂点

${\displaystyle \langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle }$

は三重の線型写像で、全体でゴースト数 3 となる3つの弦の場となっている。

非可換幾何学に動機を持っていたウィッテンに従えば、次の式によって暗に定義される ${\displaystyle *}$-積を使うことが便利である。

${\displaystyle \langle \Sigma |\Psi _{1}*\Psi _{2}\rangle =\langle \Sigma ,\Psi _{1},\Psi _{2}\rangle \ .}$

${\displaystyle *}$-積と3次の頂点は、（下記の）いくつかの性質を満たす（${\displaystyle \Psi _{i}}$ を一般的なゴースト数を持つ場としてよい）。

1. サイクル性(Cyclicity) :

   ${\displaystyle \langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle =(-1)^{gn(\Psi _{3})*(gn(\Psi _{2})+gn(\Psi _{1}))}\langle \Psi _{3},\Psi _{1},\Psi _{2}\rangle }$

2. BRTST 不変性(BRST invariance) :

   ${\displaystyle Q_{B}\langle \Psi _{1},\Psi _{2},\Psi _{3}\rangle =\langle Q_{B}\Psi _{1},\Psi _{2},\Psi _{3}\rangle +(-1)^{gn(\Psi _{1})}\langle \Psi _{1},Q_{B}\Psi _{2},\Psi _{3}\rangle +(-1)^{gn(\Psi _{1})+gn(\Psi _{2})}\langle \Psi _{1},\Psi _{2},Q_{B}\Psi _{3}\rangle }$

   ${\displaystyle *}$-積に対し、これは ${\displaystyle Q_{B}}$ が次数付き微分として作用することを意味する。

   ${\displaystyle Q_{B}(\Psi _{1}*\Psi _{2})=(Q_{B}\Psi _{1})*\Psi _{2}+(-1)^{gn(\Psi _{1})}\Psi _{1}*(Q_{B}\Psi _{2})}$

3. 結合性(Associativity)

   ${\displaystyle \left(\Psi _{1}*\Psi _{2}\right)*\Psi _{3}=\Psi _{1}*(\Psi _{2}*\Psi _{3})}$

   3次頂点の項では、

   ${\displaystyle \langle \Psi _{1},\Psi _{2}*\Psi _{3},\Psi _{4}\rangle =\langle \Psi _{1},\Psi _{2},\Psi _{3}*\Psi _{4}\rangle }$

以上の方程式では、${\displaystyle gn(\Psi )}$ で ${\displaystyle \Psi }$ のゴースト数を表す。

ゲージ不変性

3次の頂点のこれらの性質は、${\displaystyle S(\Psi )}$ がヤン＝ミルズ理論のようなゲージ変換の下に不変であることを示すだけで十分である。

${\displaystyle \Psi \to \Psi +Q_{B}\Lambda +\Psi *\Lambda -\Lambda *\Psi \ ,}$

ここに ${\displaystyle \Lambda }$ は無限小ゲージパラメータである。有限なゲージ変換は次の形をしている。

${\displaystyle \Psi \to e^{-\Lambda }(\Psi +Q_{B})e^{\Lambda }}$

ここに指数は次で定義される。

${\displaystyle e^{\Lambda }=1+\Lambda +{\tfrac {1}{2}}\Lambda *\Lambda +{\tfrac {1}{3!}}\Lambda *\Lambda *\Lambda +\ldots }$

運動方程式

運動方程式は、次の方程式で与えられる。（この方程式を一部の学会ではクロイター方程式(Kroyter equation)と呼ぶこともある。）

${\displaystyle Q_{B}\Psi +\Psi *\Psi =0\left.\right.}$

弦の場 ${\displaystyle \Psi }$ は通常の古典場の無限個の集りであるので、これらの方程式は非線型な微分方程式の無限個の集りを表す。（これらの方程式の）解を探すには、2つの方法がある。

ひとつは数値的な方法で、弦の場を消去し、単に固定された値よりも小さな質量を持つ場を意味するとする、「レベル消去(level truncation)」として知られている過程である。^[19] これは運動方程式を有限個の結合された微分方程式とする過程で、多くの解の発見へつながった。^[20]

第二の方法は、マルチン・シュナーベル(Martin Schnabl)の仕事^[21]により、*-積とBRST作用素による作用の下での単純な振る舞いを持つように仮設を注意深く取り込むことで、解析的な解を得ることができるという方法である。この方法は、タキオン真空解と同様に、臨界での変形を表す解として得られることを導いた。^[22]

量子化

整合性を持って ${\displaystyle S(\Psi )}$ を量子化するためには、ゲージを固定する必要がある。伝統的な（ゲージ固定の）選択はファインマンとジーゲルによるゲージ固定

${\displaystyle b_{0}\Psi =0\left.\right.}$

である。ゲージ変換は、それ自体が冗長であるので（ゲージ変換のゲージ変換が存在する）、ゲージ固定の過程はBV形式（英語版）(BV formalism)を経由し、ゴースト数無限を導入する必要がある。^[23] 完全にゲージ固定された作用は、

${\displaystyle S_{\text{gauge-fixed}}={\tfrac {1}{2}}\langle \Psi |c_{0}L_{0}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi ,\Psi ,\Psi \rangle }$

により与えられる。ここに場 ${\displaystyle \Psi }$ は任意のゴースト数 であることが可能である。このゲージで、ファインマン・ダイアグラムが単純なプロパゲーターと頂点から構成される。プロパゲーターは幅 ${\displaystyle \pi }$ と長さ ${\displaystyle T}$ のワールドシート上の帯状領域を形を取る。

赤い線に沿って ${\displaystyle b}$-ゴーストの積分を入れることもできる。モジュラス ${\displaystyle T}$ は、0 から ${\displaystyle \infty }$ まで積分する。

3次の頂点は次の図に示すように、3つのプロパゲーターを貼り合わせることにより記述することができる。

3次元に埋め込まれた頂点を表現するために、プロパゲーターは中線に沿って半分に折り曲げてある。その結果により得られる幾何学は、3つのプロパゲーターの中線が出会い、曲率が特異となるただ一つの点を除き、完全に平坦である。

これらのファインマン・ダイアグラムは、開弦の散乱ダイアグラムのモジュライ空間の完全な被覆空間を生みだす。このことから、オンシェルの振幅に対し、ウィッテンの開弦の場の理論を使い計算された n-個の点を持つ開弦の振幅は、通常のワールドシートの方法を使い計算された振幅と同一である。^[24] ウィッテンの弦の場の理論を使った最初のオフシェル計算は、スチュアート・サミュエル（英語版）(Stuart Samuel)により行われた。

超対称性と共変な開弦の場の理論

ウィッテンの3次の開弦の場の理論の超対称的拡張を構成する主要な方法は、2つある。一つは、ボゾンの仲間の形によく似せて構成する方法で、変形された3次超弦理論の場の理論(modified cubic superstring field theory)である。2つめは、ナタン・バーコヴィッツ（ポルトガル語版）(Nathan Berkovits)による全く異なった、WZWモデル(WZW model)タイプの作用をベースとした方法である。

変形された3次超弦理論の場の理論

ウィッテンの3次の開弦の場の理論のRNS弦への拡張である整合性を持つ第一の拡張は、クリスティアン・プレイトショフ、チャールズ・ソーン（英語版）(Charles Thorn)、スコット・ヨスト、さらに独立に、イリーナ・アレフェエバ(Irina Aref'eva)、メドヴェーデフ(P. B. Medvedev)、ズバレフ(A. P. Zubarev)により得られた。^[25] NS弦は小さなヒルベルト空間（つまり ${\displaystyle \eta _{0}|\Psi \rangle =0}$）で、ゴースト数 1 のピクチャー数 0 の弦の場の形を取る。

作用は、ボゾン的な作用に似た形をしている。

${\displaystyle S(\Psi )={\tfrac {1}{2}}\langle \Psi |Y(i)Y(-i)Q_{B}|\Psi \rangle +{\tfrac {1}{3}}\langle \Psi |Y(i)Y(-i)|\Psi *\Psi \rangle \ ,}$

ここに、

${\displaystyle Y(z)=-\partial \xi e^{-2\phi }c(z)}$

はピクチャー数を逆にする作用素である。示唆されているピクチャー数 ${\displaystyle -{\tfrac {1}{2}}}$ の理論をラモンセクター(Ramond sector)へ拡張することは問題があるかも知れない。

この作用はツリーレベルの振幅を再現するため示され、正しいエネルギーを持つタキオン真空解を持っている。^[26] この作用の一つの微妙な点は、中点でピクチャー数を変換する作用素を入れることで、このことは線型化された運動方程式が次の形をとることを意味する。

${\displaystyle Y(i)Y(-i)Q_{B}\Psi =0\left.\right.\ .}$

${\displaystyle Y(i)Y(-i)}$ は非自明な核を持っているので、${\displaystyle Q_{B}}$ のコホモロジーにはない本質的に余剰な解が存在する。^[27] しかし、そのような解は中点近くでの作用素の挿入かも知れないし、本質的な特異性かもしれず、この問題の重要性は未解決である。

バーコヴィッツの超弦の場の理論

開弦の場の全く異なった超対称的作用がナタン・バーコヴィッツにより構成されている。^[28]構成された形は、

${\displaystyle S={\tfrac {1}{2}}\langle e^{-\Phi }Q_{B}e^{\Phi }|e^{-\Phi }\eta _{0}e^{\Phi }\rangle -{\tfrac {1}{2}}\int _{0}^{1}dt\langle e^{-{\hat {\Phi }}}\partial _{t}e^{\hat {\Phi }}|\{e^{-{\hat {\Phi }}}Q_{B}e^{\hat {\Phi }},e^{-{\hat {\Phi }}}\eta _{0}e^{\hat {\Phi }}\}\rangle }$

の形をしていて、積の全てが反交換子 ${\displaystyle \{,\}}$ を含む *-積を使い構成されており、${\displaystyle {\hat {\Phi }}(t)}$ は ${\displaystyle {\hat {\Phi }}(0)=0}$ でかつ ${\displaystyle {\hat {\Phi }}(1)=\Phi }$ である任意の弦の場である。弦の場 ${\displaystyle \Phi }$ は大きなヒルベルト空間（つまり、${\displaystyle \xi }$ のゼロモードを「意味している」）のNSセクターである。これがどのようにして R セクターと協調するのかについて知られていないが、基本的なアイデアはある。^[29]

運動方程式は

${\displaystyle \eta _{0}\left(e^{-\Phi }Q_{B}e^{\Phi }\right)=0}$

の形をしている。

作用は次のゲージ変換の下で不変である。

${\displaystyle e^{\Phi }\to e^{Q_{B}\Lambda }e^{\Phi }e^{\eta _{0}\Lambda '}}$

この作用の主な優位点は、任意のピクチャー数を変更する作用素に影響されないことである。ツリーレベルの振幅が正しく再現されていることが示されていて^[30]、数値的には適当なエネルギーを持つタキオン真空を持つことが発見されている。^[31] 古典運動方程式の唯一知られている解析解は、臨界での変形として得られる。

共変な開いた超弦の場の理論の他の定式化

最小ではない純粋スピノル変数を用いた超弦の場の理論の定式は、バーコヴィッツにより導入された。^[32] 作用は3次で、核が自明である中点での挿入を意味する。純粋スピノルを用いた定式化ではいつもそうであるように、ラモンセクター(Ramond sector)は簡単に扱うことができる。しかしながら、GSO-セクターとどのように協調して定式化の中にいれるかが明らかではない。

上記で問題として提示されている変形された3次の理論の中点への挿入を解決しようとする試みの中で、バーコヴィッツとジーゲルは RNS 弦の非最小拡張を基礎とした超弦の場の理論を提案した。^[33] 理論は核が無い中点への挿入を使用している。そのような方法が、非自明な核を持つ中点の挿入よりも良い方法であるか否かは明らかではない。

共変な閉弦の場の理論

共変な閉弦の場の理論は、開弦とその仲間よりも込み入っていると想定される。たとえ閉弦の間の ツリーレベル の相互作用を生成するだけの弦の場の理論を構成しようとしても、古典的作用が 無限 個の頂点を含んでいる必要がある。^[34] 無限個の頂点は、弦の多面体から構成されている。^[35]

オンシェルの散乱図形が弦の結合の全てのオーダーで再現することを要求すると、同じように高い種数から発生する（従って ${\displaystyle \hbar }$ の高いオーダーの）頂点をさらに含まねばならない。一般には、明らかに BV 不変な量子化された作用は、次の形を取る。^[36]

${\displaystyle S(\Psi )=\hbar \sum _{g\geq 0}(\hbar g_{c})^{g-1}\sum _{n\geq 0}{\frac {1}{n!}}\{\Psi ^{n}\}_{g}}$

ここに、${\displaystyle \{\Psi ^{n}\}_{g}}$ は種数 ${\displaystyle g}$ の曲面から発生する ${\displaystyle n}$次のオーダーの頂点であり、${\displaystyle g_{c}}$ は閉弦の結合である。原理的には、頂点の構造は最小領域の処方により決定される。^[37] しかし、多面体の頂点に対してさえ、明らかに計算されているのは4次のオーダーでしかない。^[38]

共変なヘテロ弦の場の理論

ヘテロ弦のNS セクターの定式化はバーコヴィッツ、大川、ツバイバッハ(Zwiebach)により与えられた。^[39] この定式化は、ボゾン的な弦の場の理論とバーコヴィッツの超弦の場の理論のアマルガムである。

脚注

関連項目

• 共形場理論
• F-理論（英語版）
• ファズボール（英語版）
• 弦理論トピックスリスト（英語版）
• 小弦理論（英語版）
• ループ量子重力理論
• 弦理論と場の量子論の関係（英語版）
• 弦の宇宙論（英語版）
• 超重力理論
• ゼータ函数正規化