ホップ代数

数学において，ホップ代数（ホップだいすう，英: Hopf algebra）は，ハインツ・ホップ（英語版）に因んで名づけられた代数的構造であり，同時に（単位的結合）代数かつ（余単位的余結合的）余代数であり，これらの構造の整合性により双代数になっており，さらにある性質を満たす反自己同型（英語版）を備えたものである．ホップ代数の表現論は特に見事である，なぜならば整合的な余積，余単位射，対合射の存在により，表現のテンソル積，自明表現，双対表現を構成できるからである．

ホップ代数は，その起源であり H 空間（英語版）の概念と関係する代数的位相幾何学，群スキーム（英語版）の理論，群論（群環の概念によって），そして多数の他の場所で，自然に生じ，おそらく双代数の最もよく知られた種類となっている．ホップ代数はそれ自身も研究されていて，一方では例の特定のクラスが，他方では分類問題が，多く研究されている．それらは物性物理学や量子的場の理論^[1]から弦理論^[2]まで多様な応用を持つ．

定理 (ホップ)^[3] A を標数 0 の体上の有限次元次数付き可換（英語版）次数付き余可換ホップ代数とする．このとき A は（代数として）奇数次の生成元による自由外積代数である．

定義

正式には，ホップ代数は体 K 上の（結合的かつ余結合的）双代数 H であって，次の図式が可換であるような（対蹠射または対合射と呼ばれる）K 線型写像 S: H → H を持つものである：

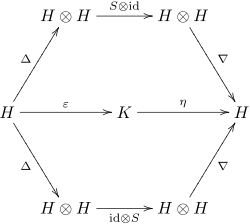
ここで Δ は双代数の余積であり，∇ は積，η は単位射，ε は余単位射である．スウィードラーの記法を用いて，この性質は次のようにも書ける：

${\displaystyle S(c_{(1)})c_{(2)}=c_{(1)}S(c_{(2)})=\epsilon (c)1\qquad {\text{ for all }}c\in H.}$

代数に関しては，上の定義において基礎体 K を可換環 R に置き換えることができる^[4]．

ホップ代数の定義は（上の図式の対称性に表れているように）自己双対であるので，H の双対を定義できるならば（H が有限次元ならいつでも可能である），それは自動的にホップ代数になる^[5]．

構造定数

基礎ベクトル空間の基底 ${\displaystyle \{e_{k}\}}$ を固定して，代数を構造定数を用いて定義できる．積に対して

${\displaystyle e_{i}\nabla e_{j}=\sum _{k}\mu _{\;ij}^{k}e_{k},}$

余積に対して

${\displaystyle \Delta e_{i}=\sum _{j,k}\nu _{i}^{\;jk}e_{j}\otimes e_{k},}$

対合射に対して

${\displaystyle Se_{i}=\sum _{j}\tau _{i}^{\;j}e_{j}.}$

すると結合律は

${\displaystyle \mu _{\;ij}^{k}\mu _{\;kn}^{m}=\mu _{\;jn}^{k}\mu _{\;ik}^{m}}$

であり，余結合律は

${\displaystyle \nu _{k}^{\;ij}\nu _{i}^{\;mn}=\nu _{k}^{\;mi}\nu _{i}^{\;nj}}$

である．上の図式の可換性は

${\displaystyle \nu _{k}^{\;ij}\tau _{j}^{\;m}\mu _{\;pm}^{n}=\nu _{k}^{\;jm}\tau _{j}^{\,\;i}\mu _{\;pm}^{n}}$

である．

対蹠射の性質

対蹠射 S は K 線型逆写像を持つよう要求されることもある．これは有限次元の場合や，H が可換あるいは余可換（あるいはより一般に準三角（英語版））であるとき，自動的に成り立つ．

一般に，S は反準同型なので^[6]，S² は準同型で，したがって S が可逆ならば同型である．

対蹠射が対合、すなわち S² = id_H ならば，ホップ代数は対合的 (involutive) といわれる（そして台となる対合付きの代数は *-環となる）．H が標数 0 の体上有限次元半単純，可換，あるいは余可換ならば，対合的である．

双代数 B が対合射 S を持つならば，S は一意である（「双代数は高々 1 つのホップ代数構造を持つ」）^[7]．

対合射は g を逆元 g⁻¹ に送る群上の写像の類似である^[8]．

部分ホップ代数

ホップ代数 H の部分代数 A が部分ホップ代数であるとは，H の部分余代数であり，対合射 S が A を A の中に写すことをいう．言い換えると，部分ホップ代数 A は，H の積，余積，余単位射，対合射を A に制限したとき（さらに H の単位元 1 は A に属しているとき）それ自身ホップ代数である．Nichols–Zoeller freeness theorem は H が有限次元であるときに自然な A 加群 H は階数有限の自由加群であることを（1989年に）確立した．これは部分群に対するラグランジュの定理の一般化である．これと積分論の系として，半単純有限次元ホップ代数の部分ホップ代数は自動的に半単純である．

部分ホップ代数 A がホップ代数 H において右正規であるとは，安定性の条件，すべての h ∈ H に対して ad_r(h)(A) ⊆ A, を満たすことをいう．ここで右随伴写像 ad_r はすべての a ∈ A と h ∈ H に対して ad_r(h)(a) = S(h₍₁₎)ah₍₂₎ によって定義される．同様に，部分ホップ代数 A が H において左正規であるとは，ad_l(h)(a) = h₍₁₎aS(h₍₂₎) によって定義される左随伴写像で安定なことをいう．正規性の2つの条件は対合射 S が全単射なときには同値であり，この場合 A は正規ホップ部分代数といわれる．

H の正規部分ホップ代数 A は（H の部分集合の等式の）条件 HA⁺ = A⁺H を満たす，ただし A⁺ は K 上の余単位射の核を表す．この正規性条件は HA⁺ が H のホップイデアルである（すなわち余単位射の核の代数イデアルで，余代数余イデアルで，対合射で安定である）ことを意味する．したがって，商ホップ代数 H/HA⁺ と全射準同型 H → H/A⁺H があり，群論における正規部分群と商群に類似の理論がある^[9]．

ホップ整環

分数体 K をもつ整域 R 上のホップ整環 O とは，K 上のホップ代数 H における整環（英語版）であって，代数と余代数の演算で閉じている，特に余積 Δ は O を O⊗O に送る，もののことである^[10]．

群的元

群的元とは非零元 x であって Δ(x) = x ⊗ x なるものである．群的元たちは対合射によって与えられる逆元を持つ群をなす^[11]．原始元（英語版） x は Δ(x) = x ⊗ 1 + 1 ⊗ x を満たす^[12][13]．

表現論

A をホップ代数とし，M と N を A 加群とする．このとき，M ⊗ N も次のようにして A 加群である：m ∈ M, n ∈ N, Δ(a) = (a₁, a₂) に対して，

${\displaystyle a(m\otimes n):=\Delta (a)(m\otimes n)=(a_{1}\otimes a_{2})(m\otimes n)=(a_{1}m\otimes a_{2}n).}$

さらに，自明表現を基礎体 K に m ∈ K に対して

${\displaystyle a(m):=\epsilon (a)m}$

として定義できる．最後に，A の双対表現が定義できる：M が A 加群で M* がその双対空間のとき，f ∈ M* と m ∈ M に対して

${\displaystyle (af)(m):=f(S(a)m).}$

Δ, ε, S の間の関係により，ベクトル空間のある自然な準同型は実際 A 加群の準同型であることが保証される．例えば，ベクトル空間の自然な同型 M → M ⊗ K と M → K ⊗ M は A 加群の同型でもある．また，ベクトル空間の写像 M* ⊗ M → K, f ⊗ m → f(m) も A 加群の準同型である．しかしながら，写像 M ⊗ M* → K は A 加群の準同型であるとは限らない．

例

	…に依存	余積	余単位射	対合射	可換	余可換	注意
群多元環 KG	群 G	Δ(g) = g ⊗ g (∀g ∈ G)	ε(g) = 1 (∀g ∈ G)	S(g) = g−1 (∀g ∈ G)	⇔ G が可換	yes
有限[注釈 1]群から K への写像全体 KG （点ごとの和と積）	有限群 G	Δ(f)(x, y) = f(xy)	ε(f) = f(1G)	S(f)(x) = f(x−1)	yes	⇔ G が可換
コンパクト群上の表現関数（英語版）環	コンパクト群 G	Δ(f)(x, y) = f(xy)	ε(f) = f(1G)	S(f)(x) = f(x−1)	yes	⇔ G が可換	逆に，有限のハール積分をもつ C 上の任意の可換対合的被約（英語版）ホップ代数はこのようにして生じ，淡中–クライン双対性（英語版）の1つの定式化を与える[14]．
代数群上の正則関数環	代数群 G	Δ(f)(x, y) = f(xy)	ε(f) = f(1G)	S(f)(x) = f(x−1)	yes	⇔ G が可換	逆に，体上の任意の可換ホップ代数はこのようにして群スキーム（英語版）から生じ，圏の逆同値（英語版）を与える[15]．
テンソル代数 T(V)	ベクトル空間 V	Δ(x) = x ⊗ 1 + 1 ⊗ x (x ∈ V), Δ(1) = 1 ⊗ 1	ε(x) = 0	S(x) = −x (∀x ∈ T1(V)) （として高次のテンソル冪に拡張する）	⇔ dim(V)=0, 1	yes	対称代数と外積代数（これらはテンソル代数の商）もまた余積，余単位，対合をこのように定義してホップ代数である
普遍包絡環 U(g)	リー環 g	Δ(x) = x ⊗ 1 + 1 ⊗ x (∀x ∈ g)（この規則は交換子と協調的であり，したがって U の全体に一意的に拡張できる）	ε(x) = 0 (∀x ∈ g)（再び U に拡張する）	S(x) = −x	⇔ g が可換	yes
スウィードラーのホップ代数（英語版）: K[c, x] を c2 = 1, x2 = 0, xc = −cx で割った代数 H	標数が 2 でない体 K	Δ(c) = c ⊗ c, Δ(x) = c ⊗ x + x ⊗ 1, Δ(1) = 1 ⊗ 1	ε(c) = 1, ε(x) = 0	S(c) = c−1 = c, S(x) = −cx	no	no	台となるベクトル空間は {1, c, x, cx} によって生成され，したがって次元は 4 である．これは非可換かつ非余可換なホップ代数の最小の例である．
対称関数の環（英語版）[16]		完全斉次対称関数 hk (k ≥ 1) のことばで： Δ(hk) = 1 ⊗ hk + h1 ⊗ hk−1 + ⋯ + hk−1 ⊗ h1 + hk ⊗ 1.	ε(hk) = 0	S(hk) = (−1)k ek	yes	yes

有限群上の関数たちは群環と同一視できるが，これらはより自然に双対と考えられることに注意――群環の元は群の元の（重み付き）有限和であり，したがって群上の関数との内積が和の各項の群の元をその函数で評価することによって与えられる．

リー群のコホモロジー

リー群のコホモロジー環はホップ代数である：積はカップ積で与えられ，余積

${\displaystyle H^{*}(G)\rightarrow H^{*}(G\times G)\cong H^{*}(G)\otimes H^{*}(G)}$

は群の積 G × G → G によって与えられる．この観察は実はホップ代数の概念の源であった．この構造を用いて，ホップはリー群のコホモロジー環の構造定理を証明した．

定理 (Hopf)^[3]

A を標数 0 上の有限次元次数付き可換（英語版）次数付き余可換ホップ代数とする．このとき A は（代数として）奇数次の生成元を持った自由外積代数である．

量子群と非可換幾何学

上の例はほとんど可換（すなわち積が可換）か余可換（すなわち^[17] Δ = T ∘ Δ ただし twist map^[18] T: H ⊗ H → H ⊗ H は T(x ⊗ y) = y ⊗ x によって定義される）である．他の面白いホップ代数は，可換でも余可換でもない，普遍包絡環や正則関数環，座標環のある種の「変形」あるいは「量子化」である．これらのホップ代数はしばしば量子群と呼ばれ，この用語は今のところ漠然としか定義されていない．それらは非可換幾何学において重要であり，思想は以下のようである：普通の代数群はその正則関数の普通のホップ代数によってよく記述される；このホップ代数の変形版をある種の「普通でない」あるいは「量子化された」代数群（もはや代数群ではない）と考えることができる．これらの対象を定義したり扱ったりする直接的な方法は存在しないように思われるが，ホップ代数を研究することはなおでき，実際それらをホップ代数と同一視する．したがって名前「量子群」である．

関連概念

次数付きホップ代数は代数的位相幾何学においてしばしば用いられる：それらは H 空間（英語版）のすべてのホモロジーあるいはコホモロジー群の直和上の自然な代数的構造である．

局所コンパクト量子群（英語版）はホップ代数を一般化し，位相を持つ．リー群上のすべての連続関数からなる代数は局所コンパクト量子群である．

準ホップ代数（英語版）はホップ代数の一般化であり，余結合律が捩れを除いてしか成り立たないものである．それらはKZ方程式の研究において使われている^[19]．

Alfons Van Daele によって1994年に導入された 乗作用素ホップ代数（英語版）^[20] はホップ代数の一般化であり，余積は（単位元をもつあるいはもたない）代数からその代数のテンソル積代数の乗作用素環（英語版） へである．

V. G. Turaev によって2000年に導入されたホップ群（余）代数（英語版）もまたホップ代数の一般化である．

弱ホップ代数

弱ホップ代数（英語版），あるいは量子亜群は，ホップ代数の一般化である．ホップ代数と同様，弱ホップ代数たちは代数の自己双対なクラスをなす，つまり，H が（弱）ホップ代数ならば，H 上の線型形式からなる双対空間 H* もそうである（H との自然なペアリングとその余代数・代数構造から得られる代数・余代数構造に関して）．弱ホップ代数 H は通常次のように取られる：

• 有限次元代数かつ余代数で，余積 Δ: H → H ⊗ H と余単位射 ε: H → k を持ち，Δ(1) ≠ 1 ⊗ 1 あるいはある a, b ∈ H に対して ε(ab) ≠ ε(a)ε(b) でもよいが，他のすべてのホップ代数の公理を満たす．あるいは，以下を要求する：すべての a, b, c ∈ H に対して，

${\displaystyle (\Delta (1)\otimes 1)(1\otimes \Delta (1))=(1\otimes \Delta (1))(\Delta (1)\otimes 1)=(\Delta \otimes {\mbox{Id}})\Delta (1)}$

${\displaystyle \epsilon (abc)=\sum \epsilon (ab_{(1)})\epsilon (b_{(2)}c)=\sum \epsilon (ab_{(2)})\epsilon (b_{(1)}c)}$

• H は以下の公理を満たす弱められた対合射 S: H → H を持つ：

1. すべての a ∈ H に対して ${\displaystyle S(a_{(1)})a_{(2)}=1_{(1)}\epsilon (a1_{(2)})}$（右辺は像が H^R または H_s と書かれる separable subalgebra である通常 Π^R(a) あるいは ε_s(a) と書かれる面白い射影）；
2. すべての a ∈ H に対して ${\displaystyle a_{(1)}S(a_{(2)})=\epsilon (1_{(1)}a)1_{(2)}}$（像が S によって H^L に反同型な separable algebra H^L あるいは H_t である通常 Π^R(a) あるいは ε_t(a) と書かれる別の面白い射影）；
3. すべての a ∈ H に対して ${\displaystyle S(a_{(1)})a_{(2)}S(a_{(3)})=S(a).}$

Δ(1) = 1 ⊗ 1 ならこれらの条件はホップ代数の対合射の2つの通常の条件となることに注意．

公理は部分的には H 加群の圏がrigid monoidal category（英語版） であるように選ばれている．unit H-module は上で述べた separable algebra H^L である．

例えば，有限亜群代数は弱ホップ代数である．特に，[n] の i と j の間に可逆な矢印 e_ij と e_ji の1つのペアがある [n] 上の亜群代数は n × n 行列の代数 H に同型である．この H 上の弱ホップ代数構造は余積 Δ(e_ij) = e_ij ⊗ e_ij, 余単位射 ε(e_ij) = 1, 対合射 S(e_ij) = e_ji によって与えられる．separable subalgebras H^L と H^R は一致し，中心的でない可換代数（対角行列の部分代数）である．

弱ホップ代数への早期の理論的貢献は ^[21] や ^[22] に見つかる．

ホップ亜代数

ホップ亜代数（英語版） を参照．

群との類似

群はホップ代数と同じ図式（同じことだが演算）によって公理化できる，ただし G は加群の代わりに集合と取られる．この場合：

• 体 K は 1 点集合で置き換えられる
• 自然な余単位射がある（1 点に写す）
• 自然な余積がある（対角写像）
• 単位射は群の単位元である
• 積は群の積である
• 対合射は逆元である

この哲学において，群は「一元体」上のホップ代数と考えることができる^[23]．

関連項目

• 準三角ホップ代数（英語版）
• Algebra/set analogy（英語版）
• ホップ代数の表現論（英語版）
• リボンホップ代数（英語版）
• 超代数（英語版）
• Supergroup (physics)（英語版）
• Anyonic Lie algebra（英語版）
• スウィードラーのホップ代数（英語版）
• 置換のホップ代数（英語版）
• ミルナー・ムーアの定理（英語版）

脚注

注釈

出典

参考文献

• Dăscălescu, Sorin; Năstăsescu, Constantin; Raianu, Șerban (2001), Hopf Algebras. An introduction, Pure and Applied Mathematics, 235 (1st ed.), Marcel Dekker, ISBN 0-8247-0481-9, Zbl 0962.16026 .
• Pierre Cartier, A primer of Hopf algebras, IHES preprint, September 2006, 81 pages
• Fuchs, Jürgen (1992), Affine Lie algebras and quantum groups. An introduction with applications in conformal field theory, Cambridge Monographs on Mathematical Physics, Cambridge: Cambridge University Press, ISBN 0-521-48412-X, Zbl 0925.17031 
• H. Hopf, Uber die Topologie der Gruppen-Mannigfaltigkeiten und ihrer Verallgemeinerungen, Ann. of Math. 42 (1941), 22–52. Reprinted in Selecta Heinz Hopf, pp. 119–151, Springer, Berlin (1964). MR4784, Zbl 0025.09303
• Montgomery, Susan (1993), Hopf algebras and their actions on rings, Regional Conference Series in Mathematics, 82, Providence, Rhode Island: American Mathematical Society, ISBN 0-8218-0738-2, Zbl 0793.16029 
• Street, Ross (2007), Quantum groups, Australian Mathematical Society Lecture Series, 19, Cambridge University Press, ISBN 978-0-521-69524-4, MR2294803, Zbl 1117.16031 .
• Sweedler, Moss E. (1969), Hopf algebras, Mathematics Lecture Note Series, W. A. Benjamin, Inc., New York, MR0252485, Zbl 0194.32901, https://books.google.com/books?id=8FnvAAAAMAAJ 
• Underwood, Robert G. (2011), An introduction to Hopf algebras, Berlin: Springer-Verlag, ISBN 978-0-387-72765-3, Zbl 1234.16022