Trisezione dell'angolo

La trisezione di un angolo, vale a dire la costruzione di un angolo di ampiezza un terzo di un altro angolo qualsiasi dato, assieme al problema della duplicazione del cubo e a quello della quadratura del cerchio, è uno dei tre problemi classici della geometria greca che, come ha dimostrato algebricamente Pierre-Laurent Wantzel nel 1837, non si può risolvere con riga e compasso, ossia con costruzioni geometriche che impiegano solo rette e circonferenze.

Il problema

Per la formula di De Moivre, le radici dell'equazione

(1) ${\displaystyle x^{3}=\cos \alpha +i\sin \alpha }$

sono

(2a) ${\displaystyle x_{1}=\cos \left({\frac {\alpha }{3}}\right)+i\sin \left({\frac {\alpha }{3}}\right)}$

(2b) ${\displaystyle x_{2}=\cos \left({\frac {\alpha +2\pi }{3}}\right)+i\sin \left({\frac {\alpha +2\pi }{3}}\right)}$

(2c) ${\displaystyle x_{3}=\cos \left({\frac {\alpha +4\pi }{3}}\right)+i\sin \left({\frac {\alpha +4\pi }{3}}\right)}$

che nel piano di Gauss - Argand corrispondono ai vertici del triangolo equilatero inscritto nella circonferenza di raggio unitario che ha centro nell'origine degli assi.

L'equazione (1), dunque, è l'enunciato analitico della trisezione dell'angolo α. Se l'equazione (1) fosse riducibile allora dovrebbe essere possibile esprimere una sua radice come funzione razionale di ${\displaystyle \cos \alpha }$ e ${\displaystyle \sin \alpha ;}$ funzione che non si altererebbe mutando α in α + 2π. Al contrario, nessuna delle tre radici rimane inalterata quando, variando in modo continuo, α passa al valore α + 2π , poiché in tal caso x1 passa in x2, x2 a sua volta passa in x3 e x3 in x1 ovvero si ha una permutazione ciclica delle radici. Nessuna di esse, quindi, può essere rappresentata come una funzione razionale di ${\displaystyle \cos \alpha }$ e ${\displaystyle \sin \alpha ;}$ ma se questo è vero ne segue che l'equazione (1) è irriducibile.

C'è un'importante differenza tra il problema di trisecare un angolo e gli altri due problemi greci classici: non si può quadrare nessun cerchio con riga e compasso, non si può duplicare nessun cubo con riga e compasso, ma esistono alcuni angoli particolari, come quelli di 90°, 27° o 45°, per cui la trisezione è possibile con riga e compasso.

Costruzioni con riga e compasso

Come nacque il problema di riuscire a trisecare un angolo con riga e compasso? Esaminiamo la costruzione con riga e compasso per bisecare un angolo. La costruzione è diretta, come si vede nella figura: dato l'angolo CÂB individuiamo due lunghezze uguali ${\displaystyle AB}$ e ${\displaystyle AC}$ sui suoi lati. Costruiamo quindi il parallelogramma ${\displaystyle CABD}$ e disegniamo la diagonale ${\displaystyle AD}$ che biseca l'angolo CÂB.

Il metodo per bisecare l'angolo è dunque molto semplice. Gli antichi greci pensarono che fosse altrettanto semplice poter dividere gli angoli in ogni modo, cercarono quindi un metodo con riga e compasso che permettesse di dividere un angolo in tre parti uguali. Ben presto si accorsero che il problema era più difficoltoso: in effetti, il problema è risolvibile con riga e compasso solo per alcuni tipi di angoli, ma nel caso generale ciò non è possibile. Vediamo ora due esempi di trisezione possibili con riga e compasso.

Trisezione di un angolo retto e di un angolo di mπ/2^k

La trisezione, col solo uso di riga e compasso è possibile in alcuni casi particolari, ad esempio per un angolo retto. Infatti, dato un angolo retto (figura 2) si traccia una circonferenza Γ₁ con centro in ${\displaystyle A}$ e raggio ${\displaystyle r}$ qualsiasi; essa taglia la semiretta per ${\displaystyle A}$ in ${\displaystyle B}$. Ora si traccia la circonferenza Γ₂ con centro in ${\displaystyle B}$ e raggio ${\displaystyle r}$; essa intersecherà la circonferenza Γ₁ in ${\displaystyle D}$.

Il triangolo ${\displaystyle ABD}$ è equilatero; infatti ${\displaystyle AB=AD=BD=r}$. Quindi l'angolo BÂD = π/3 e, per differenza, l'angolo DÂC = π/6. Di conseguenza è possibile trisecare l'angolo CÂB.

Per trisecare un angolo di π/4 è sufficiente, dopo aver trisecato un angolo retto, bisecare l'angolo di π/6 che si ottiene.

Con questa tecnica si possono trisecare (col solo uso di riga e compasso) gli angoli la cui ampiezza sia:

${\displaystyle \varphi ={\frac {m\pi }{2^{k}}},\qquad k\in \mathbb {N} ,\,m\in \mathbb {Z} .}$

Trisezione con l'uso di una riga graduata

Il metodo di Nicomede

Quello di Nicomede non è propriamente un metodo di costruzione, perché egli usò la riga per riportare una lunghezza, ovvero utilizzò idealmente una riga graduata. Dato un angolo qualsiasi CÂB (vedere figura 4), si considera una retta ${\displaystyle d}$, perpendicolare ad ${\displaystyle AB}$, la quale intersechi ${\displaystyle AB}$ in ${\displaystyle D}$ e ${\displaystyle AC}$ in ${\displaystyle C}$; per ${\displaystyle C}$ si traccia una retta ${\displaystyle e}$ parallela ad ${\displaystyle AB}$ e per ${\displaystyle A}$ si traccia una retta ${\displaystyle f}$ parallela a ${\displaystyle d}$; le rette ${\displaystyle e}$ ed ${\displaystyle f}$ si intersechino in ${\displaystyle F}$. Ora per ${\displaystyle A}$ si traccia una retta ${\displaystyle g}$, la quale interseca ${\displaystyle d}$ in ${\displaystyle H}$ ed ${\displaystyle e}$ in ${\displaystyle E}$ in modo che:

${\displaystyle HE=2AC}$; allora EÂD = ${\displaystyle {1 \over 3}}$ CÂD.

• CD ${\displaystyle \perp }$ AB
• FE // AD
• FA // CD
• ${\displaystyle HE\cong 2AC}$

EÂD ${\displaystyle \cong {1 \over 3}}$ CÂD.

Detto ${\displaystyle G}$ il punto medio di ${\displaystyle HE}$, si ha:

(13) ${\displaystyle HG\cong GE}$ per costruzione

(14) ${\displaystyle CG\cong HG\cong GE}$ perché il triangolo ${\displaystyle CHE}$ è rettangolo.

Quindi è anche:

(15) ${\displaystyle AC\cong HG\cong CG\cong GE.}$

D'altra parte

(16) EÂB ${\displaystyle \cong }$ CÊG perché angoli alterni interni

(17) CÊG ${\displaystyle \cong }$ EĈG perché il triangolo ${\displaystyle CGE}$ è isoscele.

L'angolo CĜH è l'angolo esterno del triangolo ${\displaystyle CGE}$ e, quindi,

(18) CĜH ${\displaystyle \cong }$ EĈG + CÊG ${\displaystyle \cong }$ 2 CÊG

Ma anche

(19) CĜH ${\displaystyle \cong }$ CÂG perché il triangolo ${\displaystyle CAG}$ è isoscele.

Allora

(20) CÂB ${\displaystyle =}$ CÂG + GÂB ${\displaystyle \cong }$ 2 CÊG + GÂB ${\displaystyle \cong }$ 2 GÂB + GÂB ${\displaystyle =}$ 3 GÂB

Ossia

(21) GÂB ${\displaystyle \cong {\frac {1}{3}}}$ CÂB QED

Il metodo di Archimede

Nella soluzione proposta da Archimede la riga viene usata per riportare una lunghezza e, quindi, è pensata come riga graduata. Supponiamo di voler trisecare CÂB (vedi figura 5), disegniamo una circonferenza ${\displaystyle \Gamma }$, con centro in ${\displaystyle A}$ e raggio ${\displaystyle r}$, la quale interseca la semiretta ${\displaystyle c}$ in ${\displaystyle C}$ e la semiretta ${\displaystyle b}$ in ${\displaystyle B}$; per ${\displaystyle C}$ tracciamo una retta ${\displaystyle d}$ che taglia la retta ${\displaystyle b}$ nel punto ${\displaystyle E}$ e la circonferenza nel punto ${\displaystyle F}$ in modo tale che ${\displaystyle EF}$ sia congruente al raggio della circonferenza. Per ${\displaystyle A}$ tracciamo la retta e parallela a ${\displaystyle d}$, la quale interseca la circonferenza in ${\displaystyle X}$. L'angolo XÂB è la terza parte dell'angolo dato.

Hp: ${\displaystyle EF\cong AF\cong AB\cong AC}$

Th: XÂB ${\displaystyle \cong \left({\frac {1}{3}}\right)}$ CÂB

Dimostrazione

Si osservi che, per costruzione, i due triangoli ${\displaystyle EFA}$ e ${\displaystyle CAF}$ sono isosceli. In particolare il lato ${\displaystyle EF}$ è congruente al lato ${\displaystyle AF}$ perché si è presa la retta ${\displaystyle c}$ in modo tale che la distanza tra il punto di intersezione di tale retta con la retta ${\displaystyle b}$ e il punto di intersezione con la circonferenza fosse uguale al raggio; mentre il lato ${\displaystyle AF}$ è congruente al lato ${\displaystyle AC}$ perché entrambi raggi della stessa circonferenza.

Da ciò segue che

(22) FÊA ${\displaystyle \cong }$ FÂE,

(23) AĈF ${\displaystyle \cong }$ AFC.

Inoltre l'angolo CÂB è angolo esterno del triangolo ${\displaystyle EAC}$ e quindi

(24) CÂB ${\displaystyle \cong }$ FÊA + AĈF.

A sua volta AĈF è congruente all'angolo ${\displaystyle AFC}$, che è angolo esterno del triangolo ${\displaystyle EFA}$ e quindi

(25) AFC ${\displaystyle \cong }$ FÊA + FÂE ${\displaystyle \cong }$ 2 FÊA.

Unendo le relazioni (24) e (25) si ottiene

(26) CÂB ${\displaystyle \cong }$ FÊA +2 FÊA = 3 FÊA.

Ossia

(27) FÊA ${\displaystyle \cong {1 \over 3}}$ CÂB.

D'altronde EF // AX (tagliati dalla trasversale b) e gli angoli FÊA e XÂB sono angoli corrispondenti e dunque

(28) FÊA ${\displaystyle \cong }$ XÂB.

Confrontando le relazioni (27) e (28) si ricava

(29) XÂB ${\displaystyle \cong {1 \over 3}}$ CÂB.

c.v.d.

Soluzioni con l'utilizzo di coniche

Dalla morte di Apollonio avvenuta nel 190 a.C. circa, la geometria classica non aveva più trovato nessun sostenitore. Tuttavia, durante il regno di Diocleziano (284-305), visse ad Alessandria uno scienziato animato dallo spirito che aveva posseduto Euclide, Archimede e Apollonio: Pappo di Alessandria (290–350 d.C.) il quale, verso il 320 d.C. compose un'opera, in 8 libri, dal titolo Collezione matematica. Questa opera è molto importante in quanto ci fornisce una preziosa documentazione storica concernente alcuni aspetti della matematica greca che altrimenti sarebbero rimasti sconosciuti. La Collezione contiene anche dimostrazioni alternative e lemmi supplementari relativi a teoremi di Euclide, Archimede, Apollonio e Tolomeo. Infine, il trattato presenta nuove scoperte e generalizzazioni che non è dato trovare in nessuna opera precedente. Molto importante è il Libro III in cui Pappo fa una netta distinzione tra problemi "piani", "solidi" e "lineari": i primi sono costruibili solo con cerchi e rette, i secondi sono risolvibili mediante l'uso di sezioni coniche e l'ultimo genere di problemi richiede curve diverse da rette, cerchi e coniche. In particolar modo il problema della trisezione dell'angolo viene presentato come un problema del secondo tipo, cioè come un problema solido e lo stesso Pappo ne suggerisce alcuni metodi di risoluzione facendo uso di sezioni coniche. La Collezione matematica di Pappo è l'ultimo trattato matematico veramente significativo dell'antichità, poiché il tentativo da lui fatto di ridare alla geometria nuova vitalità non fu coronato dal successo. Si continuarono a scrivere opere matematiche in greco per un altro millennio circa, ma gli autori che vennero dopo Pappo non raggiunsero mai il suo livello. Le loro opere hanno quasi esclusivamente la forma di commento a trattati anteriori.

La soluzione di Pappo

Pappo risolve il problema della trisezione utilizzando le coniche ma rifacendosi a un'idea di Apollonio. L'idea da cui partì Pappo è la seguente: fissata una linea ${\displaystyle AB}$, si vuole determinare il luogo dei punti ${\displaystyle P}$ per i quali vale la seguente relazione: 2x PÂB = PBA.

Osserviamo le seguenti figure:

Si può dimostrare che tale luogo geometrico è un'iperbole avente eccentricità 2, un fuoco in ${\displaystyle B}$ e come direttrice l'asse del segmento ${\displaystyle AB}$ (vedere figura a sinistra). Considerando ${\displaystyle O}$ come centro, disegniamo un cerchio che passi per ${\displaystyle A}$ e per ${\displaystyle B;}$ se costruiamo un'iperbole con eccentricità 2, fuoco in ${\displaystyle B}$ e direttrice l'asse di ${\displaystyle AB}$, tale iperbole interseca il cerchio in ${\displaystyle P}$. Il segmento ${\displaystyle PO}$ triseca l'angolo AÔB. Per dimostrarlo notiamo che, dalle proprietà dell'iperbole descritta, 2x PÂB = PBA. Ma un angolo al centro è il doppio dell'angolo alla circonferenza che insiste sullo stesso arco quindi:

2x PÂB = PÔB (entrambi insistono sull'arco ${\displaystyle PB}$)

e

2x PBA = PÔA (entrambi insistono sull'arco ${\displaystyle PA}$).

Unendo le due relazioni si ottiene 2x PÔB = PÔA cioè l'angolo PÔB è la terza parte dell'angolo BÔA.

c.v.d.

Soluzione con l'utilizzo della concoide di Nicomede

Nicomede visse circa nello stesso periodo di Archimede (nel II secolo a.C.) e produsse la famosa curva concoide (conchiglia in greco).

Fissiamo un punto ${\displaystyle O}$ (detto polo) e una retta ${\displaystyle m}$ distante ${\displaystyle d}$ da ${\displaystyle O}$. Consideriamo una seconda retta passante per ${\displaystyle O}$, che interseca la retta ${\displaystyle m}$ in ${\displaystyle A}$. Su tale retta, da entrambe le parti rispetto ad ${\displaystyle A}$ stacchiamo due segmenti ${\displaystyle AP=AP'}$ ciascuno di lunghezza ${\displaystyle k}$. Il luogo dei punti ${\displaystyle P}$ e ${\displaystyle P'}$ ottenuti ruotando la retta per ${\displaystyle O}$ si chiama appunto concoide di Nicomede. La parte descritta dal punto più lontano ad ${\displaystyle O}$ (cioè ${\displaystyle P}$) si dice ramo esterno della concoide; l'altra parte ramo interno. Ponendo il punto ${\displaystyle O}$ nell'origine di un sistema di assi cartesiano ${\displaystyle xOy}$ e prendendo la retta m parallela all'asse ${\displaystyle y}$, avente quindi equazione ${\displaystyle x=a}$, l'equazione cartesiana della curva è:

${\displaystyle (x^{2}+y^{2})(x-d)^{2}=k^{2}x^{2}.}$

Se invece il sistema di riferimento è un sistema polare l'equazione diventa

${\displaystyle \rho ={\frac {d}{\cos \theta }}+k.}$

Le equazioni parametriche sono invece:

${\displaystyle {\begin{cases}x=d+k\cos \theta \\y=d\tan \theta +k\sin \theta .\end{cases}}}$

Trisezione dell'angolo

La curva può essere utilizzata per risolvere il problema della trisezione dell'angolo. Sia AÔB un angolo qualunque; da un punto arbitrario ${\displaystyle L}$ del lato ${\displaystyle OB}$ conduciamo la perpendicolare ${\displaystyle LD}$ al lato ${\displaystyle OA}$ e consideriamo la concoide della retta ${\displaystyle LD}$ rispetto al polo ${\displaystyle O}$ di costante ${\displaystyle k=2OL}$. La parallela ad ${\displaystyle OA}$, uscente da ${\displaystyle L}$ incontra il ramo esterno della concoide in ${\displaystyle C}$. Si congiunga ${\displaystyle C}$ con ${\displaystyle O}$ e dimostriamo che

AÔC = ${\displaystyle {1 \over 3}}$ AÔB.

Dimostrazione

Chiamiamo ${\displaystyle N}$ il punto d'intersezione di ${\displaystyle OC}$ con ${\displaystyle LD}$ ed ${\displaystyle M}$ il punto medio di ${\displaystyle CN}$. Per definizione di concoide, sarà:

${\displaystyle CN=k=2OL}$

e quindi

${\displaystyle CM=MN=OL={k \over 2}.}$

D'altra parte ${\displaystyle NLC}$ è un angolo retto, allora ${\displaystyle LM}$, come mediana relativa all'ipotenusa ${\displaystyle CN}$ del triangolo rettangolo ${\displaystyle CLN}$, è metà dell'ipotenusa stessa, cioè

LM = NM = OL.

Ne segue che i triangoli ${\displaystyle LOM}$, ${\displaystyle LMC}$ e ${\displaystyle LMN}$ sono isosceli e quindi:

LÔM = NML = 2 LĈM.

Ma LCM = COA perché alterni interni e perciò LÔM = 2 CÔA o anche

BÔA = LÔA = 3 CÔA.

c.v.d.

Soluzione con l'utilizzo della trisettrice di Mac Laurin

Questa curva fu studiata da Colin Maclaurin nel 1742. Come altre curve essa fornisce una soluzione al problema della trisezione. Il nome stesso trisettrice nasce appunto dal fatto che essa si può utilizzare per trisecare gli angoli. La trisettrice è una famiglia di curve algebriche di ordine 3, cioè di cubiche in particolare sono cubiche con un nodo; le tangenti in questo punto sono inclinate di ± 60° rispetto all'asse della curva. L'area del cappio vale e la distanza dell'origine dal punto in cui la curva taglia l'asse ${\displaystyle x}$ è ${\displaystyle 3a}$. La sua equazione cartesiana è

${\displaystyle y^{2}\left(a+x\right)=x^{2}\left(3a-x\right).}$

Le equazioni parametriche sono:

${\displaystyle \left\{{\begin{matrix}x=a{\frac {t^{2}-3}{t^{2}+1}}&{\mbox{ }}\\y=a{\frac {t\left(t^{2}-3\right)}{t^{2}+1}}&{\mbox{ }}\end{matrix}}\right.}$

Mentre l'equazione polare è la seguente:

${\displaystyle \rho ={\frac {2\alpha \sin \left(3\theta \right)}{\sin \left(2\theta \right)}}.}$

In figura è rappresentata la trisettrice di MacLaurin con nodo nell'origine e nei due casi ${\displaystyle a>0}$ (a sinistra) e ${\displaystyle a<0}$ (a destra).

Supponiamo di avere una trisettrice con nodo nell'origine che taglia l'asse ${\displaystyle x}$ nel punto ${\displaystyle (-3,0)}$, e sia ${\displaystyle P}$ un punto qualsiasi sul cappio della curva. L'angolo formato dai punti ${\displaystyle [(-3,0),(-2,0),P]}$ è il triplo dell'angolo formato dai punti ${\displaystyle [(-2,0),(0,0),P]}$.

Soluzione con l'utilizzo della chiocciola (o lumaca) di Pascal

Blaise Pascal, era un prodigio matematico. Anche suo padre aveva una notevole inclinazione per la matematica; la lumaca o chiocciola di Pascal prende appunto il nome dal padre Étienne Pascal, che la studiò. Questa curva era nota agli antichi come la concoide del cerchio, ma Etienne Pascal ne fece uno studio così approfondito che da allora prende il suo nome.

Consideriamo la curva luogo geometrico dei punti ${\displaystyle P}$ tali che dati due punti ${\displaystyle O}$ e ${\displaystyle A}$ nel triangolo ${\displaystyle AOP}$, l'angolo in ${\displaystyle O}$ sia doppio di quello in ${\displaystyle P}$. Poniamo gli assi cartesiani con l'origine in ${\displaystyle O}$ e il lato ${\displaystyle OA}$ del triangolo ${\displaystyle OAP}$ sull'asse delle ascisse. Dal centro tracciamo una retta qualsiasi inclinata di ${\displaystyle 2\alpha }$ e dal punto ${\displaystyle A}$ una retta inclinata di ${\displaystyle 3\alpha }$, punto comune a queste due rette è un punto ${\displaystyle P}$ del luogo geometrico cercato.

Conduciamo la bisettrice dell'angolo AÔB e sia ${\displaystyle H}$ il punto d'incontro della bisettrice con ${\displaystyle AP}$, si ha

OPA = α = HÔP = AÔH

e

OĤA = PÔA = 2α.

Perciò i due triangoli ${\displaystyle OAH}$ e ${\displaystyle PAO}$ sono simili, quindi:

${\displaystyle {\frac {OA}{AH}}={\frac {AP}{OA}}={\frac {PO}{HO}},}$

da cui

${\displaystyle AH={\frac {OA^{2}}{AP}}}$

${\displaystyle HP=OH={\frac {(AO)(PO)}{AP}}.}$

Quindi

${\displaystyle AH+HP=AP={\frac {OA^{2}}{AP}}+{\frac {(AO)(PO)}{AP}},}$

per cui

${\displaystyle AP^{2}=OA^{2}+OA\cdot OP}$

ed anche

${\displaystyle AP^{2}=OA(OA+OP).}$

Riferendoci alle coordinate abbiamo:

${\displaystyle \left(x-a\right)^{2}+y^{2}=a\left(a+{\sqrt {x^{2}+y^{2}}}\right)}$

${\displaystyle x^{2}+a^{2}-2ax+y^{2}=a^{2}+a{\sqrt {x^{2}+y^{2}}}}$

${\displaystyle \left(x^{2}+y^{2}-2ax\right)^{2}=a^{2}\left(x^{2}+y^{2}\right),}$

che è l'equazione cartesiana della chiocciola di Pascal. Quindi ne segue che PÂX = OPA.

Soluzione con l'utilizzo della spirale di Archimede

Archimede, come i suoi predecessori, fu attratto dai tre famosi problemi della geometria: la sua famosa spirale fornì la soluzione a due di questi problemi. La spirale viene definita come il luogo piano di un punto che, partendo dall'estremo di un raggio o semiretta, si sposta uniformemente lungo questo raggio mentre il raggio a sua volta ruota uniformemente intorno al suo estremo. Espressa in coordinate polari, l'equazione della spirale è

${\displaystyle r=a\theta .}$

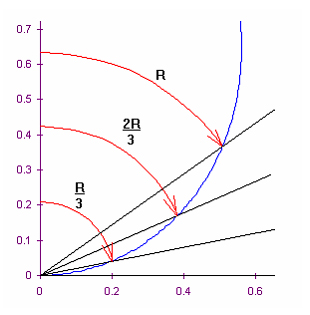
Data una spirale del genere viene facilmente effettuata la trisezione di un angolo. L'angolo è disposto in modo che il vertice e uno dei lati coincidano con il punto iniziale della spirale e con la posizione iniziale della semiretta che ruota. L'altro lato dell'angolo intersecherà la spirale in un punto che individua su questo lato un segmento lungo ${\displaystyle R}$ (vedi figura). Tracciamo la circonferenza con centro nell'origine e raggio uguale a ${\displaystyle R}$, tale circonferenza individua un segmento sull'asse delle ${\displaystyle y}$. Dividiamo in tre parti questo segmento e disegniamo archi di circonferenza con centro nell'origine e raggio pari a ${\displaystyle 2R/3}$ e ${\displaystyle R/3}$, tali archi intersecano la spirale in due punti che individuano le due linee che trisecano l'angolo di partenza. Con questo metodo ogni angolo può essere diviso in un numero qualsiasi di parti uguali.

Bibliografia

• (EN) Martin Gardner, How to Trisect an Angle, in Mathematical Carnival, 1992, pp. 255-265.

Altri progetti

• Wikimedia Commons contiene immagini o altri file su trisezione dell'angolo

Collegamenti esterni

• angolo, trisezione di un, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) trisecting the angle, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Trisezione dell'angolo, su MathWorld, Wolfram Research.
• (EN) Angle trisection by Archimedes of Syracuse
• (EN) Angle trisection da The Geometry Center

V · D · M Problemi classici della geometria greca
Trisezione dell'angolo · Quadratura del cerchio · Duplicazione del cubo

Controllo di autorità	LCCN (EN) sh85137916 · J9U (EN, HE) 987007551116505171