Superellisse

Questa voce o sezione sull'argomento matematica è priva o carente di note e riferimenti bibliografici puntuali.

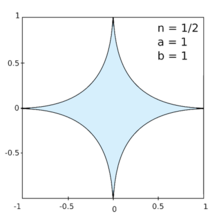
In geometria piana, per superellisse o curva di Lamé si intende una figura geometrica che generalizza l'ellisse. In un sistema di coordinate cartesiane viene descritto come il luogo dei punti (x, y) che soddisfano l'equazione

${\displaystyle \left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1}$ ,

con n, a e b reali positivi.

Nel caso n = 2 si ha l'ellisse ordinaria; è inoltre evidente che si tratta di insiemi di punti simmetrici rispetto agli assi Ox orizzontale e Oy verticale, e quindi anche rispetto al loro punto d'intersezione, O, origine del sistema di riferimento. Per n = 1 si ha un rombo con vertici (±a, 0) e (0, ±b).

Queste figure si possono ricondurre alle curve della famiglia indicizzata dal solo parametro n ottenibili fissando i valori a=b=1, cioè alle figure che soddisfano l'equazione normale

${\displaystyle \left|x\right|^{n}\!+\left|y\right|^{n}\!=1}$ ;

una superellisse della forma generale si ottiene applicando a quest'equazione le omotetie x → x/a e y → y/b.

Osservando le superellissi canoniche si vede che sono invarianti anche per le riflessioni rispetto alle rette per l'origine y = x e y = − x. Grazie all'invarianza per le riflessioni rispetto ai due assi, i punti di una superellisse si possono ripartire in 4 curve parziali, ciascuna appartenente ad un quadrante. Per studiare le superellissi dunque basta limitarsi al primo quadrante del piano cartesiano e considerare la curva data dalla funzione

${\displaystyle y\,=\,(1-x^{n})^{1/n}}$ .

Altra tipologia di superellisse è quella cuspidale o a "mandorla". Tale tipologia di ellisse possiede tutte le caratteristiche della superellisse classica, ma è discontinua ai vertici arrivando a possedere la caratteristica forma ad "occhio". Alla classe delle superellisse appartengono anche gli ellissoidi ovoidali dalla caratteristica forma ad uovo rappresentabili come delle curve quartiche. Quest'ultima tipologia di superellissi invece è discontinua solo in un punto.

Le figure della famiglia ottenute con n>2 sono dette iperellissi, quelle relative a n<2 sono chiamate ipoellissi. All'aumentare di n la curva canonica si avvicina sempre di più al rettangolo definito dai vertici opposti (1,1) e (-1,-1); al diminuire di n da 2 a 1 la curva da cerchio unitario si avvicina al quadrato definito dai vertici opposti (1,0) e (-1,0); al diminuire di n da 1 a 0 si hanno curve che si avvicinano alla croce formata dai due segmenti di lunghezza 2 con estremità in (-1,0) e (1,0) e con estremità (0,1) e (0,-1).

• (EN) Martin Gardner, Piet Hein's Superellipse, in Mathematical Carnival, 1992, pp. 240-254.
• Johan Gielis: Inventing the circle. The geometry of nature. - Antwerpen: Geniaal Press, 2003. - ISBN 9080775614
• Cresci Luciano: Le curve matematiche tra curiosità e divertimento - Hoepli 2005

• Superformula

• Wikimedia Commons contiene immagini o altri file su superellisse

• superellisse, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
• (EN) Eric W. Weisstein, Superellisse, su MathWorld, Wolfram Research.
• Lamé's Super Ellipse (Java-Applet), su activeart.de. URL consultato il 17 settembre 2004 (archiviato dall'url originale il 27 febbraio 2009).
• Super Ellipsoid (Java-Applet), su activeart.de. URL consultato il 17 settembre 2004 (archiviato dall'url originale il 24 maggio 2005).

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica