Figura replicante

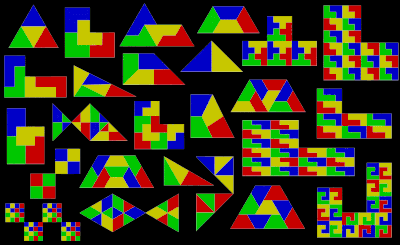
In geometria della tassellazione per figura replicante (o rettile^[1] dall'inglese rep-tile^[2]) si intende una figura autosimile, che si ripete^[3], per la proprietà di potersi scomporre in tasselli simili all'originale.

Terminologia

I tasselli replicanti furono chiamati "rettili", per via di un gioco di parole in inglese, dal matematico Solomon Golomb che per primo li studiò nel 1962. Una figura replicante è chiamata rep- $n$ se scomposta in $n$ copie uguali. Se invece la scomposizione è con forme simili non tutte uguali allora si parla di replicazione irregolare e di irrep-n^[4]. L'ordine di una forma replicante, che si utilizzino o meno tessere uguali, è il numero più piccolo possibile di tasselli utilizzato nella scomposizione.^[5]

Poligoni

Rep-2

Gli unici poligoni riproducibili di ordine 2 conosciuti sono il triangolo rettangolo isoscele e il parallelogramma le cui misure dei lati sono nel rapporto ${\sqrt {2}}$ . Le misure degli angoli interni del parallelogramma non influenzano questa proprietà. I formati della carta (A1,A2, A3, A4,...), utilizzati comunemente dalle nostre stampanti, utilizzano questa proprietà. I fogli di dimensioni diverse sono tutti simili e quindi, per esempio, dividendo in due un foglio A3 se ne ottengono due A4.

Rep-n

Analogamente a quanto visto precedentemente, nel caso particolare $n=2,$ dato un numero intero $n>1$ è possibile costruire un parallelogramma rep- $n$ . È infatti sufficiente costruire un parallelogramma con rapporto dei due lati ${\frac {a}{b}}={\sqrt {n}}$ e suddividere i suoi lati maggiori in $n$ parti uguali e poi congiungere gli opposti punti a due a due. Gli $n$ parallelogrammi così ottenuti avranno rapporto lati

{\frac {b}{a/n}}=n{\frac {b}{a}}={\frac {n}{\frac {a}{b}}}={\frac {n}{\sqrt {n}}}={\sqrt {n}}

e saranno perciò simili all'originale. Un rep- $n$ può essere frammentato all'infinito fino a formare un frattale, come per esempio il triangolo di Sierpinski

La sfinge è un tassello pentagonale replicante di ordine 4 che può presentarsi come rep-4 ma anche, frammentandosi, come rep-16, rep-64, irrep-13 etc.

Poligoni stellati

Un poligono stellato consiste in due o più poligono uniti da singoli punti.

Rep-4, monaco^[6]
Rep-9, pesce
Rep-8, pesce

Irrep-n

Un irrep-5 pentagonale
Un irrep-10 esagonale

Frattali

Tre figure di Golomb

Solomon Golomb ha individuato tre figure non poligonali rep-4 non costruibili in un numero finito di operazioni. Ognuna di esse è costituita da una diversa sovrapposizione di triangoli equilateri decrescenti in progressione geometrica di ragione ${\tfrac {1}{4}}$

Esempi

Il merletto di Koch è un esempio di replicante ordine 2, il triangolo di Sierpinski è invece di ordine 3, il tappeto di Sierpinski di ordine 8 e la spugna di Menger è un replicante di ordine 20.

Rep-3^[7]
Rep-5^[7]
Rep-7^[7]
Irrep-7, fiocco
Irrep- $\infty$ , siamese

Note

^ *Reptuile, in francese
^ *Rep-tile, piastrella replicante, in inglese "replicating tile", abbreviato in "rep-tile"
^ Gardner 1977.
^ (EN) Erich Friedman, Math Magic - Problem of the Month 10/2002, su erich-friedman.github.io, 2002. URL consultato il 1º dicembre 2023.
^ (EN) Martin Gardner, Rep-Tiles, in The Colossal Book of Mathematics: Classic Puzzles, Paradoxes, and Problems, New York, W. W. Norton, 2001, pp. 46–58, ISBN 9780393020236.
^ Giorgio Pietrocola, Mostra di rep-4, figure che si fanno in quattro per i figli, su Tartapelago, maecla.it, Maecla, 2009. URL consultato il 1º dicembre 2023.
^ ^a ^b ^c Mostra di rep-3, rep-5, rep-7 frattali che si fanno in tre, cinque e perfino in sette per la loro prole, su Tartapelago, maecla.it, Maecla, 2009. URL consultato il 1º dicembre 2023.

Bibliografia

Figure piane che si ripetono, in Enigmi e giochi matematici, vol. 4, Firenze, Sansoni, 1977, p. 205-217, OCLC 848765241.
(FR) Reptuile, su Dictionnaire de mathématiques récréatives, recreomath.qc.ca. URL consultato il 1º dicembre 2023.

Altri progetti

Wikimedia Commons

Wikimedia Commons contiene immagini o altri file su Figura replicante

Collegamenti esterni

(EN) Rep-tile, su Wolfram MathWorld, mathworld.wolfram.com. URL consultato il 1º dicembre 2023.
(EN) Irrep-tile, su Wolfram, demonstrations.wolfram.com. URL consultato il 1º dicembre 2023.
(EN) A.Vince, Self-Replicating Tiles and Their Boundary, su Geometric and computational geometry, researchgate.net, 1999. URL consultato il 1º dicembre 2023.