Determinante (algebra)

In algebra lineare, il determinante di una matrice quadrata è un numero che descrive alcune proprietà algebriche e geometriche della matrice. Si tratta di un potente strumento usato in vari settori della matematica, ad esempio nello studio dei sistemi di equazioni lineari, nel calcolo infinitesimale a più dimensioni (ad esempio nello Jacobiano), nel calcolo tensoriale, nella geometria differenziale, o nella teoria combinatoria.

Il significato geometrico principale del determinante si ottiene interpretando la matrice quadrata ${\displaystyle A}$ di ordine ${\displaystyle n}$ come trasformazione lineare di uno spazio vettoriale a ${\displaystyle n}$ dimensioni: con questa interpretazione, il valore assoluto di ${\displaystyle \det(A)}$ è il fattore con cui vengono modificati i volumi degli oggetti contenuti nello spazio (anche se ciò è improprio senza considerare il significato di misura). Se è diverso da zero, il segno del determinante indica inoltre se la trasformazione ${\displaystyle A}$ preserva o cambia l'orientazione dello spazio rispetto agli assi di riferimento.

Esso viene generalmente indicato con ${\displaystyle \det(A)}$ e, a volte, con ${\displaystyle |A|}$. Quest'ultima notazione è più compatta, ma anche più ambigua, in quanto utilizzata talvolta per descrivere una norma della matrice.^[1]

Definizione

Il determinante di una matrice 2 × 2 è pari a:

${\displaystyle \det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}=ad-bc.}$

Per definire il determinante di una generica matrice quadrata ${\displaystyle n\times n}$ si possono seguire due approcci: quello assiomatico, che definisce il determinante come l'unica quantità che soddisfa alcuni assiomi, e quello costruttivo tramite una formula esplicita. Esistono poi vari metodi di calcolo che risultano più agevoli a seconda del contesto.

Definizione tramite assiomi

Sia ${\displaystyle K^{n\times n}}$ lo spazio vettoriale delle matrici quadrate ${\displaystyle n\times n}$ a valori nel campo ${\displaystyle K}$ (ad esempio, il campo dei numeri reali o complessi).

Il determinante è l'unica funzione ${\displaystyle \det \colon K^{n\times n}\to K}$ avente le proprietà seguenti:

• ${\displaystyle \det I=1}$ dove la matrice ${\displaystyle I}$ è la matrice identità di ordine ${\displaystyle n}$.
• Si comporta nel modo seguente rispetto all'algoritmo di Gauss-Jordan:
  • se ${\displaystyle B}$ è ottenuta scambiando due righe o due colonne di ${\displaystyle A}$, allora ${\displaystyle \det B=-\det A;}$
  • se ${\displaystyle B}$ è ottenuta moltiplicando una riga o una colonna di ${\displaystyle A}$ per ${\displaystyle k\in K}$, allora ${\displaystyle \det B=k\det A;}$
  • se ${\displaystyle B}$ è ottenuta sommando un multiplo di una riga o di una colonna rispettivamente di ${\displaystyle A}$ a un'altra, allora ${\displaystyle \det B=\det A.}$

Le proprietà elencate hanno un significato geometrico: sono le proprietà che deve verificare una funzione il cui valore assoluto è il volume del poliedro individuato dai vettori riga della matrice ${\displaystyle B}$ e il cui segno è positivo se e solo se tali vettori sono equiorientati alla base canonica.

Definizione costruttiva

Il determinante di una matrice ${\displaystyle A_{n\times n}}$ può essere definito in un modo più costruttivo, tramite la formula di Leibniz:

${\displaystyle \det(A):=\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma (i)}.}$

Nella formula, ${\displaystyle S_{n}}$ è l'insieme di tutte le permutazioni ${\displaystyle \sigma }$ dell'insieme numerico ${\displaystyle \{1,2,\ldots ,n\}}$, ${\displaystyle \operatorname {sgn}(\sigma )}$ denota il segno della permutazione (${\displaystyle +1}$ se ${\displaystyle \sigma }$ è una permutazione pari, ${\displaystyle -1}$ se è dispari) e ${\displaystyle \sigma (i)}$ indica l'${\displaystyle i}$-esimo elemento della permutazione.

Da questa formula si vede che il numero di elementi della sommatoria è uguale a ${\displaystyle n!}$ (la cardinalità di ${\displaystyle S_{n}}$).

Per esempio, il determinante di una matrice ${\displaystyle 3\times 3}$ (cioè ${\displaystyle n=3}$) è

${\displaystyle {\begin{aligned}\sum _{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}a_{i,\sigma _{i}}&=\operatorname {sgn}([1,2,3])\prod _{i=1}^{n}a_{i,[1,2,3]_{i}}+\operatorname {sgn}([1,3,2])\prod _{i=1}^{n}a_{i,[1,3,2]_{i}}+\operatorname {sgn}([2,1,3])\prod _{i=1}^{n}a_{i,[2,1,3]_{i}}+\operatorname {sgn}([2,3,1])\prod _{i=1}^{n}a_{i,[2,3,1]_{i}}+\operatorname {sgn}([3,1,2])\prod _{i=1}^{n}a_{i,[3,1,2]_{i}}+\operatorname {sgn}([3,2,1])\prod _{i=1}^{n}a_{i,[3,2,1]_{i}}\\&=\prod _{i=1}^{n}a_{i,[1,2,3]_{i}}-\prod _{i=1}^{n}a_{i,[1,3,2]_{i}}-\prod _{i=1}^{n}a_{i,[2,1,3]_{i}}+\prod _{i=1}^{n}a_{i,[2,3,1]_{i}}+\prod _{i=1}^{n}a_{i,[3,1,2]_{i}}-\prod _{i=1}^{n}a_{i,[3,2,1]_{i}}\\&=a_{1,1}a_{2,2}a_{3,3}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}+a_{1,2}a_{2,3}a_{3,1}+a_{1,3}a_{2,1}a_{3,2}-a_{1,3}a_{2,2}a_{3,1}.\end{aligned}}}$

In particolare:

• Se ${\displaystyle n=1}$, il determinante di ${\displaystyle A}$ è semplicemente:

${\displaystyle \det(A):=a_{1,1}.}$

• Se ${\displaystyle n=2}$, si ottiene la formula già vista:

${\displaystyle \det(A):=a_{1,1}a_{2,2}-a_{2,1}a_{1,2}.}$

• Se ${\displaystyle n=3}$, si ottiene:

${\displaystyle \det(A):=a_{1,1}a_{2,2}a_{3,3}+a_{1,3}a_{2,1}a_{3,2}+a_{1,2}a_{2,3}a_{3,1}-a_{1,3}a_{2,2}a_{3,1}-a_{1,1}a_{2,3}a_{3,2}-a_{1,2}a_{2,1}a_{3,3}.}$

Quest'ultima formula può essere memorizzata tramite la regola di Sarrus (che non è però estendibile ai casi ${\displaystyle n>3}$).

La complessità della definizione costruttiva (comprese la generazione delle permutazioni) è elevata:

${\displaystyle n!\cdot (2n+1)=O(N\cdot N!).}$

Metodi di calcolo

La definizione costruttiva del determinante è spesso complicata da usare per un calcolo concreto, perché si basa su una somma di ben ${\displaystyle n!}$ addendi. Esistono altri algoritmi che consentono di calcolare il determinante più facilmente. Ciascun metodo ha una efficienza variabile, dipendente dalla grandezza della matrice e dalla presenza di zeri.

Matrici quadrate di ordine 2

Il determinante di una matrice 2 × 2 è:

${\displaystyle \det {\begin{pmatrix}a&b\\c&d\end{pmatrix}}:=ad-bc.}$

Il valore assoluto di questa espressione è uguale all'area del parallelogramma con vertici in ${\displaystyle (0,0),(a,c),(b,d)}$ e ${\displaystyle (a+b,c+d)}$. Il segno del determinante (se diverso da zero) dipende invece dall'ordine ciclico con cui compaiono i vertici del parallelogramma (il segno è negativo se il parallelogramma è stato "ribaltato", e positivo altrimenti).

Come spiegato più sotto, questa proprietà geometrica si estende anche in dimensioni maggiori di 2: il determinante di una matrice ${\displaystyle 3\times 3}$ è ad esempio il volume del poliedro i cui vertici si ricavano dalle colonne della matrice con lo stesso procedimento visto.

Matrici quadrate di ordine 3

Il determinante di una matrice 3 × 3 è:

${\displaystyle \det {\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}=aei+bfg+cdh-gec-hfa-idb.}$

Un metodo mnemonico per ricordare questa formula, espresso dalla regola di Sarrus (questo metodo non si estende a matrici più grandi), prevede di calcolare i prodotti dei termini sulle diagonali "continue". Ripetendo a destra della matrice le sue prime due colonne:

${\displaystyle {\begin{pmatrix}a&b&c\\d&e&f\\g&h&i\end{pmatrix}}{\begin{matrix}a&b\\d&e\\g&h\end{matrix}}}$

I prodotti delle componenti sulle 3 "diagonali" che partono dall'alto a sinistra (diagonali principali) sono ${\displaystyle aei}$, ${\displaystyle bfg}$ e ${\displaystyle cdh}$, mentre sulle 3 "diagonali" che partono dal basso a sinistra (diagonali secondarie) si trovano ${\displaystyle gec}$, ${\displaystyle hfa}$, ${\displaystyle idb}$. Il determinante della matrice è esattamente la differenza tra la somma dei primi tre termini ${\displaystyle (aei+bfg+cdh)}$ e la somma degli ultimi tre ${\displaystyle (gec+hfa+idb)}$.

Notare che il valore del determinante equivale in questo caso al prodotto misto tra i vettori:

${\displaystyle {\begin{pmatrix}a\\d\\g\end{pmatrix}},\quad {\begin{pmatrix}b\\e\\h\end{pmatrix}},\quad {\begin{pmatrix}c\\f\\i\end{pmatrix}}.}$

e il suo valore assoluto è uguale al volume del parallelepipedo che ha i tre vettori come spigoli.

Sviluppo di Laplace

Lo sviluppo di Laplace è un metodo di calcolo del determinante, che risulta efficiente solo per matrici molto piccole o contenenti un gran numero di zeri^[2]. Si procede scegliendo una riga, la ${\displaystyle i}$-esima, tramite la formula:

${\displaystyle \det(A)=\sum _{j=1}^{n}\ a_{i,j}C_{i,j},}$

dove ${\displaystyle C_{i,j}}$ è il complemento algebrico della coppia ${\displaystyle (i,j)}$, cioè ${\displaystyle C_{i,j}}$ è data da ${\displaystyle (-1)^{i+j}}$ per il determinante (minore) di ordine ${\displaystyle n-1}$ ottenuto dalla matrice ${\displaystyle A}$ eliminando la riga ${\displaystyle i}$-esima e la colonna ${\displaystyle j}$-esima.

Esiste uno sviluppo analogo anche lungo la ${\displaystyle j}$-esima colonna.

Algoritmo di Gauss

La definizione assiomatica fornisce un altro utile strumento di calcolo del determinante, che si basa su questi due principi:

• Il determinante di una matrice triangolare è semplicemente il prodotto degli elementi sulla diagonale, cioè:

${\displaystyle \det(A)=\prod _{i=1}^{n}a_{ii}.}$

• Usando l'algoritmo di Gauss, è possibile trasformare ogni matrice in una matrice triangolare attraverso operazioni elementari su righe e colonne della stessa ; il cui effetto sul determinante è prescritto dagli assiomi.

Esempio

Supponiamo di voler calcolare il determinante di:

${\displaystyle A={\begin{pmatrix}-2&2&-3\\-1&1&3\\2&0&-1\end{pmatrix}}.}$

Si può procedere direttamente tramite la definizione costruttiva:

${\displaystyle {\begin{aligned}\det(A)&=(-2)\cdot 1\cdot (-1)+(-3)\cdot 0\cdot (-1)+2\cdot 3\cdot 2-(-3)\cdot 1\cdot 2-(-2)\cdot 3\cdot 0-2\cdot (-1)\cdot (-1)\\&=2+0+12-(-6)-0-2=18.\end{aligned}}}$

Alternativamente si può utilizzare lo sviluppo di Laplace secondo una riga o una colonna. Conviene scegliere una riga o una colonna con molti zeri, in modo da ridurre gli addendi dello sviluppo; nel nostro caso sviluppiamo secondo la seconda colonna:

${\displaystyle {\begin{aligned}\det(A)&=(-1)^{1+2}\cdot 2\cdot \det {\begin{pmatrix}-1&3\\2&-1\end{pmatrix}}+(-1)^{2+2}\cdot 1\cdot \det {\begin{pmatrix}-2&-3\\2&-1\end{pmatrix}}\\&=(-2)\cdot ((-1)\cdot (-1)-2\cdot 3)+1\cdot ((-2)\cdot (-1)-2\cdot (-3))=(-2)(-5)+8=18.\end{aligned}}}$

Lo sviluppo di Laplace può essere combinato con alcune mosse di Gauss. Ad esempio qui risulta particolarmente vantaggioso sommare la seconda colonna alla prima:

${\displaystyle {\begin{pmatrix}0&2&-3\\0&1&3\\2&0&-1\end{pmatrix}}.}$

Questa mossa non cambia il determinante. Sviluppando lungo la prima colonna si ottiene quindi ancora:

${\displaystyle \det(A)=(-1)^{3+1}\cdot 2\cdot \det {\begin{pmatrix}2&-3\\1&3\end{pmatrix}}=2\cdot (2\cdot 3-1\cdot (-3))=2\cdot 9=18.}$

Proprietà

Proprietà elementari

Dalle proprietà elencate nella definizione assiomatica, è facile dedurre che:

• Se tutti gli elementi di una riga (o colonna) sono nulli, allora ${\displaystyle \det(A)=0.}$
• Se ${\displaystyle A}$ ha due righe (o colonne) eguali, o proporzionali, allora ${\displaystyle \det(A)=0.}$
• Se una riga (o colonna) è combinazione lineare di due o più altre righe (o colonne) a essa parallele, allora ${\displaystyle \det(A)=0.}$
• Se ${\displaystyle A}$ viene modificata tramite mosse di Gauss sulle colonne (invece che sulle righe), l'effetto è sempre quello descritto nella definizione assiomatica.
• In particolare, scambiando tra di loro due righe o due colonne il determinante cambia segno, restando uguale in valore assoluto. Ne consegue che un numero pari di scambi non varia né il segno né il modulo del determinante.
• Se una riga (o una colonna) è somma di due righe (o colonne), ${\displaystyle \det(A)}$ è la somma dei due determinanti che si ottengono sostituendo a quella riga (o colonna) rispettivamente le due righe (o colonne) di cui è somma.

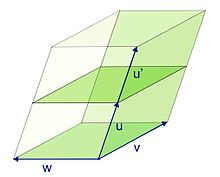
Moltiplicazione di matrici

Il determinante è una funzione moltiplicativa, nel senso che vale il teorema di Binet:

${\displaystyle \det(AB)=\det(A)\det(B).}$

Una matrice quadrata ${\displaystyle A}$ con valori in un campo ${\displaystyle K}$ è invertibile se e solo se ${\displaystyle \det(A)\neq 0}$. In caso affermativo vale l'uguaglianza:

${\displaystyle \det(A^{-1})=\det(A)^{-1}.}$

Le proprietà appena elencate mostrano che l'applicazione:

${\displaystyle \det \colon \mathrm {GL} _{n}(K)\to K^{*}}$

dal gruppo generale lineare negli elementi non nulli di ${\displaystyle K}$ è un omomorfismo di gruppi.

Come conseguenza del teorema di Binet, se ${\displaystyle I}$ è la matrice identità di tipo ${\displaystyle n\times n}$ e ${\displaystyle r}$ uno scalare, è facile verificare che ${\displaystyle \det(rI)=r^{n}}$. Infatti:

${\displaystyle \det(rA)=\det(rI\cdot A)=r^{n}\det(A).}$

Trasposte, matrici simili

Una matrice e la sua trasposta hanno lo stesso determinante:

${\displaystyle \det(A)=\det(A^{T}).}$

Se ${\displaystyle A}$ e ${\displaystyle B}$ sono simili (cioè esiste una matrice invertibile ${\displaystyle X}$ tale che ${\displaystyle A=X^{-1}BX}$) allora per il teorema di Binet ${\displaystyle \det(A)=\det(B)}$

Questo significa che il determinante è un invariante per similitudine. Da questo segue che il determinante di una trasformazione lineare ${\displaystyle f\colon V\to V}$ è ben definito (non dipende dalla scelta di una base per lo spazio vettoriale ${\displaystyle V}$).

D'altra parte, esistono matrici con lo stesso determinante che non sono simili.

Nel campo dei numeri reali, il segno del determinante è anche invariante per congruenza.

Autovalori

Il determinante di una matrice triangolare è il prodotto degli elementi nella diagonale.

Se ${\displaystyle A}$ è di tipo ${\displaystyle n\times n}$ con valori reali o complessi e ha tutti gli autovalori ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ nel campo (contati con molteplicità), allora:

${\displaystyle \det(A)=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

Questa uguaglianza segue dal fatto che ${\displaystyle A}$ è sempre simile alla sua forma normale di Jordan, che è una matrice triangolare superiore con gli autovalori sulla diagonale principale.

Dal collegamento fra determinante e autovalori si può derivare una relazione fra la funzione traccia, la funzione esponenziale e il determinante:

${\displaystyle \det(e^{A})=e^{\operatorname {tr} (A)}.}$

Derivata

Il determinante può considerarsi una funzione polinomiale:

${\displaystyle \det \colon \mathbb {R} ^{n\times n}\to \mathbb {R} ,}$

quindi essa è differenziabile rispetto a ogni variabile corrispondente al valore che può assumere in una casella e per qualunque suo valore. Il suo differenziale può essere espresso mediante la formula di Jacobi:

${\displaystyle d\det(A)=\operatorname {tr} (\operatorname {cof^{T}} (A)dA),}$

dove ${\displaystyle \operatorname {cof^{T}} (A)}$ denota la trasposta della matrice dei cofattori (detta anche dei complementi algebrici) di ${\displaystyle A}$, mentre ${\displaystyle \operatorname {tr} (A)}$ ne denota la traccia. In particolare, se ${\displaystyle A}$ è invertibile si ha:

${\displaystyle d\det(A)=\det(A)\operatorname {tr} (A^{-1}dA),}$

o, più colloquialmente, se i valori della matrice ${\displaystyle X}$ sono sufficientemente piccoli:

${\displaystyle \det(A+X)-\det(A)\approx \det(A)\operatorname {tr} (A^{-1}X).}$

Il caso particolare di ${\displaystyle A}$ coincidente con la matrice identità ${\displaystyle I}$ comporta:

${\displaystyle \det(I+X)\approx 1+\operatorname {tr} (X).}$

Applicazioni

Sistemi lineari

Il determinante è utile a calcolare il rango di una matrice e quindi a determinare se un sistema di equazioni lineari ha soluzione, tramite il teorema di Rouché-Capelli. Quando il sistema ha una sola soluzione, questa può essere esplicitata usando il determinante, mediante la regola di Cramer.

Matrici e trasformazioni invertibili

Una matrice è detta singolare se ha determinante nullo. Una matrice singolare non è mai invertibile, e se è definita su un campo vale anche l'inverso: una matrice non singolare è sempre invertibile.

Una trasformazione lineare del piano, dello spazio, o più in generale di uno spazio euclideo o vettoriale (di dimensione finita) ${\displaystyle f\colon V\to V}$ è rappresentata (dopo aver scelto una base) da una matrice quadrata ${\displaystyle A.}$ Il determinante è una quantità che non dipende dalla base scelta, e quindi solo dalla funzione ${\displaystyle f}$: si può quindi parlare di determinante di ${\displaystyle f}$, che si indica con ${\displaystyle \det(f)}$.

Le seguenti affermazioni su ${\displaystyle f}$ sono equivalenti:

${\displaystyle f}$ è una corrispondenza biunivoca ${\displaystyle \Leftrightarrow }$ ${\displaystyle f}$ è un isomorfismo ${\displaystyle \Leftrightarrow }$ ${\displaystyle f}$ è iniettiva ${\displaystyle \Leftrightarrow }$ ${\displaystyle f}$ è suriettiva ${\displaystyle \Leftrightarrow }$ ${\displaystyle \det(A)=\det(f)\neq 0.}$

Quindi ciascuna di queste affermazioni equivalenti è vera se e solo se il determinante non è zero.

Autovalori e autovettori

Il determinante consente di trovare gli autovalori di una matrice quadrata ${\displaystyle A}$ mediante il suo polinomio caratteristico:

${\displaystyle p(x)=\det(A-xI),}$

dove ${\displaystyle I}$ è la matrice identità avente stesso ordine di ${\displaystyle A.}$

Basi, sistemi di riferimento

Dati ${\displaystyle n}$ vettori nello spazio euclideo ${\displaystyle \mathbb {R} ^{n}}$, sia ${\displaystyle A}$ la matrice avente come colonne questi vettori. Le seguenti affermazioni sono equivalenti:

i vettori sono indipendenti ${\displaystyle \Leftrightarrow }$ i vettori generano ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \Leftrightarrow }$ i vettori formano una base ${\displaystyle \Leftrightarrow }$ ${\displaystyle \det(A)\neq 0.}$

Se gli ${\displaystyle n}$ vettori formano una base, allora il segno di ${\displaystyle \det(A)}$ determina l'orientazione della base: se positivo, la base forma un sistema di riferimento destrorso, mentre se è negativo si parla di sistema di riferimento sinistrorso (in analogia con la regola della mano destra).

Volumi

Il valore assoluto ${\displaystyle |\det A|}$ del determinante è uguale al volume del parallelepipedo sotteso dai vettori dati dalle colonne di ${\displaystyle A}$ (il parallelepipedo è in realtà un parallelogramma se ${\displaystyle n=2}$, e un solido di dimensione ${\displaystyle n}$ in generale). Più in generale, data una trasformazione lineare:

${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{n}}$

rappresentata da una matrice ${\displaystyle A}$, e un qualsiasi sottoinsieme ${\displaystyle S}$ di ${\displaystyle \mathbb {R} ^{n}}$ misurabile secondo Lebesgue, il volume dell'immagine ${\displaystyle f(S)}$ è dato da:

${\displaystyle \left|\det(A)\right|\cdot \operatorname {volume} (S).}$

Ancora più in generale, se la trasformazione lineare ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} ^{m}}$ è rappresentata da una matrice ${\displaystyle A}$ di tipo ${\displaystyle m\times n}$ e ${\displaystyle S}$ è un sottoinsieme di ${\displaystyle \mathbb {R} ^{n}}$ misurabile secondo Lebesgue, allora il volume di ${\displaystyle f(S)}$ è dato da:

${\displaystyle {\sqrt {\det(A^{T}A)}}\cdot \operatorname {volume} (S).}$

Generalizzazioni

Pfaffiano

Lo pfaffiano è un analogo del determinante per matrici antisimmetriche di tipo ${\displaystyle 2n\times 2n.}$ Si tratta di un polinomio di grado ${\displaystyle n}$ il cui quadrato è uguale al determinante della matrice.

Infinite dimensioni

Per gli spazi a infinite dimensioni non si trova alcuna generalizzazione dei determinanti e della nozione di volume. Sono possibili svariati approcci, inclusa la utilizzazione dell'estensione della traccia di una matrice.

Determinante di un endomorfismo

Se ${\displaystyle V}$ è uno spazio vettoriale di dimensione finita ${\displaystyle n}$ sul campo ${\displaystyle \mathbb {K} ,}$ allora è possibile definire il determinante di un endomorfismo ${\displaystyle f\colon V\to V}$ direttamente, senza fare ricorso a una base di ${\displaystyle V}$. Sia ${\displaystyle \Lambda ^{n}(V)}$ lo spazio vettoriale degli ${\displaystyle n-}$vettori di ${\displaystyle V}$. Consideriamo l'endomorfismo ${\displaystyle T_{f}}$ di ${\displaystyle \Lambda ^{n}(V)}$ definito di modo che:

${\displaystyle T_{f}(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})=f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n}),}$

per ogni ${\displaystyle x_{1},x_{2},\ldots ,x_{n}\in V}$, ed esteso per linearità a tutto ${\displaystyle \Lambda ^{n}(V)}$. Poiché ${\displaystyle \Lambda ^{n}(V)}$ ha dimensione uguale a 1 risulta che ${\displaystyle T_{f}}$ altro non è che la moltiplicazione per uno scalare. Quindi possiamo definire il determinante di ${\displaystyle f}$ attraverso l'equazione:

${\displaystyle f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})=\det(f)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n}),}$

per ogni ${\displaystyle x_{1},x_{2},\ldots ,x_{n}\in V}$. A questo punto seguono tutte le proprietà del determinante, in particolare è immediato che ${\displaystyle \det(\operatorname {id} )=1}$ dove ${\displaystyle \operatorname {id} }$ è l'endomorfismo identità di ${\displaystyle V}$. Se ${\displaystyle g}$ è un altro endomorfismo di ${\displaystyle V,}$ allora:

${\displaystyle {\begin{aligned}\det(g\circ f)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n})&=(g\circ f)(x_{1})\wedge (g\circ f)(x_{2})\wedge \cdots \wedge (g\circ f)(x_{n})\\&=\det(g)(f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n}))=\det(f)\det(g)(x_{1}\wedge x_{2}\wedge \cdots \wedge x_{n}),\end{aligned}}}$

da cui ${\displaystyle \det(g\circ f)=\det(g)\det(f)}$. Se ${\displaystyle f}$ non è un isomorfismo allora l'immagine di ${\displaystyle f}$ ha dimensione strettamente minore di ${\displaystyle n}$ e quindi ${\displaystyle f(x_{1}),f(x_{2}),\ldots ,f(x_{n})}$ sono sicuramente linearmente dipendenti, essendo che ${\displaystyle \wedge }$ è una forma multilineare alternante segue che ${\displaystyle f(x_{1})\wedge f(x_{2})\wedge \cdots \wedge f(x_{n})=0}$ e quindi ${\displaystyle \det(f)=0}$. Si verifica che fissata una base su ${\displaystyle V}$ il determinante della matrice associata a ${\displaystyle f}$ rispetto a tale base coincide con il determinante di ${\displaystyle f}$.

Storia

Note

Bibliografia

• (EN) Andrews, G. E. and Burge, W. H. Determinant Identities. Pacific J. Math. 158, 1-14, 1993.
• (EN) Arfken, G. "Determinants." §4.1 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 168–176, 1985.
• (EN) Brenner, J. and Cummings, L. The Hadamard Maximum Determinant Problem. Amer. Math. Monthly 79, 626-630, 1972.
• Ernesto Pascal I determinanti: teoria ed applicazioni. Con tutte le più recenti ricerche (Milano: U. Hoepli, 1897)
• Francesco Caldarera Trattato dei determinanti, in UniPI - Biblioteca Matematica Informatica Fisica (Palermo: Virzì, 1913)
• (FR) Francesco Brioschi, Théorie des déterminants et leurs principales applications; traduit de l'italien par M. Édouard Combescure, Parigi, Mallet-Bachelier, 1856. URL consultato il 25 luglio 2021.
• (FR) R. Baltzer, Théorie et applications des déterminants, avec l'indication des sources originales; traduit de l'allemand par J. Hoüel, Parigi, Mallet-Bachelier, 1861. URL consultato il 25 luglio 2021.
• (EN) Charles Dodgson An elementary treatise on determinants, with their application to simultaneous linear equations and algebraical geometry (Oxford: University Press, 1867)
• (EN) R. F. Scott e G. B. Matthews The theory of determinants and their applications (Cambridge: University Press, 1904)

Voci correlate

• Matrice jacobiana
• Matrice unimodulare
• Metodo di eliminazione di Gauss
• Permanente (matematica)
• Polinomio caratteristico
• Regola di Sarrus
• Teorema di Laplace

Altri progetti

• Wikizionario contiene il lemma di dizionario «determinante»
• Wikiversità contiene risorse sul determinante
• Wikimedia Commons contiene immagini o altri file sul determinante

Collegamenti esterni

• (EN) determinant, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Determinante, su MathWorld, Wolfram Research.
• (EN) Determinante, su Encyclopaedia of Mathematics, Springer e European Mathematical Society.
• (EN) Storia dell'uso delle matrici e dei determinanti su MacTutor
• (IT) Calcolatrice per matrici e vettori online
• (EN) WebApp to calculate determinants and descriptively solve systems of linear equations, su sole.ooz.ie. URL consultato il 19 gennaio 2014 (archiviato dall'url originale il 21 febbraio 2014).
• (EN) Determinant Interactive Program and Tutorial, su people.revoledu.com.
• (EN) Online Matrix Calculator, su matrixcalc.org.
• Calcolatore dei determinanti della matrice, su physandmathsolutions.com.
• (EN) Linear algebra: determinants. Archiviato il 4 dicembre 2008 in Internet Archive. Compute determinants of matrices up to order 6 using Laplace expansion you choose.
• (EN) Matrices and Linear Algebra on the Earliest Uses Pages, su economics.soton.ac.uk.
• (EN) Determinants explained in an easy fashion in the 4th chapter as a part of a Linear Algebra course., su algebra.math.ust.hk. URL consultato il 19 gennaio 2014 (archiviato dall'url originale il 25 maggio 2009).
• (EN) Instructional Video on taking the determinant of an nxn matrix (Khan Academy), su khanexercises.appspot.com (archiviato dall'url originale il 25 marzo 2010).

V · D · M Algebra lineare
Spazio vettoriale	Vettore · Sottospazio vettoriale (Sottospazio generato) · Applicazione lineare (Nucleo · Immagine) · Base · Dimensione · Teorema della dimensione · Formula di Grassmann · Sistema lineare · Algoritmo di Gauss · Teorema di Rouché-Capelli · Regola di Cramer · Spazio duale · Spazio proiettivo · Spazio affine · Teorema della dimensione per spazi vettoriali
Matrici	Identità · Nulla · Quadrata · Invertibile · Simmetrica · Antisimmetrica · Trasposta · Diagonale · Triangolare · Di cambiamento di base · Ortogonale · Normale · Simplettica · Moltiplicazione di matrici · Rango · Teorema di Kronecker · Minore · Matrice dei cofattori · Determinante · Teorema di Binet · Teorema di Laplace · Radice quadrata di una matrice
Diagonalizzabilità	Autovettore e autovalore · Spettro · Polinomio caratteristico · Polinomio minimo · Teorema di Hamilton-Cayley · Matrice a blocchi · Forma canonica di Jordan · Teorema di diagonalizzabilità
Prodotto scalare	Forma bilineare · Sottospazio ortogonale · Spazio euclideo · Base ortonormale · Algoritmo di Lagrange · Segnatura · Teorema di Sylvester · Gram-Schmidt · Forma sesquilineare · Forma hermitiana · Teorema spettrale

Controllo di autorità	Thesaurus BNCF 32649 · LCCN (EN) sh85037299 · GND (DE) 4138983-9 · BNF (FR) cb11975737s (data) · J9U (EN, HE) 987007550422505171 · NDL (EN, JA) 00562696