Fungsi phi Euler

Dalam teori bilangan, fungsi phi Euler (bahasa Inggris: Euler's totient function) adalah fungsi yang menghitung bilangan bulat positif hingga diberikan bilangan bulat ${\displaystyle n}$ yang prima nisbi dengan ${\displaystyle n}$. Fungsi ini ditulis dengan menggunakan huruf Yunani, phi, yang dilambangkan sebagai ${\displaystyle \varphi (m)}$ atau ${\displaystyle \phi (m)}$ menyatakan kardinal himpunan bilangan asli ${\displaystyle 1\leq n\leq m}$ dimana ${\displaystyle \gcd(m,n)=1}$.

Bilangan bulat positif yang < 9 adalah 1, 2, 3, 4, 5, 6, 7, 8. Diantara bilangan-bilangan tersebut yang saling prima terhadap 9 adalah 1, 2, 4, 5, 7, 8, maka banyaknya bilangan yang saling prima terhadap 9 adalah sebanyak 6 sehingga φ(9) = 6.

Fungsi ini dikemukakan oleh Leonhard Euler (L. 15 April 1707, Swiss. w. 18 September 1783, Rusia).

Identitas

Terdapat beberapa identitas mengenai fungsi Euler phi, diantaranya:

• ${\displaystyle \varphi (1)=0}$, ${\displaystyle \varphi (2)=1}$
• ${\displaystyle \varphi (p)=p-1}$, untuk ${\displaystyle p}$ adalah bilangan prima

• ${\displaystyle \varphi (mn)=\varphi (m)\varphi (n)}$ jika ${\displaystyle \gcd(m,n)=1}$
• ${\displaystyle \varphi (p^{n})=p^{n-1}(p-1)}$
• ${\displaystyle \varphi \left(\prod _{i=1}^{n}p_{i}\right)=\prod _{i=1}^{n}\left(p_{i}-1\right)}$

Rumus lainnya

Apabila rumus lain mengenai fungsi Euler phi, diantaranya

• ${\displaystyle a\mid b\implies \varphi (a)\mid \varphi (b)}$
• ${\displaystyle n\mid \varphi (a^{n}-1)}$, untuk setiap ${\displaystyle a,n>1}$
• ${\displaystyle \varphi (m,n)=\varphi (m)\cdot \varphi (n)}$

Perhatikan kasus khusus

• ${\displaystyle \varphi (2m)={\begin{cases}2\varphi (m)&{\text{ jika }}m{\text{ adalah genap}}\\\varphi (m)&{\text{ jika }}m{\text{ adalah ganjil}}\end{cases}}}$
• ${\displaystyle \varphi \left(n^{m}\right)=n^{m-1}\varphi (n)}$
• ${\displaystyle \varphi (\operatorname {lcm} (m,n))\cdot \varphi (\operatorname {gcd} (m,n))=\varphi (m)\cdot \varphi (n)}$ Bandingkan dengan rumus
• ${\displaystyle \operatorname {lcm} (m,n)\cdot \operatorname {gcd} (m,n)=m\cdot n}$

(Lihat kelipatan persekutuan terkecil.)

• φ(n) genap untuk n ≥ 3. Selain itu, jika n memiliki r faktor prima ganjil yang berbeda, 2^r | φ(n)
• Untuk a > 1 dan n > 6 sehingga 4 ∤ n terdapat l ≥ 2n sedemikian sehingga l | φ(aⁿ − 1).
• ${\displaystyle {\frac {\varphi (n)}{n}}={\frac {\varphi (\operatorname {rad} (n))}{\operatorname {rad} (n)}}}$

di mana ${\displaystyle \operatorname {rad} (n)}$ adalah radikal dari ${\displaystyle n}$.

• ${\displaystyle \sum _{d\mid n}{\frac {\mu ^{2}(d)}{\varphi (d)}}={\frac {n}{\varphi (n)}}}$ ^[2]
• ${\displaystyle \sum _{1\leq k\leq n \atop (k,n)=1}\!\!k={\tfrac {1}{2}}n\varphi (n)}$, untuk ${\displaystyle n>1}$
• ${\displaystyle \sum _{k=1}^{n}\varphi (k)={\tfrac {1}{2}}\left(1+\sum _{k=1}^{n}\mu (k)\left\lfloor {\frac {n}{k}}\right\rfloor ^{2}\right)={\frac {3}{\pi ^{2}}}n^{2}+O\left(n(\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}$ (^[3] dikutip dalam^[4])

• ${\displaystyle \sum _{k=1}^{n}{\frac {\varphi (k)}{k}}=\sum _{k=1}^{n}{\frac {\mu (k)}{k}}\left\lfloor {\frac {n}{k}}\right\rfloor ={\frac {6}{\pi ^{2}}}n+O\left((\log n)^{\frac {2}{3}}(\log \log n)^{\frac {4}{3}}\right)}$ ^[3]
• ${\displaystyle \sum _{k=1}^{n}{\frac {k}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}n-{\frac {\log n}{2}}+O\left((\log n)^{\frac {2}{3}}\right)}$ ^[5]
• ${\displaystyle \sum _{k=1}^{n}{\frac {1}{\varphi (k)}}={\frac {315\,\zeta (3)}{2\pi ^{4}}}\left(\log n+\gamma -\sum _{p{\text{ prime}}}{\frac {\log p}{p^{2}-p+1}}\right)+O\left({\frac {(\log n)^{\frac {2}{3}}}{n}}\right)}$ ^[5]

(dengan ${\displaystyle \gamma }$ adalah konstanta Euler–Mascheroni).

• ${\displaystyle \sum _{\stackrel {1\leq k\leq n}{\operatorname {gcd} (k,m)=1}}\!\!\!\!1=n{\frac {\varphi (m)}{m}}+O\left(2^{\omega (m)}\right)}$

dimana ${\displaystyle m>1}$ adalah bilangan bulat positif dan ${\displaystyle \omega (m)}$ adalah jumlah faktor prima yang berbeda dari ${\displaystyle m}$.^[6]

Beberapa bilangan

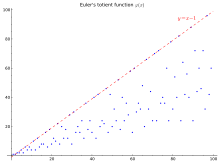
100 nilai pertama (barisan A000010 pada OEIS) ditampilkan pada tabel dan grafik di bawah ini:

${\displaystyle \varphi (n)}$ untuk ${\displaystyle 1\leq n\leq 100}$

+	1	2	3	4	5	6	7	8	9	10
0	1	1	2	2	4	2	6	4	6	4
10	10	4	12	6	8	8	16	6	18	8
20	12	10	22	8	20	12	18	12	28	8
30	30	16	20	16	24	12	36	18	24	16
40	40	12	42	20	24	22	46	16	42	20
50	32	24	52	18	40	24	36	28	58	16
60	60	30	36	32	48	20	66	32	44	24
70	70	24	72	36	40	36	60	24	78	32
80	54	40	82	24	64	42	56	40	88	24
90	72	44	60	46	72	32	96	42	60	40

Dalam grafik di kanan atas baris ${\displaystyle y=n-1}$ adalah batas atas valid untuk semua ${\displaystyle n}$ selain satu, dan dicapai jika dan hanya jika ${\displaystyle n}$ adalah bilangan prima. Batas bawah sederhana adalah ${\displaystyle \varphi (n)\geq {\sqrt {\frac {n}{2}}}}$, yang agak longgar: sebenarnya, lower limit dari grafik sebanding dengan ${\displaystyle {\frac {n}{\log \log n}}}$.^[7]

Fungsi pembangkit

Deret Dirichlet untuk ${\displaystyle \varphi (n)}$ dapat ditulis dalam istilah fungsi zeta Riemann sebagai:^[8]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)}{n^{s}}}={\frac {\zeta (s-1)}{\zeta (s)}}.}$

Fungsi pembangkit deret Lambert adalah^[9]

${\displaystyle \sum _{n=1}^{\infty }{\frac {\varphi (n)q^{n}}{1-q^{n}}}={\frac {q}{(1-q)^{2}}}}$

konvergen untuk ${\displaystyle |q|<1}$.

Keduanya dibuktikan dengan manipulasi deret dasar dan rumus untuk ${\displaystyle \varphi (n)}$.

Rasio bilangan berurutan

Pada tahun 1950 Somayajulu membuktikan^[10][11]

${\displaystyle \lim \inf {\frac {\varphi (n+1)}{\varphi (n)}}=0}$ dan ${\displaystyle \lim \sup {\frac {\varphi (n+1)}{\varphi (n)}}=\infty }$

Pada tahun 1954 Schinzel dan Sierpiński memperkuat ini, membuktikan^[10][11] bahwa himpunan

${\displaystyle \left\{{\frac {\varphi (n+1)}{\varphi (n)}},\;\;n=1,2,\ldots \right\}}$

adalah padat dalam bilangan riil positif. Mereka pun membuktikannya^[10] bahwa himpunan

${\displaystyle \left\{{\frac {\varphi (n)}{n}},\;\;n=1,2,\ldots \right\}}$

padat dalam interval ${\displaystyle (0,1)}$.

Lihat pula

• Fungsi Carmichael
• Konjektur Duffin–Schaeffer
• Generalisasi teorema kecil Fermat
• Bilangan komposit tinggi
• Grup perkalian bilangan bulat modulo n
• Jumlah Ramanujan
• Fungsi penjumlahan total

Catatan

Referensi

Pranala luar

• Hazewinkel, Michiel, ed. (2001) [1994], "Totient function", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4 
• Euler's Phi Function and the Chinese Remainder Theorem — proof that φ(n) is multiplicative Diarsipkan 2021-02-28 di Wayback Machine.
• Euler's totient function calculator in JavaScript — up to 20 digits Diarsipkan 2023-07-06 di Wayback Machine.
• Dineva, Rosica, The Euler Totient, the Möbius, and the Divisor Functions Diarsipkan 2021-01-16 di Wayback Machine.
• Plytage, Loomis, Polhill Summing Up The Euler Phi Function Diarsipkan 2023-05-23 di Wayback Machine.