Vektortér

A „Tér” lehetséges további jelentéseiről lásd: Tér (egyértelműsítő lap).

A vektortér, más néven lineáris tér a lineáris algebra egyik legalapvetőbb fogalma, amelyhez a geometriában (is) használt vektor fogalmának általánosítása vezet. A vektorokkal végezhető műveletek legelemibb tulajdonságait axiomatikusan definiálja, ezáltal egy algebrai struktúra-típus keletkezik. A lineáris tér a mi szokásos síkunk és terünk általánosítása többdimenziós terekre. Jelentősége nem csupán elméleti, a fizikában, informatikában, a komputergrafikában, számos más elméleti és alkalmazott tudományágban; nemkülönben a matematika számos területén fontos szerepet játszik.

Formális definíció

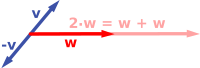
Legyen F egy test. Egy V nemüres halmazt vektortérnek nevezünk az F test felett, ha

• V halmazon értelmezve van egy összeadás nevű művelet, V × V → V függvény, ∀ u, v ∈ V elempárhoz hozzárendel egy és csak egy V-beli elemet (u+v), valamint
• F és V között értelmezve van egy skalárral való szorzás nevű művelet, F × V → V függvény, ∀ λ ∈ F és v ∈ V elempárhoz egyértelműen hozzárendel egy V-beli elemet (λv),

úgy, hogy az alábbi azonosságok, úgynevezett vektortér-axiómák teljesülnek:

1. V az összeadásra nézve kommutatív csoportot, Abel-csoportot alkot, azaz az összeadás:
   • asszociatív: ∀ u, v, w ∈ V: u + (v + w) = (u + v) + w.
   • kommutatív: ∀ u, v ∈ V: u + v = v + u.
   • létezik neutrális elem: 0 ∈ V, V nullvektora: v + 0 = v, ∀ v ∈ V.
   • invertálható: ∀ v ∈ V: ∃ olyan -v ∈ V additív inverz: v + (-v) = 0.
2. Skalárral való szorzás disztributivitási szabályai:
   • ∀ λ ∈ F és u, v ∈ V: λ(u + v) = λu + λv. (disztributivitási szabály)
   • ∀ λ, μ ∈ F és v ∈ V: (λ + μ)v = λv + μv.(disztributivitási szabály)
   • ∀ λ, μ ∈ F és v ∈ V: λ(μv) = (λμ)v. (asszociativitási szabály)
   • ∀ v ∈ V: 1v = v, ahol 1 az F test egységeleme.

Formálisan tehát úgy definiálhatjuk a vektortereket, figyelembe véve, hogy ${\displaystyle \mathbf {F} =\langle F,+,-,0,\cdot ,1\rangle }$ egy test,
az F feletti vektortér egy algebrai struktúra, a következő formában

${\displaystyle \mathbf {V} =\langle V,\oplus ,-\!\!-,\mathbf {0} ,F,+,-,0,\cdot ,1,\star \rangle }$

úgy, hogy

${\displaystyle \langle V,\oplus ,-\!\!-,\mathbf {0} \rangle }$ Abel-csoport,

${\displaystyle \star :F\times V\mapsto V}$ skalárral való szorzás, melyre teljesülnek a fent említett disztributivitási szabályok.

Ekkor a V vektortér struktúráját a következőképpen is jelölhetjük

${\displaystyle \langle V,\oplus ,-\!\!-,\mathbf {0} ,\mathbf {F} ,\star \rangle }$

V elemeit vektoroknak, F elemeit skalároknak nevezzük.
Megkülönböztetünk úgynevezett speciális vektortereket is, amelyeken még egyfajta szorzás is értelmezett.
Ilyenek például a skaláris szorzattal ellátott euklideszi terek.

Elemi tulajdonságok

V Abel-csoport

• nullvektor és az additív inverz unicitása,
• bármely u,v,w,t ∈ V: az u+x = v, és y+w = t egyenletek egyértelműen megoldhatók V-ben x és y-ra,
• összeadás asszociativitása és kommutativitása miatt többtagú összegek esetén a zárójelezés és a tagok sorrendje is tetszőlegesen megváltoztatható.

További következmények

• bármely λ ∈ F: λ0 = 0,
• bármely v ∈ V: 0v = 0, ahol 0 az F test nulleleme,
• bármely v ∈ V: (-1)v = -v, ahol -1 az F test egységelemének additív inverze,
• ha λv = 0, akkor λ = 0 vagy v = 0.
• (-λ)v = -(λv) = λ(-v)

Példák

A lineáris tér egy nagyon általános fogalom, rengeteg példa van rá a matematikában. Nagyon sok olyan matematikai fejezetben is megjelenik, amit szerteágazóan alkalmaznak a fizika számos területén, például a funkcionálanalízis vagy éppen a differenciálgeometria, hogy csak néhányat említsünk.

• a közönséges síkbeli és térbeli, origóból kiinduló vektorok a valós test felett a szokásos vektorösszeadásra és skalárral való szorzásra nézve,
• a valós szám n-esek ${\displaystyle \mathbb {R} }$ felett, a komplex szám n-esek ${\displaystyle \mathbb {C} }$ felett, és
• általában F ⁿ, F felett (F tetszőleges test), a szokásos módon értelmezett, komponensenként végzett műveletekre; ezeket a vektorokat általában oszlopvektorként ábrázolják,
• F ^{n × k}, F felett, azaz az n×k-as mátrixok F test felett, a mátrixok szokásos, komponensenkénti összeadására és skalárral való szorzására nézve.
• F [x], azaz az F feletti polinomok, F felett, a polinomok összeadására és skalárral való szorzására nézve,
• a legfeljebb n-edfokú polinomok F felett,
• valós számsorozatok a valós test felett a szokásos műveletekre,
• az ${\displaystyle \left[a,b\right]}$ intervallumon folytonos ${\displaystyle \mathbb {R} }$-be képező függvények a valós test felett, a szokásos pontonkénti összeadásra, és skalárral való szorzásra nézve,
• az ${\displaystyle \left[a,b\right]}$ intervallumon Riemann-integrálható ${\displaystyle \mathbb {R} }$-be képező függvények a valós számok teste felett, a szokásos pontonkénti összeadásra, valamint a skalárral való szorzásra nézve,
• a komplex számok a valós test felett, a komplex számok körében értelmezett műveletekre,
• a komplex számok a komplex számok teste felett,
• a valós számok a valós számok teste felett,
• a komplex számok a valós számok felett,
• a valós számok a racionális számok felett,
• általában, testbővítés esetén a bővebb test a szűkebb felett,
• a valószínűségi változók a szokásos összeadásra és skalárral való szorzásra nézve,
• az euklideszi sík, illetve tér eltolásai, hiszen az eltolások egymás utáni végzése megfelel a vektorok összeadásának, és a skalárszoros eltolás megfelel az eltolásvektor skalárszorosának. A nullelem az identitás, aminek megfelelője a nullvektor.

Lineáris altér

Bővebben: Lineáris altér

Egy F test feletti V vektortér egy nemüres W ⊆ V részhalmazát altérnek nevezzük V-ben, ha W maga is vektortér ugyanazon F test felett ugyanazokra a V-beli vektorműveletekre, precízebben ezeknek a műveleteknek W-re történő megszorításaira nézve. Jelölése W ≤ V. Mivel W vektortér, azért tartalmazza a nullvektort.

Minden vektortér tartalmazza önmagát és a csak nullvektorból álló vektorteret. Minden altér előáll a másik vektortér képeként úgy, hogy egy lineáris leképezés leképez egy másik vektorteret a tartalmazó vektortérbe; és magtérként is úgy, hogy egy lineáris leképezés leképezi a tartalmazó vektorteret egy másik vektortérbe. Ekvivalenciaosztályok képzésével egy vektortérből és alteréből hányadostér, más néven vektortér állítható elő; ami összefügg az altérnek azzal a tulajdonságával, hogy előáll képként, lásd homomorfizmustétel.

Lineáris leképezések

A lineáris leképezések egy vektorteret egy másikba képeznek a struktúra megtartásával. Az univerzális algebra szerint homomorfizmusok a vektorterek között. Egy ugyanazon ${\displaystyle K}$ test fölött definiált ${\displaystyle U}$ vektorteret ${\displaystyle V}$ vektortérbe vivő ${\displaystyle f\colon U\to V}$ függvény lineáris leképezés, ha minden ${\displaystyle a,b\in U}$ és minden ${\displaystyle \lambda \in K}$ esetén:

• ${\displaystyle f(a+b)=f(a)+f(b)}$
• ${\displaystyle f(\lambda a)=\lambda f(a)}$

Ekkor ${\displaystyle f}$ kompatibilis a struktúrákkal, amelyek a vektorteret felépítik: az összeadással és a skalárral szorzással. Két vektortér izomorf, ha van köztük bijektív lineáris leképezés, vagyis van inverz függvény. Ez az inverz függvény automatikusan lineáris. Az izomorf vektorterek nem különböznek egymástól struktúrájukban.

Lineáris kombináció

Bővebben: Lineáris kombináció

V vektortér v₁, v₂, …, v_k tetszőleges vektorai és λ₁, λ₂, …, λ_k ∈ F skalárok.
Ekkor a ${\displaystyle \lambda _{1}\mathbf {v} _{1}+\ldots +\lambda _{k}\mathbf {v} _{k}}$ ∈ V vektort a v_i vektorok, λ_i skalárokkal képzett lineáris kombinációjának nevezzük.

Lineáris függetlenség

Bővebben: Lineáris függetlenség

Egy V vektortér véges sok vektoráról akkor mondjuk, hogy lineárisan függetlenek, ha lineáris kombinációjuk csak úgy lehet a nullvektor, ha mindegyik skalár szükségképpen 0. Végtelen sok vektor lineáris függetlenségén azt értjük, hogy közülük bármely véges sok lineárisan független. A v₁,…,v_n ∈ V vektorok lineárisan összefüggőek, ha lineárisan nem függetlenek, tehát

${\displaystyle \exists \ \lambda _{1},\ldots ,\lambda _{n}\in \mathbf {F} }$

nem mind nulla skalár, azaz közülük legalább egy nem nulla, hogy

${\displaystyle \lambda _{1}\mathbf {v} _{1}+\ldots +\lambda _{n}\mathbf {v} _{n}=\mathbf {0} .}$

Lineáris burok

Néhány vektor lineáris burka az a vektorhalmaz, ami előáll a vektorok lineáris kombinációjaként. Ez egy altér, és a legkisebb vektortér, ami a vektorokat tartalmazza.

Bázis

Bővebben: Vektortér bázisa

A bázis a lineáris algebrában egy olyan vektorhalmazt jelent, mely vektorainak lineáris kombinációi reprezentálják egy megadott vektortér valamennyi vektorát, valamint e vektorhalmaz semelyik eleme sem fejezhető ki a többi elem lineáris kombinációjával.
Tehát bázison lineárisan független generátorrendszert értünk.

Feltéve a kiválasztási axiómát, a Zorn-lemma biztosítja, hogy minden vektortérnek van bázisa. A Zermelo-Frankel axiómarendszerben ez az állítás ekvivalens a kiválasztási axiómával.

Ha egy vektort kifejezzük egy generátorrendszer elemeinek lineáris kombinációjaként, akkor a lineáris kombinációban szereplő skalárok a vektor koordinátái az adott bázisban. Egy generátorrendszerben a vektortér minden vektora kifejezhető koordinátákkal; azonban, ha a generátorrendszer nem lineárisan független, akkor ez nem egyértelmű; viszont egy bázisban a koordináták már egyértelműek. Ez megkönnyíti a számításokat, mivel a vektorok helyett koordinátavektorok használhatók.

Dimenzió

Bővebben: Dimenzió (lineáris algebra)

Ha adott egy V vektortér, akkor minden bázisának elemszáma, számossága ugyanaz. Ez a számosság a V vektortér dimenziója. Ha a vektortérnek nincs véges generátorrendszere, akkor dimenziója végtelen. A 0 tér dimenziója: 0.

Két, azonos test fölötti vektortér akkor és csak akkor izomorf, ha dimenziójuk megegyezik. Ez lehetővé teszi, hogy a vektorterek bázisainak elemei megfeleljenek egymásnak, ami kiterjeszthető lineáris leképezéssé; így a véges vektorterek közötti lineáris leképezések mátrixszal ábrázolhatók.

Vektorterek izomorfizmusa

Definíció

Két vektortér, V₁ és V₂ izomorf egymással, ha létezik egy kölcsönösen egyértelmű, injektív lineáris (homogén) leképezés V₁-ből V₂-re.

Azaz

${\displaystyle V_{1}\cong V_{2}\ \Leftrightarrow \ \varphi :V_{1}\rightarrow V_{2}\ }$ lineáris leképezés bijektív.

A vektorterek halmazán az izomorfia meghatároz egy osztályozást. Ez az osztályozás a halmazt diszjunkt részhalmazok uniójára bontja fel. Két vektortér akkor és csak akkor kerül ugyanabba az osztályba, ha izomorf.
E reláció reflexív, szimmetrikus és tranzitív, vagyis az izomorfia ekvivalenciareláció.

Magtér, képtér

Ha ${\displaystyle \varphi :V\rightarrow W}$ tetszőleges lineáris leképezés, akkor a magtér és a képtér

${\displaystyle \mathrm {Ker} \,\varphi =\{\,\mathbf {v} \in V\,|\,\varphi (\mathbf {v} )=0\,\}}$

${\displaystyle \mathrm {Im} \,\varphi =\{\mathbf {w} \in W\,|\,\exists \ \mathbf {v} \in V:\ \varphi (\mathbf {v} )=\mathbf {w} \}}$

Megjegyzés: a magtér a V, a képtér a W vektortér altere.

Tulajdonságok

Véges dimenziós vektorterek tulajdonságai

• Egy ${\displaystyle \varphi :V\rightarrow W}$ lineáris leképezés akkor és csak akkor izomorfizmus, ha

${\displaystyle \mathrm {Ker} \,\varphi =\mathbf {0} \ \wedge \ \mathrm {Im} \,\varphi =W}$

• Ha V vektortér F felett, valamint

${\displaystyle \mathrm {dim} \,V=n,\ n\in \mathbb {N} ^{+}\Rightarrow V\cong \mathbf {F} ^{n}}$

• Ugyanazon F test feletti véges dimenziós vektorterekre fennáll:

${\displaystyle V\cong W\Leftrightarrow \mathrm {dim} \,V=\mathrm {dim} \,W}$

Dimenziótétel

Bővebben: Dimenziótétel

A dimenziótétel azt állítja, hogy tetszőleges lineáris leképezés képterében illetve magterében lévő bármely lineáris független generátorrendszer összelemszáma a kiindulási vektortér dimenziójával egyenlő. Formálisan

V₁ és V₂, két tetszőleges, véges dimenziós vektortér ugyanazon F test felett, továbbá ${\displaystyle \varphi \ }$ tetszőleges lineáris leképezés V₁-ből V₂-be. Ekkor

${\displaystyle \mathrm {dim\,Ker} \,\varphi +\mathrm {dim\,Im} \,\varphi =\mathrm {dim} \,V_{1}}$

Műveletek vektorterekkel

Homomorfizmus

Bővebben: Homomorfizmus

Az algebrában egy struktúra egy másikra vett leképezése homomorfizmus, ha megtartja az adott struktúrán végezhető műveleteket. Például vektortér esetén ez azt jelenti, hogy a leképezés megőrzi az összeadást és a skalárral szorzást. Legyenek ${\displaystyle U}$, ${\displaystyle V}$ vektorterek az ${\displaystyle F}$ test fölött; ekkor ${\displaystyle f\colon U\to V}$ homomorfizmus, ha minden ${\displaystyle a,b\in U}$ és minden ${\displaystyle \lambda \in F}$ esetén:

• ${\displaystyle f(a+b)=f(a)+f(b)}$
• ${\displaystyle f(\lambda a)=\lambda f(a)}$

ami éppen a lineáris leképezés definíciója.

Faktortér

V egy tetszőleges vektortér F felett, és U egy tetszőleges altere V-nek. A

${\displaystyle [\mathbf {v} ]=\mathbf {v} +U=\{\mathbf {v} +\mathbf {u} \,|\,\mathbf {u} \in \,U\}}$

halmazok, ahol v befutja az egész vektorteret, diszjunkt részhalmazok uniójára bontják V-t, ugyanis ha
${\displaystyle \mathbf {v} _{1}-\mathbf {v} _{2}\notin U}$ akkor ${\displaystyle [\mathbf {v} _{1}]}$ és ${\displaystyle [\mathbf {v} _{2}]}$ diszjunkt, ha ${\displaystyle \mathbf {v} _{1}-\mathbf {v} _{2}\in U}$ akkor ${\displaystyle [\mathbf {v} _{1}]=[\mathbf {v} _{2}].}$
Definiálunk két műveletet e halmazok körében

${\displaystyle [\mathbf {v} _{1}]+[\mathbf {v} _{2}]=[\mathbf {v} _{1}+\mathbf {v} _{2}]}$

${\displaystyle \alpha [\mathbf {v} _{1}]=[\alpha \mathbf {v} _{1}],\ \alpha \in \mathbf {F} }$

Az ily módon definiált műveletek egyértelműek, mivel

${\displaystyle [\mathbf {v} ]=[\mathbf {v} ']\ \Leftrightarrow \ \mathbf {v} -\mathbf {v} '=(\mathbf {v} +\mathbf {w} )-(\mathbf {v} '+\mathbf {w} )\in U\ \Leftrightarrow \ [\mathbf {v} +\mathbf {w} ]=[\mathbf {v} '+\mathbf {w} ],}$

${\displaystyle \alpha [\mathbf {v} ]=\alpha [\mathbf {v} ']\ \Leftrightarrow \ \alpha (\mathbf {v} -\mathbf {v} ')=\alpha \mathbf {v} -\alpha \mathbf {v} '\in U\ \Leftrightarrow \ [\alpha \mathbf {v} ]=[\alpha \mathbf {v} ']}$

Így egy vektorteret kaptunk, melyet a V vektortér U altere szerinti faktorterének nevezünk, vagy röviden a ${\displaystyle V/U\ }$ faktortér, szokás ${\displaystyle V\ }$ hányadosterének is nevezni.
A faktortér elemei a ${\displaystyle \ [\mathbf {v} ],\,\mathbf {v} \in V}$ vektorhalmazok, az additív egységelem a ${\displaystyle \ [\mathbf {0} ]=U.}$

Direkt összeg

Ha ${\displaystyle V,W}$ vektorterek ugyanazon test fölött, akkor direkt összegük az a vektortér, melynek elemei úgy képződnek, hogy az első komponens az első, a második komponens a második vektortér eleme:

${\displaystyle V\oplus W:=\left\{\left(v,w\right)\mid v\in V,w\in W\right\}}$

A vektorokat komponensenként adjuk össze és a skalárral szorzást is komponensenként végezzük. A ${\displaystyle V\oplus W}$ vektortér dimenziója a tagok dimenziójának összege. Az összeg elemeit ${\displaystyle (v,w)}$ helyett írják úgy is, mint ${\displaystyle v+w}$. A direkt összeg általánosítható véges és végtelen tagra is; utóbbi esetén csak véges sok tag különbözhet a nullvektortértől.

Direkt szorzat

Ha ${\displaystyle V,W}$ vektorterek ugyanazon test fölött, akkor direkt szorzatuk az a vektortér, melynek elemei úgy képződnek, hogy az első komponens az első, a második komponens a második vektortér eleme:

${\displaystyle V\times W=\left\{\left(v,w\right)\mid v\in V,w\in W\right\}}$.

A vektorokat komponensenként adjuk össze és a skalárral szorzást is komponensenként végezzük. A ${\displaystyle V\times W}$ vektortér dimenziója a tagok dimenziójának összege. A direkt összeg általánosítható véges és végtelen tényezőre is; utóbbi esetben akár végtelen sok tényező is különbözhet a nullvektortértől.

Tenzorszorzás

Ha ${\displaystyle V,W}$ vektorterek ugyanazon test fölött, akkor tenzorszorzatukat

${\displaystyle V\otimes W}$

jelöli. A tenzorszorzat elemeinek bilineáris ábrázolása:

${\displaystyle \sum _{i\in I}\sum _{j\in J}a_{ij}(v_{i}\otimes w_{j})}$,

ahol az ${\displaystyle a_{ij}}$ elemek skalárok, ${\displaystyle (v_{i})_{i\in I}}$ bázis ${\displaystyle V}$-ben és ${\displaystyle (w_{j})_{j\in J}}$ bázis ${\displaystyle W}$-ben. Ha ${\displaystyle V}$ vagy ${\displaystyle W}$ végtelen dimenziós, akkor csak véges sok tag különbözhet nullától. Ekkor ${\displaystyle V\otimes W}$ dimenziója ${\displaystyle V}$ és ${\displaystyle W}$ dimenziójának szorzata. A tenzorszorzás is általánosítható több vektortérre.

Vektorterek további struktúrával

A matematika több alkalmazásában, például a geometriában és az analízisben van, hogy nem elegendő a vektortér struktúra, hanem még további struktúrát is feltételezni kell; így biztosítva például normát vagy határérték létezését. Például:

• euklidészi vektorterek: skalárszorzattal ellátott valós vektortér. A prehilbertterek speciális esete.
• normált tér: egy olyan vektortér, amiben a vektoroknak hossza (normája) van. Ez egy nemnegatív szám, amire teljesül a háromszög-egyenlőtlenség.
• prehilberttér: skalárszorzattal ellátott valós vagy komplex vektortér. Egy ilyen térben a vektorok hossza mellett még a vektorok szöge is definiálható. A topologikus vektortér speciális esete.
• topologikus vektortér: topologikus tér fölötti vektortér, ahol a vektorok összeadása és a skalárral szorzás folytonos műveletek.
• unitér vektortér: többnyire komplex vektortér skalárszorzattal ellátva. A prehilberttér speciális esete.

Topologikus vektorterekben kezelhető a konvergencia, a teljesség és az egyenletes konvergencia. A teljes normált terek Banach-terek, a teljes prehilbertterek Hilbert-terek.

Általánosítások

• Ha a teret test helyett gyűrű felett definiáljuk, akkor modulust kapunk. Egyes szerzők csak kommutatív gyűrűk fölött definiálnak modulusokat. A kommutatív gyűrűk fölötti modulusok az Abel-csoport és a vektortér közös általánosításai.
• Egyes szerzők a ferdetestek fölötti modulusokat is vektortérnek nevezik. Kommutativitás hiányában beszélhetünk bal- és jobbvektorterekről. Ez a helyzet összehasonlítható nem kommutatív gyűrűk fölötti modulusokkal. A cikkben megadott definíció ekkor a balvektorterekhez vezet, mivel a skalár a bal oldalon áll. A jobbvektorterek ennek tükörképi párjai, a skalár jobb oldalon jelenik meg. Több alapvető eredmény átvihető ferdetestek fölé, például bázis létezése.
• Ha test helyett féltestet veszünk, akkor félvektorteret kapunk.
• Egy másik általánosítás a vektornyaláb, ami vektorterek egy topologikus tér pontjaival paraméterezett családja.

Történeti megjegyzés

Bartel Leendert van der Waerden megjegyzi, hogy tudomása szerint az n-dimenziós vektortér fogalmát először Hermann Günther Graßmann használta 1844-ben megjelent Die lineale Ausdehnungslehre című könyvében. Implicit már korábban is használták a fogalmat.

Kapcsolódó szócikkek

• Algebra
• Duális tér
• Lineáris algebra
• Lineáris leképezés
• Tenzor
• Tenzorszámítás
• Vektor

Irodalom

• Bronstejn – Szemengyajev – Musiol: Matematikai kézikönyv' (TypoTeX, 2002)
• Dancs I. – Puskás Cs.: Vektorterek (Aula Kiadó, 2003)
• Sain Márton: Matematikatörténeti ABC (Tankönyvkiadó, 1978)
• Scharnitzky Viktor: Mátrixszámítás. Bolyai-könyvek sorozat (Műszaki Könyvkiadó, 1998)
• Surányi László: Algebra, testek, gyűrűk, polinomok (TypoTeX, 2004)
• Szász Gábor: Matematika II. (Nemzeti Tankönyvkiadó, 2000)
• Szendrei János: Algebra és számelmélet (Nemzeti Tankönyvkiadó, 1996)

Források

• Freud Róbert: Lineáris algebra (ELTE Eötvös Kiadó, 2004)
• Fried Ervin: Algebra I., Elemi és lineáris algebra (Nemzeti Tankönyvkiadó, 2000)
• Kuros, A. G.: Felsőbb algebra (Tankönyvkiadó, Bp., 1975)
• Praszolov, V. V.: Lineáris algebra (TypoTeX, 2005)
• Gerd Fischer: Lineare Algebra. Vieweg-Verlag, ISBN 3-528-03217-0.
• R. Hartwig: Syntax, Semantik, Spezifikation - Grundlagen der Informatik. WS 2009/2010.

Fordítás

Ez a szócikk részben vagy egészben a Vektorraum című német Wikipédia-szócikk fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

További információk

• Encyclopedia Of Maths: Linear operator (angolul)
• MathWorld: Linear algebra (angolul)
• MathWorld: Linear transformation (angolul)
• PlanetMath: Linear algebra Archiválva 2012. június 12-i dátummal a Wayback Machine-ben (angolul)
• PlanetMath: Linear transformation Archiválva 2007. szeptember 30-i dátummal a Wayback Machine-ben (angolul)
• Wikipedia: Algebra (angolul)
• Wikipedia: Euclidean space (angolul)
• Wikipedia: Linear Map (angolul)
• Wikipedia: Linear algebra (angolul)
• Wikipedia: Normed vector space (angolul)
• Wikipedia: Topological vector space (angolul)