Szorzás

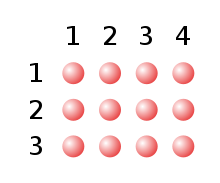
Szorzás vagy sokszorozás, a számtani alapműveletek egyike. Ha a és b pozitív egész számokat jelentenek, akkor b-t megszorozni a-val annyit tesz, mint alkotni a

${\displaystyle \sum _{i=1}^{a}b=\underbrace {b+b+\dots +b} _{a}}$

összeget, amelyet röviden ab-vel szokás megjelölni. A b számot, amelyet ezen összeg előállítása végett a-szor tettünk összeadandónak, sokszorozandónak vagy szorzandónak, az a számot sokszorozónak vagy szorzónak, az eredményül nyert összeget pedig szorzatnak nevezzük.

Bebizonyítható, hogy

• ab = ba, azaz a szorzás kommutatív.
• (ab)c = a(bc), azaz a szorzás asszociatív.
• a(b + c) = ab + ac, azaz a szorzás disztributív az összeadásra és a kivonásra nézve.

Minthogy a szorzandó felcserélhető a szorzóval anélkül, hogy a szorzat értéke ennek következtében megváltoznék, még az elnevezésben sem szükséges azokat egymástól megkülönböztetni, és ezért mind a kettőt a szorzat tényezőinek nevezzük. Több pozitív egész szám szorzatát úgy alkotjuk, hogy az elsőt megszorozzuk a másodikkal, a nyert szorzatot a harmadikkal stb:

${\displaystyle \prod _{i=1}^{n}a_{i}=a_{1}\cdot a_{2}\cdot \dots a_{n}=(\dots (((a_{1}\cdot a_{2})\cdot a_{3})\cdot a_{4})\dots )\cdot a_{n}}$

A kommutativitás miatt az ilyen szorzat értéke is független a megadott tényezők sorrendjétől.

A szorzás megfordítása az osztás.

Ha a pozitív egész számok halmazán kívül első tagokkal akarjuk elvégezni a szorzást, akkor e művelet értelmezését módosítanunk kell. Különféle számhalmazokon úgy szokás definiálni, hogy a szorzás jelentése ne változzon, ha az újabb számhalmazt a régebbi kibővítésének tekintjük. A szorzás természetes, egész, racionális, valós és komplex számok halmazán is kommutatív, asszociatív és disztributív művelet.

Általánosítás

A szorzás kétváltozós műveletként általánosítható más algebrai struktúrákra, például mátrix- és függvényhalmazokra is. A mátrixszorzás asszociatív és disztributív, de nem kommutatív.

Jelölések

A szorzást számok esetén szorzóponttal vagy szorzókereszttel jelölik:

${\displaystyle 2\cdot 3=6}$ (Kétszer három az hat)

${\displaystyle 3\cdot 4=12}$

${\displaystyle 2\cdot 3\cdot 5=6\cdot 5=30}$

${\displaystyle 2\cdot 2\cdot 2\cdot 2\cdot 2=32}$

vagy

${\displaystyle 2\times 3=6}$

${\displaystyle 3\times 4=12}$

${\displaystyle 2\times 3\times 5=6\times 5=30}$

${\displaystyle 2\times 2\times 2\times 2\times 2=32}$

• Egymás után írás; ez az algebrában szokásos, és mindenütt, ahol betűjelölések szerepelnek. Például xy vagy 5x.
• Vektorok esetén kétféle szorzást is értelmeznek: a skaláris és a vektoriális szorzást. A skaláris szorzatot szorzópont, a vektoriális szorzatot szorzókereszt jelöli.
• Programnyelvekben a * csillag a szorzójel. Ezt azért választották így, mert minden billentyűzeten rajta van, és jobban látszik a régi képernyőkön. Ez a FORTRAN programozási nyelvből ered.

Algoritmusok

Az írásbeli szorzás szokásos módja a szorzótábla ismeretét igényli, de van olyan módszer is, ami anélkül is működik.

A nagy számok kézzel való szorzása időigényes és sok hibalehetőséget hordoz magában. Ennek megkönnyítésére használják a tízes alapú logaritmust. Logarléccel három számjegyes pontossággal lehet szorozni. A huszadik század elején a mechanikus számológépek, mint például a Marchant 10 számjegyes pontosságot is lehetővé tettek. A modern elektromos számológépek és a számítógépek nagyban csökkentették a kézi számítások iránti igényt.

Történelmi algoritmusok

Különböző módszerek maradtak fenn az ókori Egyiptomból, Babilonból, Görögországból, az Indus-völgyből és Kínából.

Egyiptom

Az egyiptomi módszer a Jahmesz által írt Rhind-papirusz szerint sorozatos kétszerezésen, felezésen és összeadáson alapul. Például a 13 és a 21 összeszorzásához háromszor kétszerezték meg a 21-et:

${\displaystyle 1\cdot 21=21}$, ${\displaystyle 2\cdot 21=42}$, ${\displaystyle 4\cdot 21=84}$, ${\displaystyle 8\cdot 21=168}$.

A 13-at háromszor elfelezték:

${\displaystyle 13:2=6}$, marad ${\displaystyle 1}$; ${\displaystyle 6:2=3}$, nem marad semmi; ${\displaystyle 3:2=1}$, marad az ${\displaystyle 1}$.

A szorzatot a megfelelő kétszerezések összegeként állították elő:

${\displaystyle 13\cdot 21=(1+4+8)\cdot 21=(1\cdot 21)+(4\cdot 21)+(8\cdot 21)=21+84+168=273}$.

Babilon

Babilonban a hatvanas számrendszert használták, hasonlóan a mai tízes számrendszerhez. A szorzás a mai tízes számrendszerbeli szorzáshoz hasonlóan működött. Mivel nehéz emlékezni a ${\displaystyle 60\cdot 60}$ szorzatra, ezért a babiloni matematikusok szorzótáblázatokat használtak. Ezek a táblák tartalmazták egy szám első húsz szorzatát, amit a szám tízszereseinek szorzatai követtek. Egy szorzás végrehajtásához, például az ${\displaystyle 53n}$ kiszámításához külön kellett összeszorozni 50-nel és 3-mal, majd ezeket a szorzatokat összeadni.

Kína

A Zhou Pei Suan Ching (Kr.e. 300-nál korábbról) és Kilenc fejezet a matematika művészetéről matematikai könyvekben a számítások szavakkal vannak leírva. Ismert viszont, hogy az ókori kínai matematikusok abakuszt használtak a számítások elvégzéséhez.

Indus-völgy

Az Indus-völgye korai hindu matematikusai számos intuitív módszert alkalmaztak a szorzásra. A számolásokat általában kis palatáblákon végezték.

Modern módszer

A modern módszer az arab számíráson és a tízes számrendszeren alapul. Brahmagupta módszert adott az összeadás, kivonás, szorzás, osztás műveletére; ő írta le elsőként a modern módszert.

Henry Burchard Fine, a Princeton matematikaprofesszora szerint az indiaiak nemcsak a helyi értékes tízes számrendszert fedezték fel, hanem az ahhoz tartozó alapvető eljárásokat is.^[1]

Szorzássorozat

Jelölés

A szorzássorozat jele a görög nagy pí Π betűből származik. Az Unicode-ban is megkülönböztetik ezt a két jelet: U+220F (∏) jelöli a szorzássorozat jelét, és U+03A0 (Π) a betűt. Ez a jelölés a következőt jelenti:

${\displaystyle \prod _{i=m}^{n}x_{i}=x_{m}\cdot x_{m+1}\cdot x_{m+2}\cdot \,\,\cdots \,\,\cdot x_{n-1}\cdot x_{n}.}$

ahol az alsó index mutatja a futó változót, és annak alsó határát, míg a felső index a felső határt jelöli. A futó index az alsó határtól egyesével megy el egészen a felső határig. A szorzássorozat jele után következnek a tényezők, amik a futó index egymást követő értékeit behelyettesítve kaphatók.

Például

${\displaystyle \prod _{i=2}^{6}\left(1+{1 \over i}\right)=\left(1+{1 \over 2}\right)\cdot \left(1+{1 \over 3}\right)\cdot \left(1+{1 \over 4}\right)\cdot \left(1+{1 \over 5}\right)\cdot \left(1+{1 \over 6}\right)={7 \over 2}.}$

Olvasd: Produktum i=2-től 6-ig, zárójelben az 1+1/i egyenlő...

Ha az alsó határ egyenlő a felső határral, akkor a szorzat egy tényezős, és értéke ez a tényező. Ha az alsó határ nagyobb, mint a felső, akkor a szorzat üres, és értéke definíció szerint 1.

Végtelen szorzat

Végtelen sok tényező is összeszorozható, így végtelen szorzat keletkezik. A jelölésben a felső határt ${\displaystyle \infty }$, az alsó határt ${\displaystyle -\infty }$ jelölheti. A végtelen szorzat értéke

${\displaystyle \prod _{i=m}^{\infty }x_{i}=\lim _{n\to \infty }\prod _{i=m}^{n}x_{i}.}$

feltéve, hogy a határérték létezik.

A mindkét irányban végtelen szorzat értéke

${\displaystyle \prod _{i=-\infty }^{\infty }x_{i}=\left(\lim _{m\to -\infty }\prod _{i=m}^{0}x_{i}\right)\cdot \left(\lim _{n\to \infty }\prod _{i=1}^{n}x_{i}\right),}$

feltéve, hogy a határértékek léteznek.

Értelmezés

Descartes-szorzat

A szorzás ismételt összeadásként való értelmezése egyenes utat biztosít a szorzás halmazelméleti értelmezéséhez a számosságok körében.

A ${\displaystyle \displaystyle n\cdot a=\underbrace {a+\cdots +a} _{n},}$ kifejezésben a n másolatát adjuk össze. Ennek egyik módja az indexelés, ahol ${\displaystyle a_{1},a_{2},\ldots ,a_{n}}$, így a diszjunkt példányait uniózzuk össze. Ez éppen az ${\displaystyle n\times a\,}$ Descartes-szorzat. A természetes számok szorzásának tulajdonságai azonnal adódnak a Descartes-szorzás megfelelő tulajdonságaiból.

Peano-axiómák

Giuseppe Peano javasolta a Peano-axiómákon alapuló következő definíciót:^[2]

${\displaystyle a\times 1=a}$

${\displaystyle a\times b'=(a\times b)+a}$

ahol b′ jelöli b rákövetkezőjét. A többi Peano-axióma segítségével bizonyíthatók a szorzás ismert tulajdonságai.

Halmazelmélet

A halmazelmélet segítségével is lehetséges rekurzív definíciót adni a szorzásra, bár ez bonyolult. Ez a definíció visszanyúlik a Peano-féle definíciókhoz.

Geometria

A párhuzamos szelők tétele lehetőséget ad rá, hogy két adott hosszúságú szakasz hosszának szorzatával megegyező hosszúságú szakaszt szerkesszünk.

Különböző számkörök

A szám jelenthet mennyiséget (3 alma), sorszámot (a harmadik alma), vagy mértéket (3,5 méteres magasság). Ahogy a történelemben a matematika az ujjakon való számlálástól a kvantummechanikáig, úgy terjeszkedett a szorzás az egyre elvontabb számkörök és más matematikai objektumok (polinomok, mátrixok) felé.

Egész számok

Az egész számok szorzásának szabálya a természetes számok szorzásának szabályaiból és az előjelszabályból következik:

Ha az M és az N egész mindegyike pozitív, akkor ${\displaystyle M\times N}$ egy olyan tömbben levő elemek számát jelöli, ahol minden oszlopban M, és minden sorban N elem van.

Az előjelszabály szerint

${\displaystyle (-N)\times M=N\times (-M)=-(N\times M)}$

és

${\displaystyle (-N)\times (-M)=N\times M}$

Ugyanez az előjelszabály érvényes a racionális és a valós számok szorzására.

Racionális számok

A törtek szorzásának szabálya: számlálót számlálóval, és nevezőt nevezővel szorzunk:

${\displaystyle {\frac {A}{B}}\times {\frac {C}{D}}={\frac {(A\times C)}{(B\times D)}}}$.

Ez a szorzat megadja annak a téglalapnak a területét, ami ${\displaystyle {\frac {A}{B}}}$ hosszú és ${\displaystyle {\frac {C}{D}}}$ széles.

Valós számok

Két valós szám szorzatát határértékként adhatjuk meg: (x·y) az a valós szám, ami megkapható egy x-hez és egy y-hoz konvergáló sorozat megfelelő elemeinek összeszorzásával keletkezett újabb sorozat határértékeként. Képletekkel felírva ugyanez: ha ${\displaystyle (x_{n})}$ és ${\displaystyle (y_{n})}$ két sorozat, és

${\displaystyle \lim _{n\rightarrow \infty }x_{n}=x}$

és

${\displaystyle \lim _{n\rightarrow \infty }y_{n}=y,}$

akkor

${\displaystyle x\cdot y{\overset {def}{=}}\lim _{n\rightarrow \infty }(x_{n}\cdot y_{n}).}$

Pozitív valós számok esetében a szorzat megadja annak a téglalapnak a területét, ami x hosszú és y széles.

Komplex számok

A ${\displaystyle z_{1}}$ és a ${\displaystyle z_{2}}$ komplex számot az ${\displaystyle (a_{1},b_{1})}$ és az ${\displaystyle (a_{2},b_{2})}$ valós számpárokként tekintve ${\displaystyle z_{1}}$ és ${\displaystyle z_{2}}$ szorzata a következőképpen adódó komplex szám:

${\displaystyle z_{1}\cdot z_{2}=(a_{1}\cdot a_{2}-b_{1}\cdot b_{2},a_{1}\cdot b_{2}+a_{2}\cdot b_{1}),}$

mert ha az i imaginárius egységgel írjuk fel

${\displaystyle z_{1}=a_{1}+b_{1}\cdot i,}$

${\displaystyle z_{2}=a_{2}+b_{2}\cdot i,}$

${\displaystyle z_{1}\cdot z_{2}=(a_{1}+b_{1}\cdot i)\cdot (a_{2}+b_{2}\cdot i)=a_{1}\cdot a_{2}+a_{1}\cdot b_{2}\cdot i+a_{2}\cdot b_{1}\cdot i+b_{1}\cdot b_{2}\cdot i^{2}=}$

${\displaystyle =a_{1}\cdot a_{2}-b_{1}\cdot b_{2}+(a_{1}\cdot b_{2}+a_{2}\cdot b_{1})\cdot i,}$

ahol kihasználtuk, hogy

${\displaystyle i^{2}=-1.}$

Ez a szorzatkifejezés valós számokra egyszerűen ${\displaystyle a_{1}\cdot a_{2}}$-vel azonos, mivel valós számok esetében a b₁ és b₂ képzetes részek nullák.

Polinomok és mátrixok

A szorzás a számokon kívül polinomokra és mátrixokra is kiterjeszthető. A polinomok és adott n-re az n×n-es mátrixok gyűrűt alkotnak, ahol lehet összeadni, kivonni és szorozni. A polinomszorzás kommutatív, de a mátrixszorzás nem.

Absztrakt algebra

Csoportok

Sok halmaz a szorzással megfelel a csoport definíciójának. Ezek az asszociativitás, az egységelem és az inverzek megléte, és a halmaz zártsága a műveletekre.

Egy egyszerű példa a nem nulla valós számok halmaza. Az egységelem az 1. A nullát azért kell kizárni, mert nincs inverze: nincs olyan szám, amivel megszorozva a nullát 1-et kapunk. Ez a példa egy kommutatív, azaz Abel-csoport.

Nem minden csoport kommutatív. Nézzük például az adott méretű invertálható mátrixok csoportját egy adott test felett. Az egységelem az identitásmátrix, az inverzek a mátrixinverzek, és a szorzásra való zártság is teljesül. Mivel a mátrixszorzás nem kommutatív, ezért ez a csoport nem kommutatív.

Az egész számok halmaza nem csoport a szorzásra, még a nulla nélkül sem, mert az 1-en és a -1-en kívül nincsenek inverzek.

A csoportelméletben a szorzást ponttal, vagy egymás mellé írással jelölik. Így az a és a b elemek szorzata ab vagy ${\displaystyle \mathbf {a} \cdot \mathbf {b} .}$

Gyűrűk

A gyűrű egy másik algebrai struktúra, amiben szorozni lehet. Lehet még összeadni és kivonni is. A gyűrűkben nincs minden elemnek (multiplikatív) inverze: például a nullelemnek nincs, és ha a gyűrűben vannak nullosztók, akkor azoknak sincs. A legegyszerűbb példák gyűrűkre az egész számok, a polinomgyűrűk és a mátrixgyűrűk.

A kommutatív, egységelemes, nullosztómentes gyűrűk az integritási tartományok. Erre a legegyszerűbb példa az egész számok. Itt megtörténhet, hogy az ${\displaystyle x}$ elemnek nincs inverze, de ${\displaystyle {\frac {x}{y}}}$ definiálható az ${\displaystyle ay=x}$ egyenlet megoldásaként.

Ferdetestek

A ferdetestek olyan gyűrűk, amikben minden nem nulla elemnek van inverze. A legegyszerűbb nem kommutatív példát a kvaterniók adják. Ha a szorzás nem kommutatív, akkor nem lehet egyetlen osztásműveletet bevezetni, mivel

${\displaystyle \left({\frac {1}{x}}\right)\left({\frac {1}{y}}\right)\neq \left({\frac {1}{y}}\right)\left({\frac {1}{x}}\right),}$

és az ${\displaystyle {\frac {x}{y}}}$ hányados nem egyértelmű.

Hatványozás

Az ismételt szorzás hatványozást eredményez. Például a ${\displaystyle 2\cdot 2\cdot 2}$ hármas szorzat 2 harmadik hatványa, és ${\displaystyle 2^{3}}$-ként írható. Ebben a példában 2 az alap, és 3 a kitevő. Általában a felső indexbe írt kitevő jelöli azt, hogy az alap hány tényezős szorzatát kell venni.

Így az a alapot n-szer szorozzuk össze:

${\displaystyle a^{n}=\underbrace {a\times a\times \cdots \times a} _{n}}$

Lásd bővebben: Hatvány

Jegyzetek

Források

• Boyer, Carl B. (revised by Merzbach, Uta C.) (1991). History of Mathematics. John Wiley and Sons, Inc. ISBN 0-471-54397-7.
• Bokor József (szerk.). A Pallas nagy lexikona. Arcanum: FolioNET (1893–1897, 1998.). ISBN 963 85923 2 X 

Kapcsolódó szócikkek

• összeadás
• kivonás

További információk

• Practicing and Learning Multiplication
• Multiplication and Arithmetic Operations In Various Number Systems at cut-the-knot
• Modern Chinese Multiplication Techniques on an Abacus
• Math Games for Multiplication
• Online számológép