Mathématiques des origamis

Pour les articles homonymes, voir Pliage (homonymie).
Les pliages d'origamis sont utilisés en mathématiques pour procéder à des constructions géométriques. Selon les méthodes de pliages utilisées, on obtient des procédés plus riches que ceux propres à la règle et au compas.
Formalisation des origamis
Le formalisme auquel il est le plus souvent fait référence est celui de Huzita. Il contient 6 axiomes qui sont en fait les 6 pliages de base permettant de décomposer n'importe quel origami. En voici la liste :
-
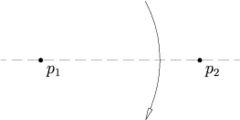 Axiome 1. Un unique pli passe par deux points et spécifiés.
Axiome 1. Un unique pli passe par deux points et spécifiés. -
 Axiome 2. Un unique pli amène un point sur un point .
Axiome 2. Un unique pli amène un point sur un point . -
 Axiome 3. Un pli superpose deux droites et .
Axiome 3. Un pli superpose deux droites et . -
 Axiome 4. Un unique pli passe par un point et est orthogonal à une droite .
Axiome 4. Un unique pli passe par un point et est orthogonal à une droite . -
 Axiome 5. Soient une droite et deux points et ; un pli passe par et amène sur .
Axiome 5. Soient une droite et deux points et ; un pli passe par et amène sur . -
 Axiome 6. Soient deux droites et et deux points et ; un pli amène sur et sur .
Axiome 6. Soient deux droites et et deux points et ; un pli amène sur et sur .
Les axiomes 1 à 4 ont toujours au moins une construction possible, unique pour les axiomes 1, 2 et 4. Les axiomes 5 et 6 peuvent n'en avoir aucune, une ou plusieurs selon la disposition des points et des droites. Ces deux derniers axiomes expriment que, lorsqu'il y a au moins une solution, alors elle peut être obtenue par origami.
Points, droites et nombres constructibles par origami
On se donne deux points de base. À partir de ces deux points, on définit récursivement les points et les lignes constructibles par origami de la façon suivante :
- Les points de base sont constructibles par hypothèse.
- Les droites construites sur les plis définis par les axiomes 1 à 6 à partir d'objets constructibles sont constructibles.
- Un point intersection de deux droites constructibles est constructible.
On appelle nombre constructible par origami un nombre égal à la distance de deux points constructibles, les deux points de base étant à une distance unité.
On peut alors interpréter les axiomes 1) à 4) de la façon suivante :
- Axiome 1. une droite passant par deux points constructibles est constructible.
- Axiome 2. la médiatrice d'un segment dont les extrémités sont constructibles est constructible.
- Axiome 3. la bissectrice de deux droites constructibles est constructible.
- Axiome 4. la perpendiculaire passant un point constructible à une droite constructible est constructible.
Les nombres constructibles au moyen de ces quatre axiomes sont exactement les mêmes que ceux qu'on peut construire avec la règle et le compas à pointes sèches. Il s'agit par exemple de ou mais ni de ni de . Voici par exemple la construction du symétrique d'un point P par rapport à une droite (L).
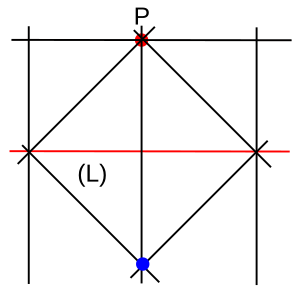
On construit la perpendiculaire à (L) passant par P puis la perpendiculaire à cette perpendiculaire passant par P (autrement dit, la parallèle à (L) passant par P). On construit les deux bissectrices en P à la parallèle à (L) et la perpendiculaire à (L). Ces deux bissectrices vont couper (L) en deux points d'où l'on trace deux nouvelles perpendiculaires à (L). Deux dernières bissectrices vont se couper en le symétrique à P cherché.
- L'axiome 5 est équivalent à chercher l'intersection d'une droite et d'un cercle.
Les nombres constructibles au moyen des cinq premiers axiomes sont exactement les mêmes que les nombres constructible à la règle et au compas.
- L'axiome 6 offre des procédés de construction particulièrement puissants. Il revient à construire la tangente aux deux paraboles de foyers et et de directrices respectives et .
L'axiome 6 permet de résoudre les équations du troisième degré et du quatrième degré à coefficients constructibles. Il permet par exemple de trisecter un angle, de dupliquer le cube ou de construire l'heptagone régulier, choses qu'on ne peut faire à la règle et au compas. L'ensemble des nombres constructibles à l'aide des six axiomes est le plus petit corps contenant les rationnels et stable par les opérations de calcul de racine carrée et de racine cubique.
Voici par exemple la construction de .

On considère un carré ABCD que l'on plie en trois. On effectue un troisième pli de façon que A soit amené sur R et E sur S. Alors CR/BR est égal à .
Origami et pliage fractal
Notons la hauteur OA et la largeur OO' d'un rectangle . Soit le point de tel que OB soit égal à . Procédons de même pour construire sur le segment .
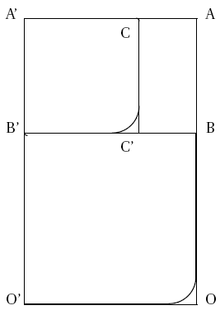
est un carré. On reporte en sur . On note son vis-à-vis sur pour y former le carré .
Il reste le rectangle ; quelles sont ses propriétés ? Voici les longueurs de quelques segments de cette figure :
- est de longueur ,
- et de longueur ,
- est donc de longueur ,
- est aussi de longueur ,
- et donc est de longueur .
Notons le rapport de la longueur sur la largeur du rectangle . On obtient : si est plus long que ou si est plus long que .
Exprimons en fonction du rapport de sur (que l'on note ) : . On obtient respectivement : ou .
Une valeur de est particulièrement intéressante, , ce qui signifie que les proportions du rectangle restant après avoir retiré les deux carrés successifs (d'abord puis ), sont les mêmes que celles du rectangle original.
Il y a deux solutions possibles : ou , qui donnent respectivement ou

Le premier cas correspond aux proportions des feuilles (par exemple , les feuilles rectangulaires standard) :
| Format | Largeur | Hauteur |
|---|---|---|
Le second cas fait apparaître le nombre d'or.
Si on itère le procédé, ces deux formats de feuilles permettent de réaliser des origamis fractales, car dans le rectangle restant, aux mêmes proportions que le premier, il est encore possible de retirer deux carrés, puis de recommencer, théoriquement jusque l'infini.
-
 pliage fractal
pliage fractal -
 pliage fractal
pliage fractal
Annexes
Sur les autres projets Wikimedia :
- Mathématiques des origamis, sur Wikimedia Commons
Articles connexes
- Nombre constructible
- Didier Boursin et ses ouvrages sur les pliages mathématiques
- Théorème de Kawasaki (en)
- Théorème de Maekawa (de)
Bibliographie
- (en) T. Sundara Row, Geometric exercices in paper folding, Dover, .
- Kôdi Husimi et Mitsue Husimi, The Geometry of Origami, Tokyo, Nihon Hyouronsha, , 2e éd. (1re éd. 1984)
- (en) David Auckly et John Cleveland, « Totally real origami and impossible paper folding », The American Mathematical Monthly, vol. 102, no 3, , p. 215-226 (DOI 10.2307/2975008, JSTOR 2975008) Les axiomes choisis par les auteurs sont équivalents aux quatre premiers axiomes de cet article
- (en) R.C. Alperin, « A mathematical theory of origami constructions and numbers », New York Journal of Mathematics, vol. 6, , p. 119-133 (lire en ligne)
- Jean-Paul Delahaye, « Les mathématiques de l'origami », Pour la Science, no 448, , p. 76-81
- (en) Shuo Ma, Muhao Chen, Hongying Zhang et Robert E. Skelton, « Statics of integrated origami and tensegrity systems », International Journal of Solids and Structures, vol. 279, , article no 112361 (DOI 10.1016/j.ijsolstr.2023.112361)
Liens externes
- (en) Trisection par pliage de papier sur le site de cut-the-knot.
- Michael Friedman — « Le pliage du papier et l’histoire des mathématiques » — Images des Mathématiques, CNRS, 2020
v · m | ||
|---|---|---|
| Étude |
|  |
| Formes, modèles |
| |
| Technique | ||
| Plieurs | ||
 Portail des arts
Portail des arts  Portail des jeux
Portail des jeux  Portail de la géométrie
Portail de la géométrie












![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)





![{\displaystyle [O,A]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eabb3e18e354d44bd6f8747d5b0d3c15eeabfb13)

![{\displaystyle [O',A']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8918c6d39eda47ee7733f56c96f9716fb9421ec)


![{\displaystyle [A,A']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf8c1d48638f584a21bdfbd5e23ff705f27d5f4)

![{\displaystyle [B,B']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8cd1021808e701e1d83e51fe643b45c0420f175)


![{\displaystyle [O,O']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4b1194d7423e8e980cc0d5c8862a1c5ece8cc13)
![{\displaystyle [O,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f2a572b505d26f6245f6154ad5a17f42a4183105)
![{\displaystyle [A,B]=[A,O]-[B,O]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b1e2fe2da7d182ae79dc2e6f57c38888872fd30)

![{\displaystyle [A',C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/789df436446cc03e5edf055afe7dd4fb3394f4da)
![{\displaystyle [A,C]=[A,A']-[C,A']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/211e0135c990fa4e6416eff41aa6e1d66f928d44)



![{\displaystyle [A,C]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/077be06e7e743c6266cd0e96d203e6666fd48661)
![{\displaystyle [A,B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1993067bb075f2ebfa02e78959b7c5bed68e06f4)





























