Graphe sommet-connexe

Cet article est une ébauche concernant les mathématiques.

Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.

En théorie des graphes, un graphe connexe « est dit k-sommet-connexe s'il possède au moins k + 1 sommets et s'il reste encore connexe après en avoir ôté k – 1^[1] ».

Définitions

Un graphe autre qu'un graphe complet est de degré de sommet-connexité k s'il est k-sommet-connexe sans être k+1-sommet-connexe, donc si k est la taille du plus petit sous-ensemble de sommets dont la suppression déconnecte le graphe^[2]. Les graphes complets ne sont pas inclus dans cette version de la définition car ils ne peuvent pas être déconnectés en supprimant des sommets. Le graphe complet à n sommets est de degré de connexité n-1.

Une définition équivalente est qu'un graphe avec au moins deux sommets est k-sommet-connexe, pour chaque paire de ses sommets, il existe est k chaînes indépendantes reliant ces sommets ; c'est le théorème de Menger^[3]. Cette définition produit la même réponse n − 1, pour la connexité du graphe complet K_n^[2].

Un graphe 1-sommet-connexe est appelé un graphe connexe ; un graphe 2-sommet-connexe est appelé un graphe biconnexe. Un graphe 3-connexe est aussi appelé triconnexe.

Un graphe régulier de degré k est au plus k-sommet-connexe et k-arête-connexe. S'il est effectivement k-sommet-connexe et k-arête-connexe, il est dit optimalement connecté.

Exemples

• Pour tout n, le graphe complet K_n (régulier de degré n – 1) est optimalement connecté.
• Pour tout k > 2 et tout j > 1, le graphe moulin Wd(k, j) est 1-sommet-connexe. Pour le séparer en j composantes connexes, il suffit de supprimer son sommet de plus haut degré : son centre.
• Le graphe cycle C_n est 2-sommet-connexe pour tout n > 3.
• Le 110-graphe de Iofinova-Ivanov est 3-sommet-connexe.

• 
  Le graphe de Biggs-Smith est 3-régulier, 3-sommet-connexe et 3-arête-connexe : il est optimalement connecté.
• 
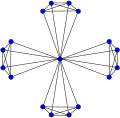  Le graphe moulin Wd(5,4) n'est plus connexe si l'on supprime son sommet central: il est 1-sommet-connexe.
• 
  Le graphe complet K₆ est 5-sommet-connexe.

Nombre de graphes selon leur sommet-connexité

Nombre de graphes simples ${\displaystyle k}$-sommet-connexes à ${\displaystyle n}$ sommets pour ${\displaystyle n}$ de 1 à 9, avec la référence à OEIS :

${\displaystyle k}$ \ ${\displaystyle n}$	1	2	3	4	5	6	7	8	9	OEIS
total	1	2	4	11	34	156	1044	12346	274668	A000088
1	1	1	2	6	21	112	853	11117	261080	A001349
2	0	1	1	3	10	56	468	7123	194066	A002218
3	0	0	1	1	3	17	136	2388	80890	A006290
4	0	0	0	1	1	4	25	384	14480	A086216
5	0	0	0	0	1	1	4	39	1051	A086217
6	0	0	0	0	0	1	1	5	59
7	0	0	0	0	0	0	1	1	5

Nombre de graphes simples exactement ${\displaystyle k}$-sommet-connexes à ${\displaystyle n}$ sommets:

${\displaystyle k}$ \ ${\displaystyle n}$	1	2	3	4	5	6	7	8	9	OEIS
0	0	1	2	5	13	44	191	1229	13588
1	1	0	1	3	11	56	385	3994	67014	A052442
2	0	1	0	2	7	39	332	4735	113176	A052443
3	0	0	1	0	2	13	111	2004	66410	A052444
4	0	0	0	1	0	3	21	345	13429	A052445
5	0	0	0	0	1	0	3	34	992
6	0	0	0	0	0	1	0	4	54

Référence

Bibliographie

• Jiří Matoušek et Jaroslav Nešetřil, Introduction aux mathématiques discrètes, Springer, 2004 (lire en ligne)
• Reinhard Diestel, Graph Theory, Springer-Verlag, coll. « Graduate Texts in Mathematics, Volume 173 », 2016, 5^e éd., 447 p. (ISBN 978-3-662-53621-6 et 978-3-96134-005-7, lire en ligne)
• Lutz Volkmann, Fundamente der Graphentheorie, Springer, 1996 (ISBN 3-211-82774-9, lire en ligne).
• Alexander Schrijver, Combinatorial optimization : Polyhedra and efficiency, Berlin, Springer, 2003, 1881 (3 volumes) (ISBN 978-3-540-44389-6)

Liens externes

• (en) Eric W. Weisstein, « k-Connected Graph », sur MathWorld

Article connexe

• Graphe arête-connexe
• Lexique de la théorie des graphes

• Portail de la géométrie
• Portail de l'informatique théorique