Différence de deux carrés

En mathématiques, la différence de deux carrés est un nombre au carré (multiplié par lui-même) soustrait d'un autre nombre au carré. Toute différence de carrés peut être factorisée selon l'identité:

${\displaystyle a^{2}-b^{2}=(a+b)(a-b)}$

en algèbre élémentaire.

Preuve

La preuve de l'identité de factorisation est simple. En partant du membre de gauche, on applique la loi distributive pour obtenir

${\displaystyle (a+b)(a-b)=a^{2}+ba-ab-b^{2}}$

Par la loi commutative, les deux termes du milieu s'annulent :

${\displaystyle ba-ab=0}$

il reste donc

${\displaystyle (a+b)(a-b)=a^{2}-b^{2}}$

L'identité qui en résulte est l'une des plus utilisées en mathématiques. Parmi de nombreuses utilisations, il donne une preuve simple de l'inégalité arithmético-géométrique à deux variables.

La preuve est valable dans tout anneau commutatif.

Inversement, si cette identité est vérifiée dans un anneau R pour toutes les paires d'éléments a et b, alors R est commutatif. Pour voir cela, on applique la loi de distribution au côté droit de l'équation et obtient:

${\displaystyle a^{2}+ba-ab-b^{2}}$ .

Pour que celui-ci soit égal à ${\displaystyle a^{2}-b^{2}}$, nous devons avoir

${\displaystyle ba-ab=0}$

donc pour tous les couples a, b, donc R est commutatif.

Démonstrations géométriques

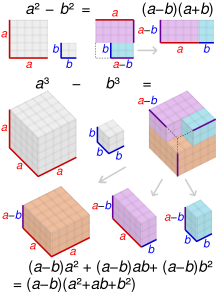
La différence de deux carrés peut également être illustrée géométriquement comme la différence de deux aires carrées dans un plan. Sur le diagramme, la partie grisée représente la différence entre les aires des deux carrés, c'est-à-dire ${\displaystyle a^{2}-b^{2}}$ . L'aire de la partie ombrée peut être trouvée en additionnant les aires des deux rectangles ; ${\displaystyle a(a-b)+b(a-b)}$, qui peut être factorisé en ${\displaystyle (a+b)(a-b)}$ . Donc, ${\displaystyle a^{2}-b^{2}=(a+b)(a-b)}$ .

Une autre preuve géométrique procède comme suit : on commence avec la figure montrée dans le premier schéma ci-dessous, un grand carré dont un plus petit carré a été retiré. Le côté du carré entier est a, et le côté du petit carré retiré est b. L'aire de la région ombrée est ${\displaystyle a^{2}-b^{2}}$ . Une coupe est effectuée, divisant la région en deux morceaux rectangulaires, comme présenté sur le deuxième schéma. La plus grande pièce, en haut, a une largeur a et une hauteur a-b. La plus petite pièce, en bas, a une largeur a-b et une hauteur b. Maintenant, la plus petite pièce peut être détachée, tournée et placée à droite de la plus grande pièce. Dans cette nouvelle disposition, illustrée dans le dernier schéma ci-dessous, les deux pièces forment ensemble un rectangle, dont la largeur est ${\displaystyle a+b}$ et dont la hauteur est ${\displaystyle a-b}$ . L'aire de ce rectangle est ${\displaystyle (a+b)(a-b)}$ . Étant donné que ce rectangle provient de la réorganisation de la figure d'origine, il doit avoir la même aire que la figure d'origine. Donc, ${\displaystyle a^{2}-b^{2}=(a+b)(a-b)}$ .

Factorisation de polynômes et simplification d'expressions

La formule de la différence de deux carrés peut être utilisée pour factoriser des polynômes qui contiennent le carré d'une première quantité moins le carré d'une deuxième quantité. Par exemple, le polynôme ${\displaystyle x^{4}-1}$ peut être factorisé comme suit :

${\displaystyle x^{4}-1=(x^{2}+1)(x^{2}-1)=(x^{2}+1)(x+1)(x-1)}$

De même, les deux premiers termes de ${\displaystyle x^{2}-y^{2}+x-y}$ peut être factorisé comme ${\displaystyle (x+y)(x-y)}$, nous avons donc:

${\displaystyle x^{2}-y^{2}+x-y=(x+y)(x-y)+x-y=(x-y)(x+y+1)}$

De plus, cette formule peut également être utilisée pour simplifier des expressions :

${\displaystyle (a+b)^{2}-(a-b)^{2}=(a+b+a-b)(a+b-a+b)=(2a)(2b)=4ab}$

Le cas des nombres complexes : la somme de deux carrés

La différence de deux carrés est utilisée pour trouver les facteurs linéaires de la somme de deux carrés, en utilisant des coefficients complexes.

Par exemple, les racines complexes de ${\displaystyle z^{2}+4}$ peuvent être trouvées en utilisant la différence de deux carrés:

${\displaystyle z^{2}+4}$

${\displaystyle =z^{2}-4i^{2}}$ (puisque ${\displaystyle i^{2}=-1}$ )

${\displaystyle =z^{2}-(2i)^{2}}$

${\displaystyle =(z+2i)(z-2i)}$

Par conséquent, les facteurs linéaires sont ${\displaystyle (z+2i)}$ et ${\displaystyle (z-2i)}$ .

Étant donné que les deux facteurs trouvés par cette méthode sont des nombres complexes conjugués, nous pouvons l'utiliser à l'envers comme méthode de multiplication d'un nombre complexe pour obtenir un nombre réel. Cette méthode est utilisée pour obtenir des dénominateurs réels dans des fractions complexes^[1].

Rationalisation des dénominateurs

La différence de deux carrés peut également être utilisée dans la rationalisation des dénominateurs irrationnels^[2]. Il s'agit d'une méthode pour supprimer les racines carrées des expressions (ou au moins les déplacer), s'appliquant à la division par certaines combinaisons impliquant des racines carrées.

Par exemple : le dénominateur de ${\displaystyle {\dfrac {5}{{\sqrt {3}}+4}}}$ peut être rationalisé comme suit :

${\displaystyle {\dfrac {5}{{\sqrt {3}}+4}}}$

${\displaystyle ={\dfrac {5}{{\sqrt {3}}+4}}\times {\dfrac {{\sqrt {3}}-4}{{\sqrt {3}}-4}}}$

${\displaystyle ={\dfrac {5({\sqrt {3}}-4)}{({\sqrt {3}}+4)({\sqrt {3}}-4)}}}$

${\displaystyle ={\dfrac {5({\sqrt {3}}-4)}{{\sqrt {3}}^{2}-4^{2}}}}$

${\displaystyle ={\dfrac {5({\sqrt {3}}-4)}{3-16}}}$

${\displaystyle =-{\dfrac {5({\sqrt {3}}-4)}{13}}.}$

Ici, le dénominateur irrationnel ${\displaystyle {\sqrt {3}}+4}$ a été rationalisé pour ${\displaystyle 13}$ .

Calcul mental

La différence de deux carrés peut également être utilisée comme raccourci arithmétique. Si deux nombres (dont la moyenne est un nombre qui est facilement élevable au carré) sont multipliés, la différence de deux carrés peut être utilisée pour donner le produit des deux nombres originaux.

Par exemple:

${\displaystyle 27\times 33=(30-3)(30+3)}$

En utilisant la différence de deux carrés, ${\displaystyle 27\times 33}$ peut être reformulé comme

${\displaystyle a^{2}-b^{2}}$ lequel est ${\displaystyle 30^{2}-3^{2}=891}$ .

Différence de deux carrés parfaits consécutifs

La différence de deux carrés parfaits consécutifs est la somme des deux bases n et n +1. Cela peut être vu comme suit :

${\displaystyle {\begin{array}{lcl}(n+1)^{2}-n^{2}&=&((n+1)+n)((n+1)-n)\\&=&2n+1\end{array}}}$

Par conséquent, la différence de deux carrés parfaits consécutifs est un nombre impair. De même, la différence de deux carrés parfaits arbitraires est calculée comme suit :

${\displaystyle {\begin{array}{lcl}(n+k)^{2}-n^{2}&=&((n+k)+n)((n+k)-n)\\&=&k(2n+k)\end{array}}}$

Par conséquent, la différence de deux carrés parfaits pairs est un multiple de 4 et la différence de deux carrés parfaits impairs est un multiple de 8.

Factorisation d'entiers

En théorie des nombres et en cryptographie, plusieurs algorithmes utilisent des différences de carrés pour trouver des facteurs d'entiers et détecter des nombres composés. Un exemple simple est la méthode de factorisation de Fermat, qui considère la séquence de nombres ${\displaystyle x_{i}:=a_{i}^{2}-N}$, pour ${\displaystyle a_{i}:=\left\lceil {\sqrt {N}}\right\rceil +i}$ . Si l'un des ${\displaystyle x_{i}}$ est égal à un carré parfait ${\displaystyle b^{2}}$, alors ${\displaystyle N=a_{i}^{2}-b^{2}=(a_{i}+b)(a_{i}-b)}$ est une factorisation (potentiellement non triviale) de ${\displaystyle N}$ .

Cette astuce peut être généralisée comme suit. Si ${\displaystyle a^{2}\equiv b^{2}}$ mod ${\displaystyle N}$ et ${\displaystyle a\not \equiv \pm b}$ mod ${\displaystyle N}$, alors ${\displaystyle N}$ est composé de facteurs non triviaux ${\displaystyle PGCD(a-b,N)}$ et ${\displaystyle PGCD(a+b,N)}$ . Cela constitue la base de plusieurs algorithmes de factorisation (tels que le crible quadratique ) et peut être combiné avec le test de primalité de Fermat pour donner le test de primalité Miller-Rabin, plus fort.

Généralisations

L'identité est également valable dans les espaces préhilbertiens sur le champ des nombres réels, comme pour le produit scalaire des vecteurs euclidiens :

${\displaystyle {\mathbf {a} }\cdot {\mathbf {a} }-{\mathbf {b} }\cdot {\mathbf {b} }=({\mathbf {a} }+{\mathbf {b} })\cdot ({\mathbf {a} }-{\mathbf {b} })}$

La preuve est identique. Pour le cas particulier où a et b ont des normes égales (ce qui signifie leurs produits scalaires sont égaux, car ${\displaystyle a\cdot a=\parallel a\parallel \times \parallel a\parallel \times \cos(a,a)=\parallel a\parallel ^{2}}$), cela démontre analytiquement le fait que deux diagonales d'un losange sont perpendiculaires. Cela découle du fait que le membre de gauche de l'équation est égal à zéro, nécessitant que le membre de droite soit également égal à zéro, et donc le produit scalaire de la somme vectorielle de a + b (la longue diagonale du losange) avec la différence vectorielle a - b ( la petite diagonale du losange) doit être égal à zéro, ce qui indique que les diagonales sont perpendiculaires.

Différence de deux nièmes puissances

Si a et b sont deux éléments d'un anneau commutatif R, alors ${\displaystyle a^{n}-b^{n}=\left(a-b\right)\left(\sum _{k=0}^{n-1}a^{n-1-k}b^{k}\right)}$ .

Histoire

Historiquement, les Babyloniens utilisaient la différence de deux carrés pour calculer les multiplications^[3].

Par exemple:

93 x 87 = 90² - 3² = 8091

64 x 56 = 60² - 4² = 3584

Articles connexes

• Congruum, la différence partagée de trois carrés dans la progression arithmétique
• Conjugué (algèbre)
• Factorisation

Remarques

Références

• James Stuart Stanton, Encyclopedia of Mathematics, Infobase Publishing, 2005 (ISBN 0-8160-5124-0, lire en ligne), p. 131
• Alan S. Tussy et Roy David Gustafson, Elementary Algebra, Cengage Learning, 2011, 467–469 p. (ISBN 978-1-111-56766-8, lire en ligne)

Liens externes

• différence de deux carrés sur mathpages.com

• Portail des mathématiques