Número poligonal centrado

Números poligonales centrados
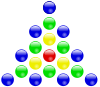Construcción de los cuatro primeros tipos de números poligonales centrados: números triangulares, cuadrangulares, pentagonales y hexagonales

Los números poligonales centrados son una clase de series de números figurados, cada uno formado por un punto central, rodeado por capas poligonales con un número constante de lados. Cada lado de una capa poligonal contiene un punto más que un lado en la capa anterior, por lo que a partir de la segunda capa poligonal, cada capa de un número k-gonal centrado contiene k más puntos que la capa anterior.

Ejemplos

Cada elemento de la secuencia es un múltiplo del número triangular anterior más 1. Esto se puede formalizar con la ecuación ${\displaystyle {\frac {ax(x+1)}{2}}+1}$ donde a es el número de lados del polígono y x es el número en la secuencia, comenzando con cero para el 1. Por ejemplo, los números cuadrados centrados son cuatro veces los números triangulares más 1, o equivalentemente ${\displaystyle {\frac {4x(x+1)}{2}}+1}$.

Estas series constan de

• Números triangulares centrados 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, ... (A005448)
• Números cuadrados centrados 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, ... (A001844)
• Números pentagonales centrados 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, ... (A005891)
• Números hexagonales centrados 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, ... (A003215), que son exactamente la diferencia de cubos consecutivos, es decir, x³ - (x-1)³
• Números heptagonales centrados 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, ... (A069099)
• Números octogonales centrados 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, ... (A016754), que son exactamente los cuadrados impares
• Números nonagonales centrados 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, ... (A060544), entre los que figuran todos los números perfectos pares excepto el 6
• Números decagonales centrados 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, ... (A062786)
• Números hendecagonales centrados 1, 12, 34, 67, 111, 166, 232, 309, 397, 496, 606, 727, ... (A069125)
• Números dodecagonales centrados 1, 13, 37, 73, 121, 181, 253, 337, 433, 541, 661, 793, ... (A003154), que también son números estrella
• ...

Números cuadrados centrados

1		5		13		25

Números hexagonales centrados

1		7		19		37

Fórmulas

Como se puede ver en los diagramas anteriores, el n-ésimo número centrado en un polígono k-gonal se puede obtener colocando k copias del (n−1)-ésimo número triangular alrededor de un punto central; por lo tanto, el n-ésimo número k-gonal centrado se puede representar matemáticamente por

${\displaystyle C_{k,n}={\frac {kn}{2}}(n-1)+1.}$

La diferencia de los números n-ésimo y (n+1)-ésimo consecutivos k-gonales centrados es k(2n+1).

El n-ésimo número k-gonal centrado es igual al n-ésimo número k-gonal regular más (n-1)².

Al igual que en el caso de los números poligonales regulares, el primer número k-gonal centrado es 1. Por lo tanto, para cualquier k, 1 es tanto k-gonal como k-gonal centrado. El siguiente número que será tanto k-gonal como k-gonal centrado se puede encontrar usando la fórmula:

${\displaystyle {\frac {k^{2}}{2}}(k-1)+1}$

lo que muestra que 10 es triangular y triangular centrado, 25 es cuadrado y cuadrado centrado, etc.

Mientras que un número primo p no puede ser un número poligonal (excepto en el caso trivial, es decir, cuando p es el segundo número p-gonal), muchos números poligonales centrados son primos. De hecho, si k≥3, k≠8, k≠9, entonces hay infinitos números k-gonales centrados que son primos (asumiendo la conjetura de Buniakovski). Dado que todos los números octogonales centrados son también cuadrados perfectos, y todos los números nonagonales centrados también son números triangulares (y no son iguales a 3), ambos no pueden ser números primos.

Suma de los recíprocos

El sumatorio de inversos para las series de números k-gonales centrados es^[1]​

${\displaystyle {\frac {2\pi }{k{\sqrt {1-{\frac {8}{k}}}}}}\tan \left({\frac {\pi }{2}}{\sqrt {1-{\frac {8}{k}}}}\right)}$, si k ≠ 8

${\displaystyle {\frac {\pi ^{2}}{8}}}$, si k = 8

Referencias

Bibliografía

• Neil Sloane & Simon Plouffe (1995). The Encyclopedia of Integer Sequences. San Diego: Academic Press. : Figura M3826
• Weisstein, Eric W. «Centered polygonal number». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• F. Tapson (1999). The Oxford Mathematics Study Dictionary (2nd edición). Oxford University Press. pp. 88–89. ISBN 0-19-914-567-9.