Hipopoda

En geometría, una hipopoda (del griego antiguo ἱπποπέδη, vínculo para inmovilizar las patas de un caballo) es un curva plana determinada por una ecuación de la forma

${\displaystyle (x^{2}+y^{2})^{2}=cx^{2}+dy^{2}}$,

donde se supone que c > 0 y que c > d, ya que los casos restantes se reducen a un solo punto o se pueden expresar en la forma dada mediante una rotación. Las hipopodas son curvas algebraicas racionales bicirculares de grado 4, simétricas con respecto a los ejes x e y.

Casos especiales

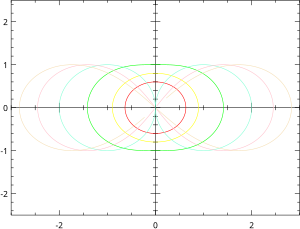
• Cuando d > 0, la curva tiene una forma ovalada y se conoce a menudo como óvalo de Booth.
• Cuando d < 0, la curva se asemeja a una figura con forma de ocho, o lemniscata, y en ocasiones se denomina lemniscata de Booth (ambas en referencia al matemático del siglo XIX James Booth, que estudió estas curvas).
• Las hipopodas también fueron investigadas por Proclo (por lo que a veces también se las llama Hipopodas de Proclo) y Eudoxo. Para d = −c, la hipopoda se corresponde con la lemniscata de Bernoulli.

Definición como secciones espíricas

Las hipopodas se pueden definir como la curva formada por la intersección de un toro y un plano, donde el plano es paralelo al eje del toro y tangente a él en el círculo interior. Por lo tanto, es un spira de Perseo que a su vez es un tipo de sección tórica.

Si se gira un círculo con radio a alrededor de un eje a la distancia b desde su centro, entonces la ecuación de la hipopoda resultante en coordenadas polares es

${\displaystyle r^{2}=4b(a-b\operatorname {sen} ^{2}\theta )}$

o en coordenadas cartesianas

${\displaystyle (x^{2}+y^{2})^{2}+4b(b-a)(x^{2}+y^{2})=4b^{2}x^{2}}$.

Debe tenerse en cuenta que cuando a > b, el toro se interseca a sí mismo, por lo que no se parece a la imagen habitual de un toro.

Véase también

• Anexo:Lista de curvas
• Toro (geometría)
• Lemniscata
• Óvalo de Cassini
• Spira de Perseo

Referencias

• Lawrence JD. (1972) Catálogo de curvas planas especiales , Dover. Pp. 145 & ndash; 146.
• Booth J. Un tratado sobre algunos nuevos métodos geométricos , Longmans, Green, Reader y Dyer, Londres, vol. I (1873) y vol. II (1877).
• Weisstein, Eric W. «Hippopede». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• "Hippopede" en 2dcurves.com
• "Courbes de Booth" en la Encyclopédie des Formes Mathématiques Remarquables

Enlaces externos

• "The Hippopede of Proclus" en The National Curve Bank