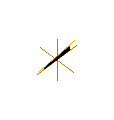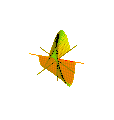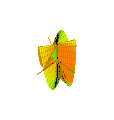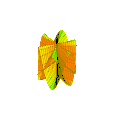Plücker's conoid



In geometry, Plücker's conoid is a ruled surface named after the German mathematician Julius Plücker. It is also called a conical wedge or cylindroid; however, the latter name is ambiguous, as "cylindroid" may also refer to an elliptic cylinder.
Plücker's conoid is the surface defined by the function of two variables:
This function has an essential singularity at the origin.
By using cylindrical coordinates in space, we can write the above function into parametric equations
Thus Plücker's conoid is a right conoid, which can be obtained by rotating a horizontal line about the z-axis with the oscillatory motion (with period 2π) along the segment [–1, 1] of the axis (Figure 4).
A generalization of Plücker's conoid is given by the parametric equations
where n denotes the number of folds in the surface. The difference is that the period of the oscillatory motion along the z-axis is 2π/n. (Figure 5 for n = 3)


-
 Animation of Plucker's conoid with n = 2
Animation of Plucker's conoid with n = 2 -
 Plucker's conoid with n = 2
Plucker's conoid with n = 2 -
 Plucker's conoid with n = 3
Plucker's conoid with n = 3 -
 Animation of Plucker's conoid with n = 2
Animation of Plucker's conoid with n = 2 -
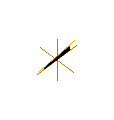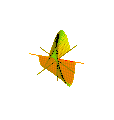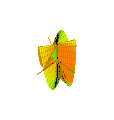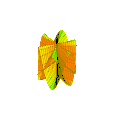 Animation of Plucker's conoid with n = 3
Animation of Plucker's conoid with n = 3 -
 Plucker's conoid with n = 4
Plucker's conoid with n = 4
See also
- Ruled surface
- Right conoid
- Wallis's conical edge
References
- A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, Florida:CRC Press, 2006. [1] (ISBN 978-1-58488-448-4)
- Vladimir Y. Rovenskii, Geometry of curves and surfaces with MAPLE [2] (ISBN 978-0-8176-4074-3)
External links
- Weisstein, Eric W. "Plücker's Conoid". MathWorld.
- v
- t
- e