Metallic mean

Gold, silver, and bronze ratios within their respective rectangles.

The metallic mean (also metallic ratio, metallic constant, or noble means^[1]) of a natural number n is a positive real number, denoted here ${\displaystyle S_{n},}$ that satisfies the following equivalent characterizations:

• the unique positive real number ${\displaystyle x}$ such that ${\textstyle x=n+{\frac {1}{x}}}$
• the positive root of the quadratic equation ${\displaystyle x^{2}-nx-1=0}$
• the number ${\textstyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}}$
• the number whose expression as a continued fraction is

  ${\displaystyle [n;n,n,n,n,\dots ]=n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+\ddots \,}}}}}}}}}$

Metallic means are generalizations of the golden ratio (${\displaystyle n=1}$) and silver ratio (${\displaystyle n=2}$), and share some of their interesting properties. The term "bronze ratio" (${\displaystyle n=3}$), and terms using other metals names (such as copper or nickel), are occasionally used to name subsequent metallic means.^{[2] [3]}

In terms of algebraic number theory, the metallic means are exactly the real quadratic integers that are greater than ${\displaystyle 1}$ and have ${\displaystyle -1}$ as their norm.

The defining equation ${\displaystyle x^{2}-nx-1=0}$ of the nth metallic mean is the characteristic equation of a linear recurrence relation of the form ${\displaystyle x_{k}=nx_{k-1}+x_{k-2}.}$ It follows that, given such a recurrence the solution can be expressed as

${\displaystyle x_{k}=aS_{n}^{k}+b\left({\frac {-1}{S_{n}}}\right)^{k},}$

where ${\displaystyle S_{n}}$ is the nth metallic mean, and a and b are constants depending only on ${\displaystyle x_{0}}$ and ${\displaystyle x_{1}.}$ Since the inverse of a metallic mean is less than 1, this formula implies that the quotient of two consecutive elements of such a sequence tends to the metallic mean, when k tends to the infinity.

For example, if ${\displaystyle n=1,}$ ${\displaystyle S_{n}}$ is the golden ratio. If ${\displaystyle x_{0}=0}$ and ${\displaystyle x_{1}=1,}$ the sequence is the Fibonacci sequence, and the above formula is Binet's formula. If ${\displaystyle n=1,x_{0}=2,x_{1}=1}$ one has the Lucas numbers. If ${\displaystyle n=2,}$ the metallic mean is called the silver ratio, and the elements of the sequence starting with ${\displaystyle x_{0}=0}$ and ${\displaystyle x_{1}=1}$ are called the Pell numbers. The third metallic mean is sometimes called the "bronze ratio".

Geometry

Golden ratio within the pentagram (φ = red/ green = green/blue = blue/purple) and silver ratio within the octagon.

The defining equation ${\textstyle x=n+{\frac {1}{x}}}$ of the nth metallic mean induces the following geometrical interpretation.

Consider a rectangle such that the ratio of its length L to its width W is the nth metallic ratio. If one remove from this rectangle n squares of side length W, one gets a rectangle similar to the original rectangle; that is, a rectangle with the same ratio of the length to the width (see figures).

The nth metallic ratio is the arithmetic mean of the hypothenuse and the shortest leg of a right triangle with side lengths of 2 and n. This results from the value ${\displaystyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}}$ and the Pythagorean theorem.

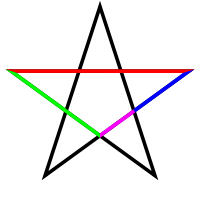
Some metallic means appear as segments in the figure formed by a regular polygon and its diagonals. This is in particular the case for the golden ratio and the pentagon, and for the silver ratio and the octagon; see figures.

Powers

Denoting by ${\displaystyle S_{m}}$ the metallic mean of m one has

${\displaystyle S_{m}^{n}=K_{n}S_{m}+K_{n-1},}$

where the numbers ${\displaystyle K_{n}}$ are defined recursively by the initial conditions K₀ = 0 and K₁ = 1, and the recurrence relation

${\displaystyle K_{n}=mK_{n-1}+K_{n-2}.}$

Proof: The equality is immediately true for ${\displaystyle n=1.}$ The recurrence relation implies ${\displaystyle K_{2}=m,}$ which makes the equality true for ${\displaystyle k=2.}$ Supposing the equality true up to ${\displaystyle n-1,}$ one has

${\displaystyle {\begin{aligned}S_{m}^{n}&=mS_{m}^{n-1}+S_{m}^{n-2}&&{\text{(defining equation)}}\\&=m(K_{n-1}S_{n}+K_{n-2})+(K_{n-2}S_{m}+K_{n-3})&&{\text{(recurrence hypothesis)}}\\&=(mK_{n-1}+K_{n-2})S_{n}+(mK_{n-2}+K_{n-3})&&{\text{(regrouping)}}\\&=K_{n}S_{m}+K_{n-1}&&{\text{(recurrence on }}K_{n}).\end{aligned}}}$

End of the proof.

One has also ^{[citation needed]}

${\displaystyle K_{n}={\frac {S_{m}^{n+1}-(m-S_{m})^{n+1}}{\sqrt {m^{2}+4}}}.}$

The odd powers of a metallic mean are themselves metallic means. More precisely, if n is an odd natural number, then ${\displaystyle S_{m}^{n}=S_{M_{n}},}$ where ${\displaystyle M_{n}}$ is defined by the recurrence relation ${\displaystyle M_{n}=mM_{n-1}+M_{n-2}}$ and the initial conditions ${\displaystyle M_{0}=2}$ and ${\displaystyle M_{1}=m.}$

Proof: Let ${\displaystyle a=S_{m}}$ and ${\displaystyle b=-1/S_{m}.}$ The definition of metallic means implies that ${\displaystyle a+b=m}$ and ${\displaystyle ab=-1.}$ Let ${\displaystyle M_{n}=a^{n}+b^{n}.}$ Since ${\displaystyle a^{n}b^{n}=(ab)^{n}=-1}$ if n is odd, the power ${\displaystyle a^{n}}$ is a root of ${\displaystyle x^{2}-M_{n}-1=0.}$ So, it remains to prove that ${\displaystyle M_{n}}$ is an integer that satisfies the given recurrence relation. This results from the identity

${\displaystyle {\begin{aligned}a^{n}+b^{n}&=(a+b)(a^{n-1}+b^{n-1})-ab(a^{n-2}+a^{n-2})\\&=m(a^{n-1}+b^{n-1})+(a^{n-2}+a^{n-2}).\end{aligned}}}$

This completes the proof, given that the initial values are easy to verify.

In particular, one has

${\displaystyle {\begin{aligned}S_{m}^{3}&=S_{m^{3}+3m}\\S_{m}^{5}&=S_{m^{5}+5m^{3}+5m}\\S_{m}^{7}&=S_{m^{7}+7m^{5}+14m^{3}+7m}\\S_{m}^{9}&=S_{m^{9}+9m^{7}+27m^{5}+30m^{3}+9m}\\S_{m}^{11}&=S_{m^{11}+11m^{9}+44m^{7}+77m^{5}+55m^{3}+11m}\end{aligned}}}$

and, in general,^{[citation needed]}

${\displaystyle S_{m}^{2n+1}=S_{M},}$

where

${\displaystyle M=\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}m^{2k+1}.}$

For even powers, things are more complicate. If n is a positive even integer then^{[citation needed]}

${\displaystyle {S_{m}^{n}-\left\lfloor S_{m}^{n}\right\rfloor }=1-S_{m}^{-n}.}$

Additionally,^{[citation needed]}

${\displaystyle {1 \over {S_{m}^{4}-\left\lfloor S_{m}^{4}\right\rfloor }}+\left\lfloor S_{m}^{4}-1\right\rfloor =S_{\left(m^{4}+4m^{2}+1\right)}}$

${\displaystyle {1 \over {S_{m}^{6}-\left\lfloor S_{m}^{6}\right\rfloor }}+\left\lfloor S_{m}^{6}-1\right\rfloor =S_{\left(m^{6}+6m^{4}+9m^{2}+1\right)}.}$

Generalization

One may define the metallic mean ${\displaystyle S_{-n}}$ of a negative integer −n as the positive solution of the equation ${\displaystyle x^{2}-(-n)-1.}$ The metallic mean of −n is the multiplicative inverse of the metallic mean of n:

${\displaystyle S_{-n}={\frac {1}{S_{n}}}.}$

Another generalization consists of changing the defining equation from ${\displaystyle x^{2}-nx-1=0}$ to ${\displaystyle x^{2}-nx-c=0}$. If

${\displaystyle R={\frac {n\pm {\sqrt {n^{2}+4c}}}{2}},}$

is any root of the equation, one has

${\displaystyle R-n={\frac {c}{R}}.}$

The silver mean of m is also given by the integral^{[citation needed]}

${\displaystyle S_{m}=\int _{0}^{m}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{m+2} \over {2m}}\right)}\,dx.}$

Another form of the metallic mean is^{[citation needed]}

${\displaystyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}=e^{\operatorname {arsinh(n/2)} }.}$

Numerical values

See also

• Constant
• Mean
• Ratio
• Plastic ratio

Notes

References

Further reading

• Stakhov, Alekseĭ Petrovich (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science, p. 228, 231. World Scientific. ISBN 9789812775832.

External links

• Cristina-Elena Hrețcanu and Mircea Crasmareanu (2013). "Metallic Structures on Riemannian Manifolds", Revista de la Unión Matemática Argentina.
• Rakočević, Miloje M. "Further Generalization of Golden Mean in Relation to Euler's 'Divine' Equation", Arxiv.org.

• v
• t
• e

Metallic means

• Pisot number
• Gold
  • Angle
  • Base
  • Fibonacci sequence
  • Kepler triangle
  • Rectangle
  • Rhombus
  • Section search
  • Spiral
  • Triangle

• Silver
  • Pell number
• Bronze
• Copper
• Nickel
• etc...