Zentrierte Dreieckszahl

19 Kugeln in Form ineinandergeschachtelter Dreiecke

Eine zentrierte Dreieckszahl ist eine Zahl, die sich nach der Formel

3 n 2 − 3 n + 2 2 {\displaystyle {\frac {3n^{2}-3n+2}{2}}}

aus einer natürlichen Zahl n {\displaystyle n} berechnen lässt. Die ersten zentrierten Dreieckszahlen sind

1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, … (Folge A005448 in OEIS)

Die zentrierten Dreieckszahlen gehören wie die zentrierten Quadratzahlen sowie die zentrierten Fünf- und Sechseckszahlen zu den zentrierten Polygonalzahlen, also zu den ebenen figurierten Zahlen.

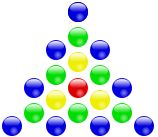
Die zentrierten Dreieckszahlen beziffern nämlich die Anzahl von Steinchen, um ein Dreieck nach folgender Vorschrift zu legen: Es befindet sich ein Steinchen im Zentrum und um dieses werden in dreiecksförmigen Schichten mit steigender Seitenlänge weitere Steinchen angeordnet. Die Anzahl der Steinchen in einer solchen Anordnung mit n {\displaystyle n} Schichten wird als ( n + 1 ) {\displaystyle (n+1)} -te zentrierte Dreieckszahl bezeichnet.

Für n ≥ 3 {\displaystyle n\geq 3} lässt sich jede zentrierte Dreieckszahl als die Summe dreier aufeinanderfolgender normaler Dreieckszahlen Δ n − 2 + Δ n − 1 + Δ n {\displaystyle \Delta _{n-2}+\Delta _{n-1}+\Delta _{n}} darstellen. Des Weiteren gilt, dass eine Ganzzahldivision einer beliebigen zentrierten Dreieckszahl Z D n {\displaystyle ZD_{n}} durch 3 immer den Rest 1 ergibt und als Quotient die vorhergehende Dreieckszahl Δ n − 1 {\displaystyle \Delta _{n-1}} .

Die Summe der ersten n zentrierten Dreieckszahlen (n ≥ 3) ergibt die magische Konstante (Zeilensumme) eines magischen Quadrates der Zahlen 1 bis n².

Unendliche Summen und Produkte

Die unendliche Summe der Kehrwerte der zentrierten Dreieckszahlen ergibt diesen Wert:

∑ n = 1 ∞ 1 Z D n = ∑ n = 1 ∞ 2 3 n 2 − 3 n + 2 = 2 15 π tanh ⁡ ( 1 6 15 π ) {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{ZD_{n}}}=\sum _{n=1}^{\infty }{\frac {2}{3n^{2}-3n+2}}={\frac {2}{\sqrt {15}}}\pi \tanh {\bigl (}{\frac {1}{6}}{\sqrt {15}}\pi {\bigr )}}

Das unendliche Produkt von den Quotienten der verdoppelten zentrierten Dreieckszahlen dividiert durch die zentrierten Sechseckszahlen an denselben Positionen ergibt jenen Wert:

∏ n = 1 ∞ 2 Z D n Z S n = ∏ n = 1 ∞ 3 n 2 − 3 n + 2 3 n 2 − 3 n + 1 = sech ⁡ ( 1 6 3 π ) cosh ⁡ ( 1 6 15 π ) {\displaystyle \prod _{n=1}^{\infty }{\frac {2ZD_{n}}{ZS_{n}}}=\prod _{n=1}^{\infty }{\frac {3n^{2}-3n+2}{3n^{2}-3n+1}}=\operatorname {sech} {\bigl (}{\frac {1}{6}}{\sqrt {3}}\pi {\bigr )}\cosh {\bigl (}{\frac {1}{6}}{\sqrt {15}}\pi {\bigr )}}

Zentrierte Dreiecksprimzahlen

Eine zentrierte Dreieckszahl, die eine Primzahl ist, wird als zentrierte Dreiecksprimzahl bezeichnet. Die ersten zentrierten Dreiecksprimzahlen lauten:

19, 31, 109, 199, 409, … (Folge A125602 in OEIS)

Siehe auch

  • Polygonalzahl

Literatur

  • Lancelot Hogben: Mathematik für alle. Eine Einführung in die Wissenschaft der Zahlen und Figuren. Neu überarbeitete Ausgabe. Pawlak, Herrsching 1985, ISBN 3-88199-208-1, S. 151 ff.

Weblinks

  • Eric W. Weisstein: centered triangular number. In: MathWorld (englisch).