Malfatti-Kreis

Die Malfatti-Kreise, später bekannt als Malfattisches Problem,^[1] sind benannt nach Gianfrancesco Malfatti, der 1803 ihre Konstruktion angab.^[2] Bestimmt sind die Malfatti-Kreise – unabhängig von der Form des Ausgangsdreiecks – durch drei Kreise in einem Dreieck mit der Eigenschaft, dass jeder die beiden anderen Kreise von außen und zwei Dreiecksseiten von innen berührt.^[3][4]

Malfatti nahm fälschlich an, dass diese Eigenschaft der Kreise das Problem löse, drei Kreise überschneidungsfrei so in ein Dreieck zu packen, dass sie maximalen Flächeninhalt haben. Warum die Malfatti-Kreise dieses sogenannte Malfatti’sche Maximierungsproblem, sprich die maximale Bedeckung der Dreiecksfläche durch drei Kreise, nicht lösen, lässt sich z. B. leicht an einem langen schmalen rechtwinkligen Dreieck erkennen.^[5]

Für die Radien der Malfatti-Kreise eines Dreiecks ABC gilt:^[6]

${\displaystyle r_{A}={\frac {r}{2(s-a)}}(s-r-({\overline {IB}}+{\overline {IC}}-{\overline {IA}}))}$

${\displaystyle r_{B}={\frac {r}{2(s-b)}}(s-r-({\overline {IC}}+{\overline {IA}}-{\overline {IB}}))}$

${\displaystyle r_{C}={\frac {r}{2(s-c)}}(s-r-({\overline {IA}}+{\overline {IB}}-{\overline {IC}}))}$

Dabei steht ${\displaystyle r}$ für den Inkreisradius und ${\displaystyle s}$ für den halben Dreiecksumfang. ${\displaystyle I}$ ist der Inkreismittelpunkt und ${\displaystyle \omega _{\alpha },\omega _{\beta },\omega _{\gamma }}$ sind die drei Winkelhalbierenden.

Geschichtliches

Das ursprüngliche Malfatti-Problem bezog sich auf eine Aufgabe aus der Stereotomie,^[6] deren vermeintliche Lösung Malfatti 1802 fand und 1803 in der Memoria di Matematica e Fisica della Società Italiana delle Scienze in seinem Artikel Memoria sopra un problema stereotomico veröffentlichte. Zu Beginn seines Artikels formuliert Malfatti dazu die Aufgabenstellung.^[6]

Frei übersetzt lautet sie:

Aus einem gegebenen rechtwinkligen Prisma aus beliebigem Material, z. B. Marmor, schneide daraus drei [kreisförmige] Zylinder mit der gleichen Höhe wie das Prisma, aber mit dem maximalen Gesamtvolumen, d. h. mit der minimalen Materialverschwendung aus dem Volumen des Prismas.

In seinem Artikel Memoria sopra un problema stereotomico weist Malfatti auch darauf hin, dass diese stereotomische Aufgabe auf ein Problem der Flächengeometrie reduzierbar ist. Er definiert die Lage der Kreise, die dem Dreieck einbeschrieben sind, heute als Malfatti-Kreise bezeichnet, folgendermaßen:^[6]

Freie Übersetzung

Gegeben sei ein Dreieck, konstruiere drei Kreise darin so, dass jeder der Kreise tangential ist (das heißt, sie berühren einen Punkt) mit den anderen zwei und mit zwei Seiten des Dreiecks.

Das wurde allerdings 1992 von W. A. Salgaller und G. A. Los^[7] widerlegt,^[8] die zeigten, dass die Lösung stattdessen dadurch erreicht wird, jeweils in aufeinanderfolgenden Schritten einen Kreis mit dem größten Flächeninhalt einzubeschreiben – im Folgenden beschrieben im Abschnitt Konstruktion nach Salgaller und Los.

Bereits 1687 wurde das Malfatti-Konstruktionsproblem von Jakob I Bernoulli in einem Spezialfall gelöst (gleichschenkliges Dreieck)^[9][10] und später gaben Jakob Steiner^[11][12] auf rein geometrischem Weg^[9] und Alfred Clebsch Lösungen, Letzterer mit elliptischen Funktionen (1857, Crelle’s Journal).^[13] Auch der Japaner Ajima Naonobu gab 30 Jahre vor Malfatti im Rahmen japanischer Architektur eine Lösung.^[14] Dass die Konstruktion von Malfatti das Malfatti-Problem nicht in allen Fällen löste, zeigten schon Lob und Richmond 1930 mithilfe gleichseitiger Dreiecke^[15] sowie Howard W. Eves 1965 durch Untersuchungen anhand schmaler und langer Dreiecke.^[5] Im Jahr 1967 wurde sogar von Michael Goldberg in einem Aufsatz gezeigt,^[16] dass Malfattis Konstruktion dies in keinem Fall tut. Hierfür erbrachten, wie bereits oben erwähnt, Salgaller und Los 1992 die Lösung. Die Begründung von Salgaller und Los war aber nicht vollständig und auf reine numerische rechnerische Argumenten in manchen Schwerpunkten basiert (wie bei Goldberg 1967). Im Juni 2022 hat Giancarlo Lombardi dazu den ersten geometrisch-analytischen Beweis durchgeführt und somit die Lösung erledigt.^[17]

Freie Übersetzung (Teil der Zusammenfassung)

Geometrische Konstruktionen

Ingmar Lehmann erläutert 2003 diverse Lösungen des Malfatti-Problems in seiner Analyse Das Malfatti-Problem – Ein Thema in der Begabtenförderung. Im Folgenden werden daraus vier Methoden im Einzelnen beschrieben.

Konstruktion nach Malfatti

Variante mit vorherigen Berechnungen

Dazu leitet Lehmann mithilfe des Satzes des Pythagoras und der Ähnlichkeit von Dreiecken drei Gleichungen her, deren Lösungen die Tangentenabschnitte ${\displaystyle x\;={\overline {AC_{1}}},\;y={\overline {BC_{2}}}}$ und ${\displaystyle z={\overline {CA_{2}}}}$ liefern.

Es werden noch folgende Beziehungen berücksichtigt:

${\displaystyle {\overline {AI}}={\sqrt {r^{2}+s^{2}}},\;\;\;{\overline {BI}}={\sqrt {r^{2}+t^{2}}},\;\;\;{\overline {CI}}={\sqrt {r^{2}+u^{2}}},}$

darin bedeuten die Bezeichnungen

${\displaystyle s={\overline {AL_{c}}},\;t={\overline {BL_{c}}}}$ und ${\displaystyle u={\overline {CL_{a}}}.}$

Mit den entsprechend eingesetzten Werten ist es jetzt möglich, eine sogenannte Hilfsstrecke ${\displaystyle {\overline {PQ}}}$ mit der Länge ${\displaystyle m}$ zu bestimmen

${\displaystyle m={\frac {1}{2}}\left({\overline {AI}}+{\overline {BI}}+{\overline {CI}}-{\overline {AL_{c}}}-{\overline {BL_{c}}}-{\overline {CL_{a}}}+r\right),}$

dann gilt für die oben beschriebenen Tangentenabschnitte

${\displaystyle x={\overline {AC_{1}}}={\overline {AI}}-m,\;\;\;y={\overline {BC_{2}}}={\overline {BI}}-m,\;\;\;z={\overline {CA_{2}}}={\overline {CI}}-m.}$

Wird in der Formel für ${\displaystyle m}$ der Faktor ${\displaystyle {\frac {1}{2}}}$ den Summanden einzeln zugeordnet

${\displaystyle m={\frac {1}{2}}{\overline {AI}}+{\frac {1}{2}}{\overline {BI}}+{\frac {1}{2}}{\overline {CI}}-{\frac {1}{2}}{\overline {AL_{c}}}-{\frac {1}{2}}{\overline {BL_{c}}}-{\frac {1}{2}}{\overline {CL_{a}}}+{\frac {1}{2}}r,}$

ist damit eine sehr einfache und platzsparende geometrische Konstruktion (siehe nebenstehendes Bild) darstellbar.

Konstruktionsbeschreibung

Nach dem Zeichnen eines z. B. ungleichseitigen Dreiecks ${\displaystyle ABC}$ mit den Seitenlängen ${\displaystyle a,\;b}$ und ${\displaystyle c}$ wird der Mittelpunkt des Inkreises ${\displaystyle I}$ mithilfe der drei Winkelhalbierenden ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ und ${\displaystyle \omega _{\gamma }}$ bestimmt. Damit ergeben sich die Strecken ${\displaystyle {\overline {AI}},{\overline {BI}}}$ und ${\displaystyle {\overline {CI}}.}$ Es folgt das Fällen des Lots von ${\displaystyle I}$ auf die Strecke ${\displaystyle {\overline {BC}}}$ mit dem Fußpunkt ${\displaystyle L_{a}}$ und das Ziehen des Inkreises ${\displaystyle k}$ um ${\displaystyle I}$ mit dem Radius ${\displaystyle {\overline {IL_{a}}}.}$ Das Fällen der Lote von ${\displaystyle I}$ auf ${\displaystyle {\overline {AC}}}$ mit dem Fußpunkt ${\displaystyle L_{b}}$ sowie von ${\displaystyle I}$ auf ${\displaystyle {\overline {AB}}}$ mit dem Fußpunkt ${\displaystyle L_{c}}$ schließt sich an.

Nun wird die Länge ${\displaystyle m}$ der Hilfsstrecke ${\displaystyle {\overline {PQ}}}$ folgendermaßen auf einer Zahlengeraden ermittelt. Zuerst werden die Streckenhälften ${\displaystyle {\frac {1}{2}}{\overline {AI}},\;{\frac {1}{2}}{\overline {BI}}}$ und ${\displaystyle {\frac {1}{2}}{\overline {CI}}}$ addiert, aus deren Summe die Streckenhälften ${\displaystyle {\frac {1}{2}}{\overline {AL_{c}}},\;{\frac {1}{2}}{\overline {BL_{c}}}}$ und ${\displaystyle {\frac {1}{2}}{\overline {CL_{a}}}}$ subtrahiert und schließlich zum erhaltenen Rest der halbe Inkreisradius ${\displaystyle {\frac {1}{2}}r}$ addiert.

Weiter geht es mit dem Bestimmen der Mittelpunkte der Malfatti-Kreise. Die Hilfsstrecke ${\displaystyle {\overline {PQ}},}$ sprich ${\displaystyle m,}$ mit dem Zirkel abgreifen und jeweils auf die drei Winkelhalbierenden ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ und ${\displaystyle \omega _{\gamma }}$ ab dem Inkreismittelpunkt ${\displaystyle I}$ übertragen; dies ergibt die Punkte ${\displaystyle D,\;E}$ und ${\displaystyle F.}$ Ab den Punkten ${\displaystyle D}$ und ${\displaystyle E}$ einen Kreisbogen bis auf die Dreieckseite ${\displaystyle c}$ und ab ${\displaystyle F}$ einen Kreisbogen bis auf ${\displaystyle a}$ geschlagen, ergibt die Punkte ${\displaystyle C_{1},\;C_{2}}$ und ${\displaystyle A_{2}.}$ Es folgt das Errichten dreier Lote von den Fußpunkten ${\displaystyle C_{1},\;C_{2}}$ und ${\displaystyle A_{2}}$ auf die betreffenden Winkelhalbierenden ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ und ${\displaystyle \omega _{\gamma };,}$ somit ergeben sich die gesuchten Mittelpunkte ${\displaystyle M_{A},\;M_{B}}$ und ${\displaystyle M_{C}.}$

Um die Berührungspunkte ${\displaystyle B_{2},\;A_{1}}$ und ${\displaystyle B_{1}}$ zu erhalten, sind noch drei Lote von den Mittelpunkten ${\displaystyle M_{A},\;M_{B}}$ und ${\displaystyle M_{C}}$ auf die Dreieckseiten ${\displaystyle b,\;a}$ und nochmals ${\displaystyle b}$ zu fällen. Abschließend die Malfatti-Kreise ${\displaystyle k_{A},\;k_{B}}$ und ${\displaystyle k_{C}}$ mit den Radien ${\displaystyle r_{A},\;r_{B}}$ und ${\displaystyle r_{C}}$ einzeichnen und man erhält deren letzten drei Berührungspunkte ${\displaystyle G,\;H}$ und ${\displaystyle J.}$

Somit sind die drei Malfatti-Kreise ${\displaystyle k_{A},\;k_{B}}$ und ${\displaystyle k_{C}}$ mit ihren neun möglichen Berührungspunkten ${\displaystyle C_{1},\;C_{2},\;A_{1},\;A_{2},\;B_{1},\;B_{2},\;G,\;H}$ und ${\displaystyle J}$ konstruiert.

Konstruktion nach Steiner-Petersen

Jakob Steiner brachte 1826 die Malfatti-Kreise in Verbindung mit den Inkreisen aus drei Teildreiecken, die deswegen als Konstruktionselement für die Malfatti-Kreise verwendet werden können. Steiner formulierte dazu den Satz:

Hierbei ist zu betonen, dass die von Steiner erwähnten Tangenten an die Malfatti-Kreise im Allgemeinen nicht die Winkelhalbierenden von ${\displaystyle \triangle ABC}$ sind, sondern deren Spiegelbilder an den Verbindungsgeraden zweier Inkreismittelpunkte der Teildreiecke.

Julius Petersen fand im Jahr 1879 eine elementargeometrische Lösung (Variante ohne vorherige Berechnungen)^[19] des Konstruktionsproblems von Malfatti, die im Folgenden dargestellt ist.^[20]

Konstruktionsbeschreibung

Es ist wegen einer besseren Übersichtlichkeit vorteilhaft, die Konstruktion in drei Hauptschritten, (1)–(3), darzustellen. Dabei werden nur die relevanten Konstruktionselemente vom ersten in den zweiten bzw. vom zweiten in den dritten Hauptschritt übernommen.

(1) Konstruktion der drei Inkreise der Teildreiecke ${\displaystyle \triangle BCI,\;\triangle CAI}$ und ${\displaystyle \triangle ABI.}$^[20]

Nach dem Zeichnen eines z. B. ungleichseitigen Dreiecks ${\displaystyle ABC}$ mit den Seitenlängen ${\displaystyle a,\;b}$ und ${\displaystyle c}$ wird der Mittelpunkt des Inkreises ${\displaystyle I}$ mithilfe der drei Winkelhalbierenden ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ und ${\displaystyle \omega _{\gamma }}$ bestimmt. Die Inkreismittelpunkte ${\displaystyle M_{P},\;M_{Q}}$ und ${\displaystyle M_{R}}$ der Teildreiecke ${\displaystyle \triangle BCI,\;\triangle CAI}$ und ${\displaystyle \triangle ABI}$ erhält man wieder als Schnittpunkt zweier Winkelhalbierenden, z. B. durch Vierteln der Winkel ${\displaystyle \alpha ,\;\beta ,}$ und ${\displaystyle \gamma .}$ Es folgt das Fällen des Lots von ${\displaystyle M_{P}}$ auf die Strecke ${\displaystyle {\overline {BC}}}$ mit dem Fußpunkt ${\displaystyle P}$ und das Ziehen des Inkreises ${\displaystyle k_{P}}$ um ${\displaystyle M_{P}}$ mit dem Radius ${\displaystyle {\overline {M_{P}P}}.}$ Das Fällen der Lote von ${\displaystyle M_{Q}}$ auf ${\displaystyle {\overline {AC}}}$ mit dem Fußpunkt ${\displaystyle Q}$ sowie von ${\displaystyle M_{R}}$ auf ${\displaystyle {\overline {AB}}}$ mit dem Fußpunkt ${\displaystyle R}$ und das Einzeichnen der letzten beiden Inkreise ${\displaystyle k_{Q}}$ und ${\displaystyle k_{R},}$ um ihre Mittelpunkte ${\displaystyle M_{Q}}$ bzw. ${\displaystyle M_{R},}$ schließen sich an.

(2) Konstruktion der drei Tangenten ${\displaystyle {\overline {RZ}},{\overline {PX}}}$ und ${\displaystyle {\overline {QY}}}$

Es geht weiter mit dem Verbinden der Punkte ${\displaystyle R}$ mit ${\displaystyle M_{P},}$ der Halbierung der Strecke ${\displaystyle {\overline {RM_{P}}}}$ in ${\displaystyle M_{1}}$ und dem Einzeichnen des Thaleskreises ${\displaystyle k_{1}.}$ Er schneidet den Inkreis ${\displaystyle k_{P}}$ in den Punkten ${\displaystyle K}$ und ${\displaystyle L.}$ Nun zieht man die erste Tangente vom Punkt ${\displaystyle R}$ durch den Berührungspunkt ${\displaystyle L}$ des Inkreises ${\displaystyle k_{P},}$ bis sie die Dreieckseite ${\displaystyle b}$ in ${\displaystyle Z}$ schneidet.

Im Anschluss daran wird ${\displaystyle P}$ mit ${\displaystyle M_{Q}}$ verbunden, die Strecke ${\displaystyle {\overline {PM_{Q}}}}$ in ${\displaystyle M_{2}}$ halbiert und der Thaleskreis ${\displaystyle k_{2}}$ eingezeichnet. Er schneidet den Inkreis ${\displaystyle k_{Q}}$ in den Punkten ${\displaystyle O}$ und ${\displaystyle N.}$ Das Einzeichnen der zweiten Tangente vom Punkt ${\displaystyle P}$ durch ${\displaystyle N,}$ bis sie die Dreieckseite ${\displaystyle b}$ in ${\displaystyle X}$ schneidet, liefert den Schnittpunkt ${\displaystyle T.}$ Da ${\displaystyle T}$ auch ein Punkt auf der dritten Tangente sein muss, bedarf es zu deren Bestimmung nur noch einer Linie von ${\displaystyle Q}$ durch ${\displaystyle T}$ bis auf die Dreieckseite ${\displaystyle c}$ und den Schnittpunkt ${\displaystyle Y.}$ Somit ist auch die dritte Tangente ${\displaystyle {\overline {QY}}}$ ermittelt.

(3) Konstruktion der Malfatti-Kreise ${\displaystyle k_{A},\;k_{B}}$ und ${\displaystyle k_{C}}$

Zunächst wird im Dreieck ${\displaystyle ARZ}$ die Winkelhalbierende ${\displaystyle \omega _{\epsilon }}$ vom Punkt ${\displaystyle R}$ bis auf die Winkelhalbierende ${\displaystyle \omega _{\alpha }}$ eingezeichnet; dabei ergibt sich der Mittelpunkt ${\displaystyle M_{A}}$ des ersten Malfatti-Kreises. Es folgt das Fällen des Lots von ${\displaystyle M_{A}}$ auf die Strecke ${\displaystyle {\overline {AB}}}$ mit dem Fußpunkt ${\displaystyle C_{1}}$ und das Ziehen des ersten Malfatti-Kreises ${\displaystyle k_{A}}$ um ${\displaystyle M_{A}}$ mit dem Radius ${\displaystyle {\overline {M_{A}C_{1}}}.}$ Das Fällen der Lote von ${\displaystyle M_{A}}$ auf ${\displaystyle {\overline {AC}}}$ mit dem Fußpunkt ${\displaystyle B_{2}}$ sowie von ${\displaystyle M_{A}}$ auf die Tangente ${\displaystyle RZ}$ mit dem Fußpunkt ${\displaystyle C'}$ schließt sich an. Die darauf folgende Linie ab ${\displaystyle M_{A}}$ durch ${\displaystyle C'}$ bis auf die Winkelhalbierende ${\displaystyle \omega _{\beta }}$ erzeugt den Mittelpunkt ${\displaystyle M_{B}.}$ Nach dem Einzeichnen des zweiten Malfatti-Kreises ${\displaystyle k_{B}}$ um ${\displaystyle M_{B}}$ mit dem Radius ${\displaystyle {\overline {M_{B}C'}}}$ werden die Lote von ${\displaystyle M_{B}}$ auf ${\displaystyle {\overline {AB}}}$ mit dem Fußpunkt ${\displaystyle C_{2},}$ von ${\displaystyle M_{B}}$ auf ${\displaystyle {\overline {BC}}}$ mit dem Fußpunkt ${\displaystyle A_{1}}$ sowie von ${\displaystyle M_{B}}$ auf die Tangente ${\displaystyle PX}$ mit dem Fußpunkt ${\displaystyle A'}$ gefällt. Die darauf folgende Linie ab ${\displaystyle M_{B}}$ durch ${\displaystyle A'}$ bis auf die Winkelhalbierende ${\displaystyle \omega _{\gamma }}$ erzeugt den Mittelpunkt ${\displaystyle M_{C}.}$ Nun folgt das Einzeichnen des dritten Malfatti-Kreises ${\displaystyle k_{C}}$ um ${\displaystyle M_{C}}$ mit dem Radius ${\displaystyle {\overline {M_{C}A'}}.}$

Um die Berührungspunkte ${\displaystyle A_{2},\;B_{1}}$ und ${\displaystyle B'}$ zu erhalten, bedarf es noch zweier gefällter Lote vom Mittelpunkt ${\displaystyle M_{C}}$ auf ${\displaystyle {\overline {BC}},}$ von ${\displaystyle M_{C}}$ auf ${\displaystyle {\overline {AC}}}$ und der Verbindung des Punktes ${\displaystyle M_{A}}$ mit ${\displaystyle M_{C}.}$

Somit sind die drei Malfatti-Kreise ${\displaystyle k_{A},\;k_{B}}$ und ${\displaystyle k_{C}}$ mit ihren neun möglichen Berührungspunkten ${\displaystyle C_{1},\;C_{2},\;A_{1},\;A_{2},\;B_{1},\;B_{2},\;A',\;B'}$ und ${\displaystyle C'}$ konstruiert.

Konstruktion nach Lob und Richmond

H. Lob und H. W. Richmond veröffentlichten 1930^[15] eine Lösung für das Maximierungs-Problem von Malfatti. Darin wird der Inkreis des gleichseitigen Dreiecks als ein Kreis von dreien genutzt. Die Bedeckung der Dreiecksfläche durch diese Anordnung der Kreise ist nur marginal größer, nämlich um ${\displaystyle \approx 1\,\%}$, aber dafür ist die Aufgabe leicht und mit wenig Aufwand darstellbar.

Sie haben damit bewiesen,

Konstruktionsbeschreibung

Nach dem Zeichnen eines gleichseitigen Dreiecks ${\displaystyle ABC}$ mit den gleich langen Seitenlängen ${\displaystyle a,\;b}$ und ${\displaystyle c}$ wird der Mittelpunkt des Inkreises ${\displaystyle I}$ mithilfe der drei Winkelhalbierenden ${\displaystyle \omega _{\alpha },\omega _{\beta }}$ und ${\displaystyle \omega _{\gamma }}$ bestimmt. Es folgt das Fällen des Lots von ${\displaystyle I}$ auf die Strecke ${\displaystyle {\overline {BC}}}$ mit dem Fußpunkt ${\displaystyle D}$ und das Ziehen des Inkreises ${\displaystyle k}$ um ${\displaystyle I}$ mit dem Radius ${\displaystyle {\overline {ID}};}$ die Schnittpunkte sind ${\displaystyle E}$ mit der Winkelhalbierenden ${\displaystyle \omega _{\alpha }}$ und ${\displaystyle F}$ mit der Winkelhalbierenden ${\displaystyle \omega _{\beta }.}$ Das Fällen der Lote von ${\displaystyle I}$ auf ${\displaystyle {\overline {AC}}}$ mit dem Fußpunkt ${\displaystyle G}$ sowie von ${\displaystyle I}$ auf ${\displaystyle {\overline {AB}}}$ mit dem Fußpunkt ${\displaystyle H}$ schließt sich an.

Für die kleineren Kreise zieht man (im gleichseitigen Dreieck) zwei Parallelen zur Strecke ${\displaystyle {\overline {AB}}}$ – eine ab dem Punkt ${\displaystyle E}$ bis auf die Strecke ${\displaystyle {\overline {AC}}}$ mit dem Schnittpunkt ${\displaystyle J}$, die zweite ab dem Punkt ${\displaystyle F}$ bis auf die Strecke ${\displaystyle {\overline {BC}}}$ mit dem Schnittpunkt ${\displaystyle K.}$ Das Errichten des Lots mit dem Fußpunkt ${\displaystyle J}$ auf die Winkelhalbierende ${\displaystyle \omega _{\alpha }}$ und das Errichten des Lots auf die Winkelhalbierende ${\displaystyle \omega _{\beta }}$ mit dem Fußpunkt ${\displaystyle K}$ ergibt die Mittelpunkte ${\displaystyle M_{A}}$ und ${\displaystyle M_{B}.}$ Nun wird ein Kreis um ${\displaystyle M_{A}}$ mit dem Radius ${\displaystyle {\overline {M_{A}E}}}$ und ein Kreis um ${\displaystyle M_{B}}$ mit dem Radius ${\displaystyle {\overline {M_{B}F}}}$ gezogen. Um die beiden letzten Berührungspunkte zu erhalten, werden abschließend zwei Lote auf ${\displaystyle {\overline {AB}}}$ gefällt, von ${\displaystyle M_{A}}$ und von ${\displaystyle M_{B}}$, dabei ergeben sich die Fußpunkte ${\displaystyle L}$ und ${\displaystyle M.}$

Somit sind in das gleichseitige Dreieck die drei Kreise ${\displaystyle k,\;k_{A}}$ und ${\displaystyle k_{B}}$ mit ihren neun möglichen Berührungspunkten ${\displaystyle D,\;E,\;F,\;G,\;H,\;J,\;K,\;L}$ und ${\displaystyle M}$ konstruiert.

Konstruktion nach Goldberg

Michael Goldberg veröffentlichte 1967 einen Aufsatz, in dem er zeigte, dass Malfattis Konstruktion, unabhängig von der Form des Dreiecks, in keinem Fall das Maximierungs-Problem erfüllen kann. Zu diesem Ergebnis kam er – ohne es zu beweisen –^[8] durch Untersuchungen anhand unterschiedlicher Formen der Dreiecke, die alle eines gemeinsam hatten: Einer der drei Kreise war stets der Inkreis.^[16]

Konstruktionsbeschreibung

Nach dem Zeichnen des unregelmäßigen Dreiecks ${\displaystyle ABC}$ wird der Mittelpunkt ${\displaystyle I}$ des Inkreises ${\displaystyle k_{1}}$ mithilfe der zwei Winkelhalbierenden ${\displaystyle \omega _{\alpha }}$ und ${\displaystyle \omega _{\gamma }}$ bestimmt. Damit ergeben sich die Strecken ${\displaystyle {\overline {AI}}}$ und ${\displaystyle {\overline {CI}}.}$ Es folgt das Fällen des Lots von ${\displaystyle I}$ auf die Strecke ${\displaystyle {\overline {AB}}}$ mit dem Fußpunkt ${\displaystyle D}$ und das Ziehen des Inkreises ${\displaystyle k_{1}}$ um ${\displaystyle I}$ mit dem Radius ${\displaystyle {\overline {ID}};}$ der Schnittpunkt auf ${\displaystyle \omega _{\alpha }}$ ist ${\displaystyle E.}$ Das Fällen der Lote von ${\displaystyle I}$ auf ${\displaystyle {\overline {AC}}}$ mit dem Fußpunkt ${\displaystyle F}$ sowie von ${\displaystyle I}$ auf ${\displaystyle {\overline {BC}}}$ mit dem Fußpunkt ${\displaystyle G}$ schließt sich an.

Der Mittelpunkt des zweiten Kreises ${\displaystyle k_{2}}$ wird nun sehr einfach mit zwei Schritten bestimmt. Es bedarf dafür nur einer Senkrechten zur Strecke ${\displaystyle {\overline {AI}}}$ ab dem Punkt ${\displaystyle E,}$ die ${\displaystyle {\overline {AC}}}$ in ${\displaystyle H}$ schneidet, und einer Winkelhalbierenden des Winkels ${\displaystyle AHE.}$ Der damit erzeugte Punkt ${\displaystyle J}$ ist der Mittelpunkt des zweiten Kreises ${\displaystyle k_{2}}$ mit dem Radius ${\displaystyle {\overline {JE}}}$ und den Berührungspunkten ${\displaystyle K}$ und ${\displaystyle L}$ mit zwei Seiten des Dreiecks.

Um für den dritten und letzten gesuchten Kreis den größtmöglichen Radius zu finden, werden zuerst auf zwei Winkelhalbierenden – auf dreien, falls es die Form des Dreiecks verlangt – mögliche Radien bestimmt. Man erhält sie durch analoge Wiederholung der Konstruktionsschritte des zweiten Kreises ${\displaystyle k_{2}}$ mit Mittelpunkt ${\displaystyle J.}$ Die gepunkteten Linien im nebenstehenden Bild zeigen den auf der Winkelhalbierenden ${\displaystyle \omega _{\beta }}$ konstruierten Radius ${\displaystyle {\overline {SR}},}$ als Vergleichsmöglichkeit zum Radius ${\displaystyle {\overline {OM}}}$ auf ${\displaystyle \omega _{\alpha }.}$ Die Bewertung der beiden Radien ergibt ${\displaystyle {\overline {SR}}<{\overline {OM}}}$. Daraus folgt: Der Kreis um den Mittelpunkt ${\displaystyle O}$ ist der gesuchte größtmögliche dritte Kreis ${\displaystyle k_{3}}$.

Somit sind in das unregelmäßige Dreieck die drei Kreise ${\displaystyle k_{1},\;k_{2}}$ und ${\displaystyle k_{3}}$ mit ihren neun möglichen Berührungspunkten ${\displaystyle D,\;E,\;F,\;G,\;K,\;L,\;M,\;P}$ und ${\displaystyle Q}$ konstruiert.

Konstruktion nach Salgaller und Los

W. A. Salgaller^[21] und G. A. Los^[7] veröffentlichten – nach ihrer Lösung 1992 (siehe Geschichtliches) – 1994 im Journal of Mathematical Sciences ihre Lösung des Malfatti’schen Maximierungs-Problems.^[22][23] Darin sind u. a. fünf allgemeine Dreiecke zu sehen, in denen jeweils der Inkreis einer der drei sich nicht überlappenden Kreise ist. Nur in einem Dreieck davon, in Konstruktion nach Goldberg beschrieben, liegen diese drei Kreise auf derselben Winkelhalbierenden.^[24]

Bedeckung der Dreiecksfläche durch drei Kreise

• Die Methode nach Malfatti (Bild 1) sowie die Methode nach Steiner-Petersen erreicht

${\displaystyle \left({\sqrt {3}}-{\frac {3}{2}}\right)\cdot \pi \approx 0{,}72910}$ oder ca. ${\displaystyle 72{,}91\,\%.}$^[4]

• Die Methode nach Lob und Richmond (Bild 2) erreicht

${\displaystyle {\frac {11{\sqrt {3}}}{81}}\cdot \pi \approx 0{,}73895}$ oder ca. ${\displaystyle 73{,}90\,\%.}$^[5]

• Methode mit Inkreis nach Salgaller und Los^[7] sowie die Methode nach Goldberg (Bild 3 und Bild 4):

Die Bedeckung der Dreiecksfläche, z. B. als prozentualer Wert, ist von der gewählten Form des Ausgangsdreiecks sowie von der Position der Kreise ${\displaystyle k_{2}}$ und ${\displaystyle k_{3}}$ abhängig. Für die dargestellte Formen, mit ${\displaystyle A}$ für die entsprechenden Flächeninhalte, gilt die Prozentformel:

${\displaystyle {\frac {A_{k_{1}}+A_{k_{2}}+A_{k_{3}}}{A{_{\triangle {ABC}}}}}\cdot 100\,\%,}$

dies ergibt eine Bedeckung der Dreiecksfläche für das Dreieck in Bild 3 von ${\displaystyle \approx 72{,}70\;\%}$ bzw. für das Dreieck in Bild 4 von ${\displaystyle \approx 76{,}1\;\%.}$

• 
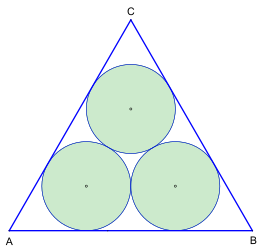  Bild 1: Methode nach Malfatti sowie die Methode nach Steiner-Petersen im gleichseitigen Dreieck, Bedeckung der Dreiecksfläche ca. 72,91 %
• 
  Bild 2: Methode nach Lob und Richmond im gleichseitigen Dreieck, Bedeckung der Dreiecksfläche ca. 73,90 %
• 
  Bild 3: Methode nach Salgaller und Los sowie die Methode nach Goldberg mit Inkreis ${\displaystyle k_{1}}$; in der dargestellten Form ist die Bedeckung der Dreiecksfläche ca. 72,70 %
• 
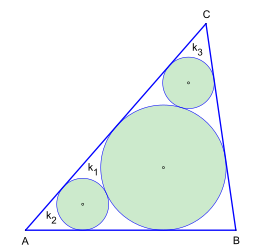  Bild 4: Methode nach Salgaller und Los sowie die Methode nach Goldberg mit Inkreis ${\displaystyle k_{1}}$; in der dargestellten Form ist die Bedeckung der Dreiecksfläche ca. 76,1 %

Literatur

• Kurt Loeber: Beiträge zur Lösung und Geschichte des Malfattischen Problems und seiner Erweiterungen. Inaugural-Dissertation. SUB Göttingen, Göttinger Digitalisierungszentrum, 1914, abgerufen am 4. Oktober 2020. 
• Marco Andreatta, Andras Bezdek, Jan P. Boronski: The Malfatti Problem: two centuries of debate. Mathematical Intelligencer, 2011, Nr. 1.
• Heinrich Dörrie: Malfatti’s Problem in 100 Great Problems of Elementary Mathematics: Their History and Solutions. Dover, New York 1965, ISBN 0-486-61348-8, S. 147–151.
• Michael Goldberg: On the Original Malfatti Problem (PDF; 553 kB) In Math. Mag. Nr. 40, 1967, S. 241–247.
• Charles Stanley Ogilvy: Excursions in Geometry. Dover, New York 1990, ISBN 0-486-26530-7.
• W. A. Salgaller, G. A. Los: The solution of Malfatti’s problem. In: Journal of Mathematical Sciences. Band 72, Nr. 4, 1994, S. 3163–3177. 
• Carl Adams: Das Malfattische Problem. Neu gelöst. Steiner, Winterthur 1846 (Digitalisat). 

Weblinks

• Eric W. Weisstein: Malfatti Circles. In: MathWorld (englisch).
• Eric W. Weisstein: Malfatti’s Problem. In: MathWorld (englisch).
• Malfatti’s Problem. In: Cut The Knot. Abgerufen am 4. Oktober 2020 (englisch). 

Einzelnachweise

1. ↑ Kurt Loeber: Geschichtlicher Überblick (Einleitung). In: Beiträge zur Lösung und Geschichte des Malfattischen Problems und seiner Erweiterungen. SUB Göttingen, Götinger Digitalisierungszentrum, 1914, S. 1, abgerufen am 15. November 2020. 
2. ↑ Gianfrancesco Malfatti: Memoria sopra un problema stereotomica. (PDF; 966 kB) Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, S. 235–244, abgerufen am 15. November 2020.
3. ↑ Gianfrancesco Malfatti: Memoria sopra un problema stereotomica. (PDF; 966 kB) Memorie di Matematica e Fisica della Società Italiana delle Scienze, No. 10, 1, 1803, S. 243 ff, abgerufen am 15. November 2020.
4. ↑ ^{a b} Ingmar Lehmann: 1. Die Malfatti-Story Seite 1. (PDF) In: Das Malfatti-Problem – Ein Thema in der Begabtenförderung. TU Dortmund, 2003, abgerufen am 19. November 2020. 
5. ↑ ^{a b c d} Ingmar Lehmann: 1. Die Malfatti-Story Seite 2. (PDF) In: Das Malfatti-Problem – Ein Thema in der Begabtenförderung. TU Dortmund, 2003, abgerufen am 7. November 2020. 
6. ↑ ^{a b c d} Raúl Ibáñez: El problema de Malfatti. culturacientifica, Matemoción, 5. April 2017, abgerufen am 5. Oktober 2018 (spanisch). 
7. ↑ ^{a b c} Sic! – Diese Schreibweise Los weicht gemäß den Transkriptionsregeln der deutschsprachigen Wikipedia (Fußnote 6) von der anderswo großteils zu findenden Schreibweise Los’ (mit Apostroph) ab, siehe dazu z. B. auch hier.
8. ↑ ^{a b c d} Ingmar Lehmann: Konstruktion der Malfatti-Kreise, S. 3–5. (PDF; 143 kB) In: Das Malfatti-Problem – Ein Thema in der Begabtenförderung, 15 Seiten. TU Dortmund, 2003, abgerufen am 4. Oktober 2020. 
9. ↑ ^{a b} Kurt Loeber: Geschichtlicher Überblick (Einleitung). In: Beiträge zur Lösung und Geschichte des Malfattischen Problems und seiner Erweiterungen. SUB Göttingen, Götinger Digitalisierungszentrum, 1914, S. 2 ff., abgerufen am 4. Oktober 2020. 
10. ↑ Jacques Bernoulli: Oeuvres complètes, Genf 1744, Band 1, S. 303.
11. ↑ Jakob Steiner: Einige geometrische Sätze; Jacob Steiner’s Gesammelte Werke, Band 1, G. Reimer, 1881, S. 3, in der Google-Buchsuche, abgerufen am 15. November 2020.
12. ↑ Jakob Steiner: Einige geometrische Betrachtungen; Jacob Steiner’s Gesammelte Werke, Band 1, G. Reimer, 1881, S. 19, in der Google-Buchsuche, abgerufen am 15. November 2020.
13. ↑ Alfred Clebsch: Anwendung der elliptischen Funktionen auf ein Problem der Geometrie des Raumes. In: Journal für Reine und Angewandte Mathematik (Crelle’s Journal), Band 53. SUB Göttingen, Götinger Digitalisierungszentrum, 1857, S. 292–308, abgerufen am 15. November 2020. 
14. ↑ Ajima Naonobu in seinem Hauptwerk Fukyo sampo von 1799. John J. O’Connor, Edmund F. Robertson: Malfatti-Kreis. In: MacTutor History of Mathematics archive (englisch).
15. ↑ ^{a b} H. Lob, H. W. Richmond: On the Solutions of Malfatti’s Problem for a Triangle. (PDF) London Mathematical Society, 1930, abgerufen am 20. November 2020. 
16. ↑ ^{a b} Michael Goldberg: On the Original Malfatti Problem. In: Florida Atlantic University (Hrsg.): Mathematics Magazine. Band 40, Nr. 5, November 1967, S. 241–247, JSTOR:2688277 (On the Original Malfatti Problem [PDF; abgerufen am 20. November 2020]). 
17. ↑ Giancarlo Lombardi: Proving the solution of Malfatti’s marble problem. In: Rendiconti del Circolo Matematico di Palermo Series 2. 20. Juni 2022, ISSN 0009-725X, doi:10.1007/s12215-022-00759-2 (springer.com [abgerufen am 20. Juni 2022]). 
18. ↑ Ingmar Lehmann: Konstruktion nach Steiner-Petersen. (PDF) In: Das Malfatti-Problem – Ein Thema in der Begabtenförderung. TU Dortmund, 2003, S. 5, abgerufen am 2. Oktober 2018. 
19. ↑ Julius Petersen, R. von Fischer-Benzon (Übersetzer): Methoden und Theorien zur Auflösung geometrischer Konstruktionsaufgaben. (PDF) In: Konstruktionsaufgabe 404. University of Michigan, Library, 1879, S. 102–104, abgerufen am 15. November 2020. 
20. ↑ ^{a b} Ingmar Lehmann: Konstruktion nach Steiner-Petersen, S. 8 ff. (PDF) In: Das Malfatti-Problem – Ein Thema in der Begabtenförderung. TU Dortmund, 2003, abgerufen am 2. Oktober 2018. 
21. ↑ Sic! – Diese Schreibweise Salgaller entspricht den Wikipedia:Namenskonventionen, siehe hierzu auch Wiktor Abramowitsch Salgaller
22. ↑ W. A. Salgaller, G. A. Los: The solution of Malfatti’s problem. In: Journal of Mathematical Sciences. Band 72, Nr. 4, 1994, S. 3163 ff. (springer.com [abgerufen am 5. Oktober 2020] Fig. 1, Springer Link, PDF). 
23. ↑ Jaime Rangel-Mondragon: The Malfatti Problem. (PDF) In: Wolfram Demonstrations Project. Wolfram, 2011, abgerufen am 24. November 2020. 
24. ↑ Arnold Math Jn: 2.2 Solution to Malfatti’s Marble Problem. (PDF) In: On Malfatti’s Marble Problem. Institute for Mathematical Sciences, Stony Brook University, New York, Juni 2016, abgerufen am 24. November 2020.