Kombinatorische Optimierung

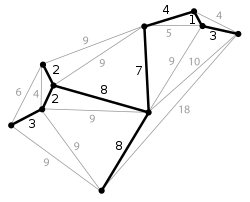
Der minimale Spannbaum eines Graphs. Diesen Spannbaum zu bestimmen ist ein Problem der kombinatorischen Optimierung.

Die kombinatorische Optimierung ist ein Teilgebiet der mathematischen Optimierung, welches sich damit beschäftigt, ein optimales Element in einer endlichen, aber sehr großen, Menge zu bestimmen. Die meisten kombinatorischen Optimierungsprobleme können natürlich in der Sprache der Graphentheorie oder der (gemischt-) ganzzahligen linearen Optimierung dargestellt werden.[1] Typische kombinatorische Optimierungsprobleme sind das Problem des Handlungsreisenden, der minimale Spannbaum und das Rucksackproblem. Die kombinatorische Optimierung ist Teil der diskreten Mathematik und des Operations Research mit engem Bezug zur theoretischen Informatik und der künstlichen Intelligenz.

Informelle Definition

Wie der Name bereits andeutet, geht es in der kombinatorischen Optimierung darum, aus einer großen Menge von diskreten Elementen (Gegenstände, Orte) eine Teilmenge zu konstruieren, die gewissen Nebenbedingungen entspricht und bezüglich einer Zielfunktion (auch Kosten- oder Bewertungsfunktion) optimal ist (kleinstes Gewicht, kürzeste Strecken, …). Derartige Fragestellungen spielen in der Praxis eine große Rolle. Die optimale Wegeplanung eines Bohrers auf einer Leiterplatte[2], die kostenoptimale Belegung von Maschinen[3] oder die möglichst günstige Routenplanung[4] sind allesamt Vertreter dieser Problemklasse.

Formale Definition

Ein kombinatorisches Optimierungsproblem

P : min x f ( x ) s. t. x ∈ M . {\displaystyle P:\qquad \min _{x}f(x)\quad {\text{s. t.}}\quad x\in M.}
besteht aus einer diskreten, d. h. endlichen oder abzählbar unendlichen, Menge aller möglicher Lösungen M {\displaystyle M} , die als zulässige Menge bezeichnet wird und einer Zielfunktion f : M → R {\displaystyle f\colon M\rightarrow \mathbb {R} } darstellt, die jedem Element aus M {\displaystyle M} einen Zielfunktionswert (Kosten, Gewinn, …) zuweist. Ziel ist, eine global optimale Lösung x ⋆ ∈ L {\displaystyle x^{\star }\in L} zu finden, so dass kein x ∈ M {\displaystyle x\in M} mit f ( x ) < f ( x ⋆ ) {\displaystyle f(x)<f(x^{\star })} existiert (bei einem Minimierungsproblem). Es lässt sich in der Regel als (gemischt-)ganzzahliges lineares Optimierungsproblem (ILP oder MILP) darstellen.

Algorithmen und Komplexität

Die Probleme, mit denen man sich in der kombinatorischen Optimierung beschäftigt, sind teilweise effizient, d. h. mit polynomiellem Aufwand, lösbar. Andere Vertreter gehören zur Klasse der NP-schweren Probleme, deren Lösung sich für wachsende Problemgröße in der Regel als sehr aufwändig gestaltet.

Die Algorithmen, die die Lösungen erzeugen sollen, versuchen daher meist, den Suchraum zu beschränken. Vertreter dieser Algorithmen sind beispielsweise Branch-and-Bound bzw. Branch-and-Cut, welche exakte, garantiert optimale Lösungen erzeugen. Dafür wird das Problem als ganzzahliges Optimierungsproblem formuliert, bei dem dann die Belegung von Entscheidungsvariablen darüber entscheidet, ob bestimmte Elemente zur Lösung gehören oder nicht.

Andere Algorithmen nutzen spezielles Wissen über die Problemstruktur, sog. Heuristiken oder Meta-Heuristiken. Hierzu gehört z. B. die lokale Suche mit ihren Ausprägungen Simulierte Abkühlung oder Tabu Search. Diese Verfahren können aber meist nicht garantieren, dass eine global optimale Lösung gefunden werden kann.

Bekannte Probleme

Literatur

  • William J. Cook, William H. Cunningham, William R. Pulleyblank, Alexander Schrijver: Combinatorial Optimization. 1. Auflage. John Wiley & Sons, New York u. a. 1997, ISBN 0-471-55894-X.
  • Pierluigi Crescenzi, Viggo Kann, Magnús Halldórsson, Marek Karpinski, Gerhard Woeginger: A compendium of NP optimization problems.
  • Bernhard Korte, Jens Vygen: Kombinatorische Optimierung: Theorie und Algorithmen. 2. Auflage. Springer Spektrum, Berlin 2012, ISBN 978-3-642-25400-0.
  • Christos H. Papadimitriou, Kenneth Steiglitz: Combinatorial Optimization: Algorithms and Complexity. Dover Publications, Mineola, New York 1998, ISBN 0-486-40258-4.
  • Eugene Lawler: Combinatorial Optimization: Networks and Matroids, Oxford University Press 1995 (zuerst 1976)
  • Alexander Schrijver: Combinatorial optimization – polyhedra and efficiency, 3 Bände, Springer, Berlin / Heidelberg / New York 2003.

Einzelnachweise

  1. ↑ Bernhard Korte, Jens Vygen: Combinatorial optimization: theory and algorithms (= Algorithms and combinatorics). 5. Auflage. Springer, Berlin Heidelberg 2012, ISBN 978-3-642-24487-2 (uni-muenchen.de [PDF; abgerufen am 12. Januar 2024]). 
  2. ↑ William Cook: VLSI Application: An Optimal 85,900-Point Tour. In: https://www.math.uwaterloo.ca/. Abgerufen am 13. Januar 2024. 
  3. ↑ Xiaoyan Zhu, Wilbert E. Wilhelm: Scheduling and lot sizing with sequence-dependent setup: A literature review. In: IIE Transactions. Band 38, Nr. 11, November 2006, ISSN 0740-817X, S. 987–1007, doi:10.1080/07408170600559706. 
  4. ↑ Jan Dethloff: Vehicle routing and reverse logistics: The vehicle routing problem with simultaneous delivery and pick-up. In: OR Spektrum. Band 23, Nr. 1, Februar 2001, ISSN 0171-6468, S. 79–96, doi:10.1007/pl00013346 (academia.edu [PDF; abgerufen am 12. Januar 2024]).