Fünfeck

Ein Fünfeck, auch Pentagon (von altgriechisch πεντάγωνον pentágōnon „Fünfeck“), ist eine geometrische Figur. Es gehört zur Gruppe der Vielecke (Polygone) und ist durch fünf Punkte definiert. Sind alle fünf Seiten gleich lang, spricht man von einem gleichseitigen Fünfeck. Sind darüber hinaus alle Winkel an den fünf Ecken gleich groß, dann wird das Fünfeck regulär oder regelmäßig genannt.

Einteilung

Fünfecke können, wie alle Polygone, welche keine Dreiecke sind, unterteilt werden in:

• überschlagenes Fünfeck: Mindestens zwei Seiten schneiden einander.
• konkaves Fünfeck: Mindestens ein Innenwinkel ist größer als 180°. Ein Fünfeck kann maximal zwei derartige Winkel haben.
• konvexes Fünfeck: Alle Innenwinkel sind kleiner als 180°.
• Sehnenfünfeck: Alle Ecken liegen auf einem gemeinsamen Umkreis.
• regelmäßiges Fünfeck: Alle Seiten sind gleich lang und alle Innenwinkel gleich groß. Regelmäßige Fünfecke können konvex oder überschlagen sein.
• regelmäßiges überschlagenes Fünfeck: Es ergibt sich, wenn beim Verbinden der fünf Eckpunkte jedes Mal einer ${\displaystyle \left\{5/2\right\}}$ oder zwei ${\displaystyle \left\{5/3\right\}}$ übersprungen werden und die somit erzeugten Sehnen gleich lang sind. Notiert werden solche regelmäßigen Sterne mit Schläfli-Symbolen ${\displaystyle \left\{n/k\right\}}$, wobei ${\displaystyle n}$ die Anzahl der Eckpunkte angibt und jeder ${\displaystyle k}$-te Punkt verbunden wird.

Es gibt nur einen regelmäßigen Fünfstrahlstern, das Pentagramm. Da es mit einem geschlossenen Polygonzug gezeichnet werden kann, ist es auch ein sogenanntes Sternpolygon mit dem Schläfli-Symbol ${\displaystyle \left\{5/2\right\},\;\left\{5/3\right\}}$.

• Regelmäßiger Fünfstrahlstern Pentagramm
• 
  Sternpolygon ${\displaystyle \left\{5/2\right\},\;\left\{5/3\right\}}$

Allgemeines Fünfeck

Winkel

Die Summe der Innenwinkel eines regelmäßigen Fünfecks beträgt 540°, also 3 mal 180°, und ergibt sich aus einer allgemeinen Formel für Polygone, in der für die Variable ${\displaystyle n}$ die Anzahl der Eckpunkte des Polygons eingesetzt werden muss (in diesem Fall ${\displaystyle n=5}$):

${\displaystyle \sum \alpha =(n-2)\cdot 180^{\circ }=3\cdot 180^{\circ }=540^{\circ }}$

Fläche

Ein ebenes Fünfeck besitzt einen eindeutig bestimmbaren Flächeninhalt, welcher sich stets durch Zerlegen in Dreiecke berechnen lässt.

Regelmäßiges Fünfeck

Formeln

Mathematische Formeln zum regelmäßigen Fünfeck
Innenwinkel	${\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}$ ${\displaystyle \alpha =\arccos \left({\frac {1-{\sqrt {5}}}{4}}\right)=108^{\circ }}$
Zentriwinkel	${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{5}}=72^{\circ }}$ ${\displaystyle \mu =\arccos \left({\frac {{\sqrt {5}}-1}{4}}\right)=72^{\circ }}$
Flächeninhalt	${\displaystyle A={\frac {a^{2}}{4}}\cdot {\sqrt {25+10\cdot {\sqrt {5}}}}\approx 1{,}720\cdot a^{2}}$
Höhe	${\displaystyle h=r_{u}+r_{i}={\frac {a}{2}}\cdot {\sqrt {5+2\cdot {\sqrt {5}}}}\approx 1{,}539\cdot a}$
Seitenlänge	${\displaystyle a=2\cdot r_{u}\cdot \sin \left(36^{\circ }\right)}$ ${\displaystyle a=r_{u}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}176\cdot r_{u}}$
Länge der Diagonalen	${\displaystyle d=2\cdot a\cdot \sin \left(54^{\circ }\right)}$ ${\displaystyle d=a\cdot {\frac {1}{2}}\cdot (1+{\sqrt {5}})\approx 1{,}618\cdot a}$
Umkreisradius	${\displaystyle r_{u}={\frac {a}{2\cdot \sin(36^{\circ })}}}$ ${\displaystyle r_{u}=a\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\approx 0{,}851\cdot a}$
Inkreisradius	${\displaystyle r_{i}=a\cdot {\frac {1}{2}}\cdot \cot \left(36^{\circ }\right)}$ ${\displaystyle r_{i}=a\cdot {\frac {1}{2}}\cdot {\sqrt {1+{\frac {2}{\sqrt {5}}}}}\approx 0{,}688\cdot a}$

Innenwinkel

Der Winkel, den zwei benachbarte Seiten im ebenen, regelmäßigen Fünfeck miteinander einschließen, beträgt (wiederum nach einer allgemeinen Formel für regelmäßige Polygone):

${\displaystyle \alpha ={\frac {(n-2)}{n}}\cdot 180^{\circ }={\frac {3}{5}}\cdot 180^{\circ }=108^{\circ }}$

oder auch

${\displaystyle \alpha =\arccos \left({\frac {1-{\sqrt {5}}}{4}}\right)=108^{\circ }}$

Zentriwinkel

Der Zentriwinkel oder Mittelpunktswinkel ${\displaystyle \mu }$ wird von zwei benachbarten Umkreisradien ${\displaystyle r_{u}}$ eingeschlossen. In der allgemeinen Formel ist für die Variable ${\displaystyle n}$ die Zahl ${\displaystyle 5}$ einzusetzen.

${\displaystyle \mu ={\frac {360^{\circ }}{n}}={\frac {360^{\circ }}{5}}=72^{\circ }}$

oder auch

${\displaystyle \mu =\arccos \left({\frac {{\sqrt {5}}-1}{4}}\right)=72^{\circ }}$

Flächeninhalt

Der Flächeninhalt A eines regelmäßigen Fünfecks der Seitenlänge ${\displaystyle a}$ ist das Fünffache des Flächeninhalts eines von seinem Mittelpunkt und zwei seiner Eckpunkte aufgespannten Dreiecks.

${\displaystyle A=5\cdot {\frac {1}{2}}\cdot a\cdot \tan 54^{\circ }\cdot {\frac {a}{2}}={\frac {5}{4}}\cdot a^{2}\cdot \tan 54^{\circ }\approx 1{,}720\cdot a^{2}}$

Allgemein mit dem Umkreisradius r_u

${\displaystyle A={\frac {5}{8}}\cdot r_{u}^{2}\cdot {\sqrt {10+2\cdot {\sqrt {5}}}}}$

oder auch

${\displaystyle A={\frac {5}{2}}\cdot r_{u}^{2}\cdot \sin {72^{\circ }}\approx 2{,}378\cdot r_{u}^{2}}$

Seitenlänge und Umkreisradius

Das Fünfeck wird in 5 kongruente Dreiecke zerlegt. Nimmt man die Hälfte eines solchen Dreiecks, also ein rechtwinkliges Dreieck ${\displaystyle AGM}$ mit den Seiten ${\displaystyle {\frac {a}{2}}}$, Umkreisradius ${\displaystyle r_{u}}$ und Inkreisradius ${\displaystyle r_{i}}$ sowie mit dem halben Zentriwinkel ${\displaystyle {\frac {72^{\circ }}{2}}=36^{\circ },}$ so gilt

${\displaystyle \sin(36^{\circ })={\frac {\frac {a}{2}}{r_{u}}}={\frac {a}{2\cdot r_{u}}}}$,

daraus folgt  

${\displaystyle a=2\cdot r_{u}\cdot \sin(36^{\circ })}$.

Löst man nach ${\displaystyle r_{u}}$ auf, so erhält man

${\displaystyle r_{u}={\frac {a}{2\cdot \sin(36^{\circ })}}}$.

Verwendet man für die Sinus-Werte deren Quadratwurzeln, so gilt auch

${\displaystyle a=r_{u}\cdot {\sqrt {\frac {5-{\sqrt {5}}}{2}}}\approx 1{,}176\cdot r_{u}}$.

${\displaystyle r_{u}=a\cdot {\sqrt {\frac {5+{\sqrt {5}}}{10}}}\approx 0{,}851\cdot a}$.

Länge der Diagonalen

Im nebenstehenden Bild ist eine von vier möglichen Diagonalen eingezeichnet. Die Diagonale lässt sich aus dem Hilfsdreieck ${\displaystyle EFD}$ bestimmen. Es ergibt sich

${\displaystyle \sin \left(54^{\circ }\right)={\frac {\frac {d}{2}}{a}}}$,

daraus folgt

${\displaystyle d=2\cdot a\cdot \sin \left(54^{\circ }\right)}$.

Verwendet man die Quadratwurzel des Sinus-Wertes

${\displaystyle \sin \left(54^{\circ }\right)={\frac {1}{4}}\cdot (1+{\sqrt {5}})}$

so gilt auch

${\displaystyle d=2\cdot a\cdot {\frac {1}{4}}\cdot (1+{\sqrt {5}})=a\cdot {\frac {1}{2}}\cdot (1+{\sqrt {5}})\approx 1{,}618\cdot a}$.

Inkreisradius

Auch der Inkreisradius ${\displaystyle r_{i}}$ lässt sich mithilfe eines halbierten Bestimmungsdreiecks, sprich mit dem rechtwinkligen Dreieck ${\displaystyle AGM}$, ermitteln. Es ergibt sich

${\displaystyle \cot \left(36^{\circ }\right)={\frac {r_{i}}{\frac {a}{2}}}}$,

daraus folgt

${\displaystyle r_{i}=a\cdot {\frac {1}{2}}\cdot \cot \left(36^{\circ }\right)}$.

Wegen

${\displaystyle \cot \left(36^{\circ }\right)={\frac {\sqrt {1-\sin ^{2}\left(36^{\circ }\right)}}{\sin \left(36^{\circ }\right)}}}$

und der Quadratwurzel des Sinuswertes

${\displaystyle \sin \left(36^{\circ }\right)={\frac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}}$,

eingesetzt in

${\displaystyle \cot \left(36^{\circ }\right)={\frac {\sqrt {1-\left({\frac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}\right)^{2}}}{\left({\frac {1}{4}}{\sqrt {10-2{\sqrt {5}}}}\right)}}={\sqrt {1+{\frac {2}{\sqrt {5}}}}}}$,

gilt auch

${\displaystyle r_{i}=a\cdot {\frac {1}{2}}\cdot {\sqrt {1+{\frac {2}{\sqrt {5}}}}}\approx 0{,}688\cdot a}$.

Der Goldene Schnitt im Fünfeck

Regelmäßiges Fünfeck und Pentagramm bilden eine Grundfigur, in der das Verhältnis des Goldenen Schnittes wiederholt auftritt. Die Seite des Fünfecks befindet sich im goldenen Verhältnis zu seinen Diagonalen. Die Diagonalen untereinander teilen sich wiederum im goldenen Verhältnis, d. h. AD verhält sich zu BD wie BD zu CD.^[1]

Der Beweis nutzt die Ähnlichkeit gewählter Dreiecke.

Konstruktion mit Zirkel und Lineal bei gegebenem Umkreis

Für das regelmäßige Fünfeck existiert eine mathematisch exakte Konstruktion zur Bestimmung der Seitenlänge (siehe Abbildung).

1. Zeichne einen Kreis (späterer Umkreis, blau) mit Radius r um den Mittelpunkt M.
2. Zeichne zwei zueinander senkrechte Durchmesser (rot) ein.
3. Halbiere einen Radius (magenta, Punkt D).
4. Zeichne einen Kreis (grün) mit dem Radius DE um Punkt D. Er schneidet die Gerade AM im Punkt F. Die Strecke EF ist die Länge der Seite.
5. Zum Abtragen auf dem Umkreis einen weiteren Kreisbogen (orange) mit Radius EF um E zeichnen. Er schneidet den ersten Kreis (blau) in G. Vorgang entsprechend wiederholen.

Berechnung zur Konstruktion:

${\displaystyle {\overline {EM}}=r\cdot 1}$

${\displaystyle {\overline {DM}}=r\cdot {\frac {1}{2}}}$

${\displaystyle {\overline {DE}}=r\cdot {\sqrt {1+\left({\frac {1}{2}}\right)^{2}}}=r\cdot {\frac {\sqrt {5}}{2}}}$

${\displaystyle {\overline {MF}}=r\cdot \left({\frac {\sqrt {5}}{2}}-{\frac {1}{2}}\right)=r\cdot {\frac {{\sqrt {5}}-1}{2}}}$

${\displaystyle {\overline {EF}}=r\cdot {\sqrt {1+\left({\frac {{\sqrt {5}}-1}{2}}\right)^{2}}}}$

Umformen des Faktors:

${\displaystyle {\frac {\overline {EF}}{r}}={\sqrt {1+{\frac {5-2\cdot {\sqrt {5}}+1}{4}}}}={\sqrt {{\frac {4}{4}}+{\frac {5-2\cdot {\sqrt {5}}+1}{4}}}}}$

${\displaystyle {\frac {\overline {EF}}{r}}={\sqrt {\frac {4+5-2\cdot {\sqrt {5}}+1}{4}}}={\sqrt {\frac {10-2\cdot {\sqrt {5}}}{4}}}}$

${\displaystyle {\frac {\overline {EF}}{r}}={\sqrt {\frac {5-{\sqrt {5}}}{2}}}}$

Das entspricht genau dem Faktor in der obigen Formel für die Seitenlänge.

Die Seiten des nicht eingezeichneten Dreiecks MFE entsprechen exakt den Seitenlängen des regelmäßigen Sechsecks (ME), des regelmäßigen Fünfecks (EF) und des regelmäßigen Zehnecks (FM) mit dem gegebenen Umkreisradius r.

Konstruktion mit Zirkel und Lineal bei gegebener Seitenlänge

Mit Anwendung des Goldenen Schnitts, äußere Teilung

1. Zeichne eine Strecke AB, welche die Länge der vorgegebenen Seite des Fünfecks hat.
2. Verlängere die Strecke ab dem Punkt A um ca. drei Viertel der Strecke AB.
3. Zeichne einen Kreisbogen um den Punkt B mit dem Radius AB.
4. Zeichne einen Kreisbogen um den Punkt A mit dem Radius AB, es ergibt sich der Schnittpunkt F.
5. Fälle ein Lot von Punkt F auf die Strecke AB mit Fußpunkt G.
6. Zeichne eine Parallele zur Strecke FG ab dem Punkt A bis über den Kreisbogen um Punkt A, es ergibt sich der Schnittpunkt H.
7. Zeichne einen Kreisbogen um den Punkt G mit dem Radius GH bis zur Verlängerung der Strecke AB, es ergibt sich der Schnittpunkt J.
8. Zeichne einen Kreisbogen um den Punkt B mit dem Radius BJ bis über die Senkrechte, die durch den Punkt F geht, es ergeben sich die Schnittpunkte D auf der Senkrechten und E mit dem Kreisbogen um Punkt A.
9. Zeichne einen Kreisbogen um den Punkt D mit dem Radius BA, bis er den Kreisbogen um Punkt B schneidet, es ergibt sich der Schnittpunkt C.
10. Verbinde die Punkte B-C-D-E-A, somit ergibt sich das regelmäßige Fünfeck.

Fazit

Wie in der Konstruktion bei gegebenem Umkreis, ist auch hier der Goldene Schnitt der maßgebende Baustein.

Für den Vergleich der Konstruktionsvarianten sind die Punktebezeichnungen mit Indizes ergänzt: u für die Konstruktion mit gegebenem Umkreis, s für die Konstruktion mit gegebener Seitenlänge.

1. Seite des Fünfecks:
   ${\displaystyle {\overline {E_{u}F_{u}}}\;{\widehat {=}}\;{\overline {A_{s}B_{s}}}}$
2. Radius für den Goldenen Schnitt:
   ${\displaystyle {\overline {D_{u}E_{u}}}\;{\widehat {=}}\;{\overline {G_{s}H_{s}}}}$
3. Streckenverhältnisse des Goldenen Schnitts:
   ${\displaystyle \Phi ={\frac {\overline {A_{u}F_{u}}}{\overline {A_{u}M_{u}}}}={\frac {\overline {A_{u}M_{u}}}{\overline {M_{u}F_{u}}}}\;\;\;=\;\;\;{\frac {\overline {B_{s}J_{s}}}{\overline {A_{s}B_{s}}}}={\frac {\overline {A_{s}B_{s}}}{\overline {A_{s}J_{s}}}}\;\;\;=\;\;\;{\frac {1+{\sqrt {5}}}{2}}\approx 1{,}618}$

Papierfaltung

Durch Zusammenziehen eines aus einem Papierstreifen geschlungenen Überhandknotens nimmt dieser die Form eines regulären Fünfecks an.

• 
  Bild 4
  Falten der ersten Faltlinie ${\displaystyle \mathrm {F_{1}} }$
• 
  Bild 5
  Falten der zweiten Faltlinie ${\displaystyle \mathrm {F_{2}} }$
• 
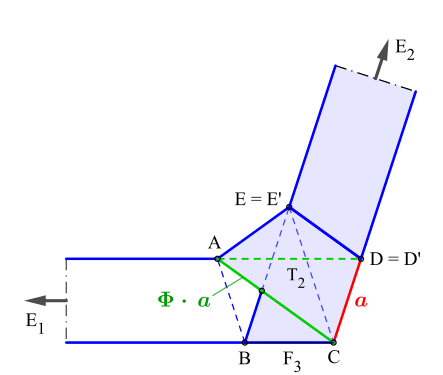  Bild 6
  Falten der dritten und letzten Faltlinie ${\displaystyle \mathrm {F_{3}} }$, Streifenende ${\displaystyle \mathrm {E_{2}} }$ zwischen dem Streifenende ${\displaystyle \mathrm {E_{1}} }$ und dem Trapez ${\displaystyle \mathrm {T_{2}} }$ durchgezogen

Polyeder mit regelmäßigen Fünfecken

Das Dodekaeder ist der einzige der platonischen Körper, der regelmäßige Fünfecke als Seitenflächen hat. Auch einige archimedische Körper enthalten regelmäßige Fünfecke, nämlich das Ikosidodekaeder, der Ikosaederstumpf, das Rhombenikosidodekaeder und das abgeschrägte Dodekaeder.

• 
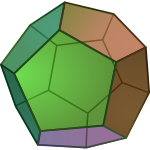  Dodekaeder
• 
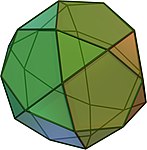  Ikosidodekaeder
• 
  Ikosaederstumpf (Fußballkörper)
• 
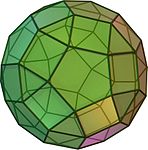  Rhombenikosidodekaeder
• 
  Abgeschrägtes Dodekaeder

Vorkommen

Natur

Sowohl die Okra als auch die Sternfrucht hat im Querschnitt die Form eines Fünfecks. Die Blüten der Prunkwinde sind ebenfalls fünfeckig ausgebildet. Auch Seesterne und Schlangensterne weisen eine fünfstrahlige Symmetrie auf. Näherungsweise trifft dies auch für die Blätter des Amerikanischen Amberbaums zu. Viele cyclische Verbindungen enthalten eine Fünfringstruktur (etwa Cyclopentan, γ-Butyrolacton, Furan, Furanosen etc.).

Architektur und Festungsbau

Der Grundriss einer neuzeitlichen bastionierten Festung hat häufig die Form eines Fünfecks. So sind regelmäßige Fünfecke die vollständig wieder aufgebaute Festung Bourtange in den Niederlanden sowie Nyenschanz (heute in St. Petersburg), die Zitadelle von Jaca, die Zitadelle von Pamplona, die Festung Dömitz, die Zitadelle von Turin, die Zitadelle von ’s-Hertogenbosch, die Zitadelle von Straßburg, die Zitadelle von Amiens, die 1598 abgebrochene Zitadelle von Vitry-le-François von Girolamo Marini, die verschwundene Zitadelle von Antwerpen, die Zitadelle von Doullens (Picardie, nur in Teilen auf regelmäßigem Grundriss), die Zitadelle von Lille, das Harburger Schloss, die Zitadelle Vechta, die Zitadelle von Münster, das Fort Nieuw-Amsterdam, das Kastell von Kopenhagen, Tilbury Fort in Essex östlich von London, die Festung auf der Insel Poel in Mecklenburg, die Höhenfestung Wülzburg bei Weißenburg in Bayern und die Festung Goryōkaku in Japan. Die Stadt Sathmar im heutigen Rumänien besaß eine fünfeckige Festung.

Den Typ des befestigten Palasts (Palazzo in fortezza) auf regelmäßig fünfeckigem Grundriss verkörpern die Villa Farnese in Caprarola (Provinz Viterbo, Italien), die Schlösser Krzyżtopór und Nowy Wiśnicz sowie die Befestigungen von Schloss Łańcut in Polen.

Der Hauptsitz des Verteidigungsministeriums der Vereinigten Staaten in Washington, D.C. wird wegen seines Grundrisses in Form des regelmäßigen Fünfecks Pentagon genannt.

Jeweils ein Fünfeck liegt Kirchengebäuden wie der Corvinuskirche in Hannover, der Dietrich-Bonhoeffer-Kirche (Köln-Lindenthal), der Kirche St. Michael in Detmold (Westfalen), der Kirche St. Markus in Recklinghausen, der Kirche Mariä Himmelfahrt (Irlbach) oder der Wallfahrtskirche Zelená Hora in der Tschechischen Republik zugrunde.

Auf fünfeckigem Querschnitt erheben sich Turmbauten wie der stählerne Verkehrsturm am Potsdamer Platz, der ehemalige Marinesignalturm Kiel, der aus Holz gefertigte Aussichtsturm auf der Hohenmirsberger Platte oder das Siegesdenkmal in Bangkok.

Der Fünfeckige Stein ist ein Grenzstein in Niederösterreich.

• 
  Zitadelle von Lille
• 
  Grundriss des Palazzo Farnese in Caprarola
• 
  Schloss Krzyżtopór
• 
  Festung auf der Insel Poel
• 
  Satellitenaufnahme des Pentagons
• 
  Goryōkaku

Kunst

Jacques Ozanam fertigte im Jahr 1699 einen Kupferstich an, in dem er u. a. die Konstruktion eines Fünfeck zeigt, das ein gegebenes gleichseitiges Dreieck umschließt.

Ozanams Ansatz zur Konstruktion des Fünfecks

Der halbe Innenwinkel eines regelmäßigen Fünfecks beträgt ${\displaystyle 54^{\circ }}$. Subtrahiert man von diesem den halben Innenwinkel ${\displaystyle 30^{\circ }}$ des gleichseitigen Dreiecks, ergibt sich der Winkel ${\displaystyle 24^{\circ }}$ zwischen dem Schenkel des Dreiecks und der Seite des Fünfecks.

Die Winkel ${\displaystyle 54^{\circ }}$, ${\displaystyle 30^{\circ }}$ und ${\displaystyle 24^{\circ }}$ haben den gemeinsamen Teiler ${\displaystyle 6}$. Dies bedeutet, der halbe Innenwinkel ${\displaystyle 54^{\circ }}$ des Fünfecks setzt sich aus ${\displaystyle 9}$ gleichen Teilen zu je ${\displaystyle 6^{\circ }}$ zusammen. Daraus folgt: Auf den halben Innenwinkel ${\displaystyle 30^{\circ }}$ des Dreiecks entfallen ${\displaystyle 5}$ bzw. auf den Winkel ${\displaystyle 24^{\circ }}$ zwischen dem Schenkel des Dreiecks und der Seite des Fünfecks entfallen ${\displaystyle 4}$ solcher Teile.

Vorgehensweise

Ausgehend vom gleichseitigen Dreieck ${\displaystyle ABC}$, zeichnet man zuerst dessen Höhe ${\displaystyle {\overline {AD}}}$ ein und schlägt anschließend einen Kreisbogen um den Punkt ${\displaystyle A}$ mit einem Radius etwas kleiner, als die halbe Höhe ${\displaystyle {\overline {AD}}}$; die Schnittpunkte sind ${\displaystyle O}$, ${\displaystyle D'}$ (Teilungspunkt ${\displaystyle 5}$) und ${\displaystyle O'}$. Es folgt die Konstruktion des Teilungspunktes ${\displaystyle 2}$ für den Winkel ${\displaystyle D'A\;2=18^{\circ }}$. Das Konstruktionsprinzip des Winkels ${\displaystyle 18^{\circ }}$ eines Fünfecks, ist auch in Dreiteilung des Winkels, Klassisches Problem (Bild) dargestellt. Die Teilungspunkte ${\displaystyle 1}$ und ${\displaystyle 3}$ sind für die Lösung nicht erforderlich, sie dienen lediglich der Verdeutlichung. Nach dem Eintragen des Teilungspunktes ${\displaystyle 4=N}$ mithilfe des Kreisbogens ${\displaystyle O\;2}$, wird ein Kreisbogen um ${\displaystyle O}$ mit Radius ${\displaystyle {\overline {ON}}}$ gezogen bis sich beide Kreisbögen in ${\displaystyle E}$ schneiden; dabei ergibt sich der Winkel ${\displaystyle NAE=48^{\circ }}$. Nun wird der Punkt ${\displaystyle H}$ mithilfe der Sehne ${\displaystyle {\overline {OE}}}$ ab ${\displaystyle O'}$ markiert.

Es geht weiter mit einem Kreisbogen um ${\displaystyle C}$ mit Radius ${\displaystyle {\overline {AD'}}}$; Schnittpunkt ist ${\displaystyle M}$. Das Übertragen des Winkels ${\displaystyle NAE=48^{\circ }}$ mithilfe der Sehne ${\displaystyle |EN|}$ auf den Kreisbogen um ${\displaystyle C}$ ab ${\displaystyle M}$ schließt sich an; Schnittpunkt ist ${\displaystyle K}$. Eine Halbgerade ab ${\displaystyle A}$ durch ${\displaystyle E}$ und eine zweite ab ${\displaystyle C}$ durch ${\displaystyle K}$ schneiden sich im Eckpunkt ${\displaystyle F}$ des entstehenden Fünfecks. Auf die gleiche Art und Weise – spiegelbildlich zur Höhe ${\displaystyle {\overline {AD}}}$ – ergibt sich der Eckpunkt ${\displaystyle I}$. Mithilfe der Mittelsenkrechten der Strecke ${\displaystyle {\overline {AF}}}$ erhält man den Mittelpunkt des Umkreises für das Fünfeck. Nach dem Ziehen des Umkreises werden die Strecken ${\displaystyle {\overline {FC}}}$ und ${\displaystyle {\overline {IB}}}$ bis zum Umkreis verlängert; dabei werden die beiden letzten Eckpunkte ${\displaystyle G}$ bzw. ${\displaystyle P}$ des Fünfecks generiert. Die abschließende Verbindung des Eckpunktes ${\displaystyle G}$ mit ${\displaystyle P}$ vollendet das gesuchte Fünfeck.

Siehe auch

• Fünfeck nach dem Satz von Mascheroni, allein mit einem Zirkel erstellt
• Parkettierung mit Fünfecken
• Goldener Schnitt

Weblinks

Commons: Regular pentagons – Sammlung von Bildern, Videos und Audiodateien

Commons: Fünfeck – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Fünfeck – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Beweisarchiv: Fünfeck – Lern- und Lehrmaterialien

Einzelnachweise

1. ↑ C. Stanley Ogilvy: Unterhaltsame Geometrie. Kapitel 9: Der Goldene Schnitt – 9.1 Das Pentagramm. Vieweg+Teubner Verlag, Wiesbaden 1984, ISBN 3-528-28314-9, S. 76–77, doi:10.1007/978-3-663-00104-1_10.