Mètrica de Poincaré

En matemàtiques, la mètrica de Poincaré, anomenada així en honor del matemàtic i físic francès d'Henri Poincaré, és el tensor mètric que descriu una superfície bidimensional de curvatura negativa constant. És la mètrica natural comunament utilitzada en una varietat de càlculs en geometria hiperbòlica o superfícies de Riemann.

Hi ha tres representacions equivalents comunament utilitzades en la geometria hiperbòlica bidimensional:

• El model de semiplà de Poincaré, que defineix un model d'espai hiperbòlic al semiplà superior.
• El model de disc de Poincaré defineix un model d'espai hiperbòlic al disc unitat. El disc i el semiplà superior estan relacionats per un mapa conforme, i les isometries es donen per transformacions de Möbius.
• Una tercera representació es troba al disc perforat, on s'expressen de vegades les relacions per als q-anàlegs.

A continuació es revisen aquests diversos formularis.

Visió general de mètriques sobre superfícies de Riemann

Una mètrica en el pla complex es pot expressar generalment en la forma

${\displaystyle ds^{2}=\lambda ^{2}(z,{\overline {z}})\,dz\,d{\overline {z}}}$

on λ és una funció real i positiva de ${\displaystyle z}$ i ${\displaystyle {\overline {z}}}$. La longitud d'una corba γ en el pla complex es donat per

${\displaystyle l(\gamma )=\int _{\gamma }\lambda (z,{\overline {z}})\,|dz|}$

L'àrea d'un subconjunt del pla complex es dona per

${\displaystyle {\text{Area}}(M)=\int _{M}\lambda ^{2}(z,{\overline {z}})\,{\frac {i}{2}}\,dz\wedge d{\overline {z}}}$

on ${\displaystyle \wedge }$ és el producte exterior utilitzat per construir la forma volum. El determinant de la mètrica és igual a ${\displaystyle \lambda ^{4}}$, de manera que l'arrel quadrada del determinant és ${\displaystyle \lambda ^{2}}$. La forma volum euclidià al pla és ${\displaystyle dx\wedge dy}$ i així s'obté

${\displaystyle dz\wedge d{\overline {z}}=(dx+i\,dy)\wedge (dx-i\,dy)=-2i\,dx\wedge dy.}$

La funció ${\displaystyle \Phi (z,{\overline {z}})}$ es diu que és el potencial de la mètrica si

${\displaystyle 4{\frac {\partial }{\partial z}}{\frac {\partial }{\partial {\overline {z}}}}\Phi (z,{\overline {z}})=\lambda ^{2}(z,{\overline {z}}).}$

L'operador de Laplace-Beltrami és donat per

${\displaystyle \Delta ={\frac {4}{\lambda ^{2}}}{\frac {\partial }{\partial z}}{\frac {\partial }{\partial {\overline {z}}}}={\frac {1}{\lambda ^{2}}}\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}\right).}$

La curvatura gaussiana de la mètrica és donada per

${\displaystyle K=-\Delta \log \lambda .\,}$

Aquesta curvatura és la meitat de la curvatura escalar de Ricci.

Les isometries conserven angles i longituds d'arc. A les superfícies de Riemann, les isometries són idèntiques als canvis de coordenades, és a dir, tant l'operador de Laplace-Beltrami com la curvatura són invariants sota isometries. Així, per exemple, fem que S sigui una superfície de Riemann amb mètrica ${\displaystyle \lambda ^{2}(z,{\overline {z}})\,dz\,d{\overline {z}}}$ i T sigui una superfície de Riemann amb mètrica ${\displaystyle \mu ^{2}(w,{\overline {w}})\,dw\,d{\overline {w}}}$. Llavors, un mapa

${\displaystyle f:S\to T\,}$

amb ${\displaystyle f=w(z)}$és una isometria si i només si és conforme i si

${\displaystyle \mu ^{2}(w,{\overline {w}})\;{\frac {\partial w}{\partial z}}{\frac {\partial {\overline {w}}}{\partial {\overline {z}}}}=\lambda ^{2}(z,{\overline {z}})}$.

Aquí, l'exigència que el mapa sigui conforme no és més que la declaració

${\displaystyle w(z,{\overline {z}})=w(z),}$

això és,

${\displaystyle {\frac {\partial }{\partial {\overline {z}}}}w(z)=0.}$

Element mètric i de volum en el pla de Poincaré

El tensor mètric de Poincaré al model de semiplà de Poincaré es dona en el semiplà superior ${\displaystyle H}$ com

${\displaystyle ds^{2}={\frac {dx^{2}+dy^{2}}{y^{2}}}={\frac {dz\,d{\overline {z}}}{y^{2}}}}$

on escrivim ${\displaystyle dz=dx+i\,dy.}$Aquest tensor mètric és invariant sota l'acció de SL(2,R). És a dir, si escrivim

${\displaystyle z'=x'+iy'={\frac {az+b}{cz+d}}}$

per a ${\displaystyle ad-bc=1}$ llavors podem resoldre-ho

${\displaystyle x'={\frac {ac(x^{2}+y^{2})+x(ad+bc)+bd}{|cz+d|^{2}}}}$

i

${\displaystyle y'={\frac {y}{|cz+d|^{2}}}.}$

Les transformacions infinitesimals com

${\displaystyle dz'={\frac {dz}{(cz+d)^{2}}}}$

i així

${\displaystyle dz'd{\overline {z}}'={\frac {dz\,d{\overline {z}}}{|cz+d|^{4}}}}$

per tant, deixant clar que el tensor mètric és invariant sota SL(2,R).

L'element de volum invariant es dona per

${\displaystyle d\mu ={\frac {dx\,dy}{y^{2}}}.}$

La mètrica és donada per

${\displaystyle \rho (z_{1},z_{2})=2\tanh ^{-1}{\frac {|z_{1}-z_{2}|}{|z_{1}-{\overline {z_{2}}}|}}}$

${\displaystyle \rho (z_{1},z_{2})=\log {\frac {|z_{1}-{\overline {z_{2}}}|+|z_{1}-z_{2}|}{|z_{1}-{\overline {z_{2}}}|-|z_{1}-z_{2}|}}}$

per a ${\displaystyle z_{1},z_{2}\in \mathbb {H} .}$

Una altra forma interessant de la mètrica es pot donar en termes de la relació creuada. Tenint en compte quatre punts ${\displaystyle z_{1},z_{2},z_{3}}$ i ${\displaystyle z_{4}}$en el pla complex compactat ${\displaystyle {\hat {\mathbb {C} }}=\mathbb {C} \cup \{\infty \},}$la relació creuada es defineix per

${\displaystyle (z_{1},z_{2};z_{3},z_{4})={\frac {(z_{1}-z_{3})(z_{2}-z_{4})}{(z_{1}-z_{4})(z_{2}-z_{3})}}.}$

Llavors la mètrica es dona per

${\displaystyle \rho (z_{1},z_{2})=\log \left(z_{1},z_{2};z_{1}^{\times },z_{2}^{\times }\right).}$

Aquí, ${\displaystyle z_{1}^{\times }}$ i ${\displaystyle z_{2}^{\times }}$ són els punts finals, en la línia de nombres reals, de l'enllaç geodèsic ${\displaystyle z_{1}}$ i ${\displaystyle z_{2}}$. Aquests estan numerats de manera que ${\displaystyle z_{1}}$es troba entre ${\displaystyle z_{1}^{\times }}$ i ${\displaystyle z_{2}}$.

Les geodèsiques d'aquest tensor mètric són arcs circulars perpendiculars a l'eix real (mig cercle l'origen del qual es troba a l'eix real) i línies verticals rectes que acaben en l'eix real.

Mapa conforme del pla al disc

Al semiplà superior es pot mapejar de manera conforme al disc unitat amb la transformació de Möbius

${\displaystyle w=e^{i\phi }{\frac {z-z_{0}}{z-{\overline {z_{0}}}}}}$

on w és el punt del disc unitat que correspon al punt z al semimplà superior. En aquest mapatge, la constant z₀ pot ser qualsevol punt del semiplà superior; es mapejarà al centre del disc. L'eix real ${\displaystyle \Im z=0}$mapeja a la vora del disc d'unitat ${\displaystyle |w|=1.}$ El nombre real constant ${\displaystyle \phi }$ es pot utilitzar per girar el disc per una quantitat fixa arbitrària.

El mapatge canònic és

${\displaystyle w={\frac {iz+1}{z+i}}}$

que porta i al centre del disc, i 0 a la part inferior del disc.

Element mètric i de volum al disc de Poincaré

El tensor mètric de Poincaré al model de disc de Poincaré es dona al disc unitat obert

${\displaystyle U=\left\{z=x+iy:|z|={\sqrt {x^{2}+y^{2}}}<1\right\}}$

per

${\displaystyle ds^{2}={\frac {4(dx^{2}+dy^{2})}{(1-(x^{2}+y^{2}))^{2}}}={\frac {4dz\,d{\overline {z}}}{(1-|z|^{2})^{2}}}.}$

L'element de volum es dona per

${\displaystyle d\mu ={\frac {4dx\,dy}{(1-(x^{2}+y^{2}))^{2}}}={\frac {4dx\,dy}{(1-|z|^{2})^{2}}}.}$

La mètrica de Poincaré és donada per

${\displaystyle \rho (z_{1},z_{2})=2\tanh ^{-1}\left|{\frac {z_{1}-z_{2}}{1-z_{1}{\overline {z_{2}}}}}\right|}$

per a ${\displaystyle z_{1},z_{2}\in U.}$

Les geodèsiques d'aquest tensor mètric són arcs circulars on els extrems són ortogonals al límit del disc. Els fluxos geodèsics sobre el disc de Poincaré són fluxos d'Anosov (aquest article desenvolupa la notació per a aquests fluxos).

El model de disc perforat

Un segon mapatge comú del semiplà superior a un disc és el q-mapatge

${\displaystyle q=\exp(i\pi \tau )}$

on q és el nome i τ és la relació de semiperíode:

${\displaystyle \tau ={\frac {\omega _{2}}{\omega _{1}}}}$ .

A la notació de les seccions anteriors, τ és la coordenada del semiplà superior ${\displaystyle \Im \tau >0}$. El mapatge és al disc perforat, perquè el valor q=0 no està a la imatge del mapa.

La mètrica de Poincaré al semiplà superior indueix una mètrica al q-disc

${\displaystyle ds^{2}={\frac {4}{|q|^{2}(\log |q|^{2})^{2}}}dq\,d{\overline {q}}}$

El potencial de la mètrica és

${\displaystyle \Phi (q,{\overline {q}})=4\log \log |q|^{-2}}$

• 
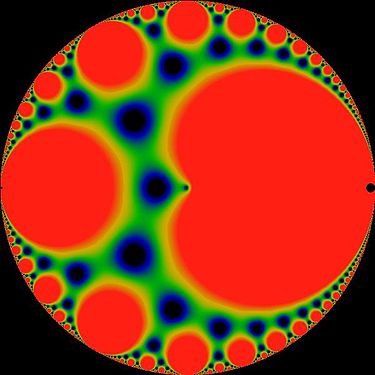  J-invariant en coordenades de disc perforat; és a dir, com a funció del nome
• 
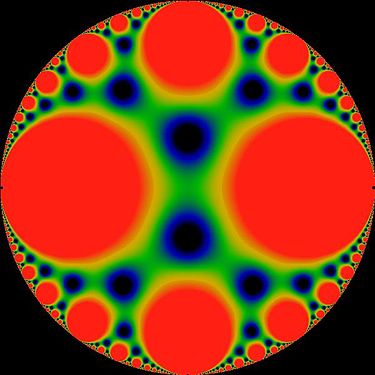  J-invariant en coordenades de disc de Poincaré; tingueu en compte que aquest disc es gira de 90 graus a partir de les coordenades canòniques que es proporcionen en aquest article

Lema de Schwarz

La mètrica de Poincaré és la disminució de la distància en funcions harmòniques. Aquesta és una extensió del lema de Schwarz, anomenat teorema de Schwarz-Ahlfors-Pick.

Referències

• Hershel, M. Farkas; Irwin, Kra. Riemann Surfaces (en anglès). Nova York: Springer-Verlag, 1980. ISBN 0-387-90465-4. 
• Jurgen, Jost. «Secció 2.3». A: Compact Riemann Surfaces (en anglès). Nova York: Springer-Verlag, 2002. ISBN 3-540-43299-X. 
• Katok, Svetlana. Fuchsian Groups (en anglès). Chicago: University of Chicago Press, 1992. ISBN 0-226-42583-5. 

Vegeu també

• Geodèsica principal
• Grup Fuchsià
• Grup Kleinià
• Model Fuchsià
• Model Kleinià