Espai hiperbòlic

En matemàtiques, l'espai hiperbòlic és un espai, introduït al segle xix pels matemàtics János Bolyai i Nikolai Ivànovitx Lobatxevski de manera independent, que es defineix en una geometria no euclidiana anomenada geometria hiperbòlica. Es tracta, juntament amb la geometria el·líptica, de l'exemple més important de la geometria no euclidiana.

Els models

L'espai hiperbòlic té una dimensió arbitrària n {\displaystyle n} i se simbolitza com H n {\displaystyle \mathbb {H} ^{n}} . Hi ha tot un seguit de models equivalents que el representen, com el disc de Poincaré, el semiespai de Poincaré o el model de l'hiperboloide. Igual que en el cas de la geometria euclidiana, els espais més estudiats són el pla hiperbòlic H 2 {\displaystyle \mathbb {H} ^{2}} i l'espai hiperbòlic tridimensional H 3 {\displaystyle \mathbb {H} ^{3}} .

El disc de Poincaré

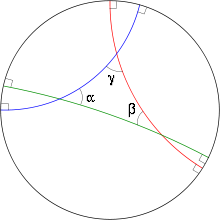
Les tres línies incidents del model del disc. Una línia és un arc de circumferència (o segment) ortogonal al límit del disc.

En el model del disc de Poincaré, l'espai hiperbòlic és la bola n {\displaystyle n} -dimensional:

B n = { x ∈ R n   |   | x | < 1 } . {\displaystyle B^{n}=\{x\in \mathbb {R} ^{n}\ |\ |x|<1\}.}

Per n = 2 {\displaystyle n=2} és el cercle de radi unitari centrat en l'origen de la pla cartesià.

En el disc de Poincaré una línia és un arc de circumferència, o un segment, que creua ortogonalment el límit o vora ∂ B n {\displaystyle \partial B^{n}} de la bola B n {\displaystyle B^{n}} en dos punts. Dues "línies" que es tallen en un punt formen un angle, i la seva obertura és igual al de l'angle format per les tangents.

Model del semiespai

En el model del semiespai de Poincaré l'espai hiperbòlic és el semiespai

{ ( x 1 , … , x n ) ∈ R n   |   x n > 0 } . {\displaystyle \{(x_{1},\ldots ,x_{n})\in \mathbb {R} ^{n}\ |\ x_{n}>0\}.}

Igual que en el model del disc, les línies hiperbòliques són els arcs de circumferència i les línies ortogonals al límit. En aquest model, el límit és l'hiperplà horitzontal x n = 0 {\displaystyle x_{n}=0} .

Model de l'hiperboloide

En el model de l'hiperboloide l'espai hiperbòlic és l'hiperboloide

H = { ( x 1 , … , x n + 1 ) ∈ R n + 1   |   x 1 2 + … + x n 2 − x n + 1 2 = − 1 , x n + 1 > 0 } . {\displaystyle H={\big \{}(x_{1},\ldots ,x_{n+1})\in \mathbb {R} ^{n+1}\ {\big |}\ x_{1}^{2}+\ldots +x_{n}^{2}-x_{n+1}^{2}=-1,x_{n+1}>0{\big \}}.}

En aquest model, una línia vindrà donada per la intersecció de H {\displaystyle H} amb un pla que passi per l'origen de R n + 1 {\displaystyle \mathbb {R} ^{n+1}} . En aquest context, és útil definir R n + 1 {\displaystyle \mathbb {R} ^{n+1}} una estructura espaitemps de Minkowski, és a dir, el producte escalar amb signatura ( n , 1 ) {\displaystyle (n,1)} :

ϕ ( ( x 1 , … , x n + 1 ) , ( y 0 , … , y n + 1 ) ) = x 1 y 1 + … + x n y n − x n + 1 y n + 1 . {\displaystyle \phi {\big (}(x_{1},\ldots ,x_{n+1}),(y_{0},\ldots ,y_{n+1}){\big )}=x_{1}y_{1}+\ldots +x_{n}y_{n}-x_{n+1}y_{n+1}.}

Tots els x {\displaystyle x} amb ϕ ( x , x ) = − 1 {\displaystyle \phi (x,x)=-1} tenen dos components connexos, un dels quals (el de dalt, amb x n + 1 > 0 {\displaystyle x_{n+1}>0} ) és l'hiperboloide H {\displaystyle H} . La distància entre dos punts P {\displaystyle P} i Q {\displaystyle Q} en H {\displaystyle H} es defineix com

d ( P , Q ) = arccosh ⁡ ( ϕ ( P , Q ) ) . {\displaystyle d(P,Q)=\operatorname {arccosh} (\phi (P,Q)).}

Referències

  • Ratcliffe, John G., Foundations of hyperbolic manifolds, Nova York, Berlin. Springer-Verlag, 1994.
  • Reynolds, William F. (1993) Hyperbolic Geometry on a Hyperboloid, American Mathematical Monthly, 100:442-455.
  • Wolf, Joseph A. Spaces of constant curvature, 1967. pàgina 67.

Vegeu també