Equació de Tsiolkovski

L'equació de Tsiolkovski o equació del coet ideal descriu el moviment de vehicles que segueixen el principi bàsic d'un coet: un dispositiu que aplicar-se a si mateix acceleració (un empenyiment) mitjançant l'expulsió de part de la seva massa a altes velocitats i moure's mitjançant la conservació de la quantitat de moviment. L'equació relaciona el delta-v (el màxim increment de velocitat d'un coet si no actua cap altra força externa) amb l'impuls específic (velocitat dels gasos a la sortida respecte al coet) i les masses inicial i final del coet.

L'expressió de Tsiolkovski expressa que per a qualsevol maniobra o viatge que inclogui maniobres:

${\displaystyle \Delta v=v_{\text{e}}\ln {\frac {m_{0}}{m_{1}}}}$

on:

${\displaystyle m_{0}}$ és la massa total inicial, incluint el propergol,

${\displaystyle m_{1}}$ és la massa final sense propergol, també anomenat massa seca.

${\displaystyle v_{\text{e}}}$ és la velocitat dels gasos a la sortida respecte al coet,

${\displaystyle \Delta v\ }$ és delta-v - el màxim canvi de velocitat del vehicle (sense que actuiin forces externes),

${\displaystyle \ln }$ és la funció del logaritme natural.

L'equació rep el nom del científic rus Konstantín Tsiolkovski que la va trobar i publicar independentment en el seu treball de 1903.^[1] L'equació havia estat trobada abans pel matemàtic britànic William Moore.^[2]

Història

Aquesta equació va ser deduïda de manera independent per Konstantín Tsiolkovski cap al final del segle xix és sovint coneguda com l'equació del coet. Tanmateix, un pamflet descobert recentment anomenat Un tractat sobre el moviment dels coets (A Treatise on the Motion of Rockets en anglès) del matemàtic britànic William Moore^[2] mostra que una derivació prèvia d'una equació semblant ja apareixia a la Royal Military Academy de Woolwich el 1813,^[3] i s'utilitzava en la recerca en armes.

Mentre que la derivació de l'equació del coet és un exercici de càlcul senzill, Tsiolkovski té l'honor de ser el primer a aplicar-la per respondre la pregunta de si els coets podien arribar a les velocitats necessàries per al viatge espacial.

Derivació

Considerant el següent sistema:

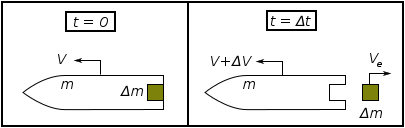
En la següent derivació, quan es digui el coet s'entendrà el coet i tot el propergol no cremat.

La segona llei de Newton relaciona les forces externes (${\displaystyle F_{i}}$) amb el moment lineal (${\displaystyle P}$) de tot el sistema, inclòs el coet i els gasos d'escapament de la següent manera:

${\displaystyle \sum F_{i}=\lim _{\Delta t\to 0}{\frac {P_{2}-P_{1}}{\Delta t}}}$

on ${\displaystyle P_{1}\,}$ és el moment lineal del sistema quan t=0 (quan només es mou el coet de massa m + Δm i velocitat V):

${\displaystyle P_{1}=\left({m+\Delta m}\right)V}$

i ${\displaystyle P_{2}\,}$ és el moment lineal del coet (de massa m i velocitat V + ΔV) més el dels gasos d'escapament (de massa Δm i velocitat V_e) en l'instant ${\displaystyle t=\Delta t\,}$ :

${\displaystyle P_{2}=m\left(V+\Delta V\right)+\Delta mV_{e}}$

i on, respecte a l'observador:

${\displaystyle V\,}$ és la velocitat del coet en el temps t=0

${\displaystyle V+\Delta V\,}$ és la velocitat del coet en el temps ${\displaystyle t=\Delta t\,}$

${\displaystyle V_{e}\,}$ és la velocitat dels gasos a la sortida (de la massa perduda pel coet durant el temps ${\displaystyle \Delta t\,}$)

${\displaystyle m+\Delta m\,}$ és la massa del coet en el temps t=0

${\displaystyle m\,}$ és la massa del coet en el temps ${\displaystyle t=\Delta t\,}$

La velocitat dels gasos a la sortida (${\displaystyle V_{e}}$) des del sistema de referència de l'observador està relacionat amb la velocitat dels gasos a la sortida des del sistema de referència del coet ${\displaystyle v_{e}}$ segons (ja que la velocitat va en la direcció negativaː

${\displaystyle V_{e}=V-v_{e}}$

Que, substituintː

${\displaystyle P_{2}-P_{1}=m\Delta V-v_{e}\Delta m\,}$

i, utilitzant ${\displaystyle dm=-\Delta m}$, ja que expulsar un ${\displaystyle \Delta m}$ positiu comporta una disminució en massa,

${\displaystyle \sum F_{i}=m{\frac {dV}{dt}}+v_{e}{\frac {dm}{dt}}}$

Si no hi ha forces externes llavors ${\displaystyle \sum F_{i}=0}$ (conservació del moment lineal) i

${\displaystyle m{\frac {dV}{dt}}=-v_{e}{\frac {dm}{dt}}}$

Assumint ${\displaystyle v_{e}\,}$ és constant, es pot integrar resultant:

${\displaystyle \Delta V\ =v_{e}\ln {\frac {m_{0}}{m_{1}}}}$

o, equivalentmentː

${\displaystyle m_{1}=m_{0}e^{-\Delta V\ /v_{e}}\qquad \qquad o\qquad \qquad m_{0}=m_{1}e^{\Delta V\ /v_{e}}\qquad \qquad o\qquad \qquad m_{0}-m_{1}=m_{1}(e^{\Delta V\ /v_{e}}-1)}$

on ${\displaystyle m_{0}}$ és la massa total inicial, inclòs el combustible, ${\displaystyle m_{1}}$ és la massat total final, i ${\displaystyle v_{e}}$ la velocitat dels gasos a la sortida respecte al coet (l'impuls específic, o, si es mesura en temps, el mateix multiplicat per l'acceleració de la gravetat terrestre).

El valor ${\displaystyle m_{0}-m_{1}}$ és la massa total de combustible expulsat, i llavors:

${\displaystyle M_{f}=1-{\frac {m_{1}}{m_{0}}}=1-e^{-\Delta V\ /v_{\text{e}}}}$

on ${\displaystyle M_{f}}$ és la fracció de massa (la raó entre la massa del propergol entre la massa inicial total).

Vegeu també

• Delta-v
• Impuls específic
• Propulsió espacial

Referències